3.4.15. Генератори прямокутних імпульсів

В колі додатного зворотного зв’язку генераторів прямокутної форми зазвичай використовуються резистори R₁, R₂, які задають значення коефіцієнта β його передавання (рис. 3.27.а) β= R₁/(R₁+R₂). Вихідна напруга такого генератора періодично змінюється між Двома значеннями напруги, що визначаються напругами насичення або ОП. Часи t₁ та t₂ перебування ОП в стані або визначаються сталою RC-ланки, коефіцієнтом передавання β кола ДЗЗ та значеннями напруг ,

(3.64)

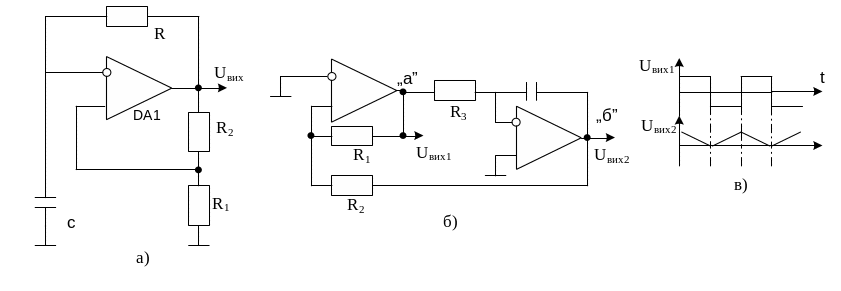
Рис.3.27 – схеми генераторів сигналів прямокутної та трикутної форми

(3.65)

Період Т генерованих імпульсів визначатиметься сумою часів t₁ і t₂ і за умови повної симетрії | |=| |

Т=1/f= t₁+t₂=2RCln(1+2 R₁/R₂). (3.66)

3.4.16. Генератори трикутних імпульсів

Найпростіша схема генератора трикутних імпульсів така ж, як і схема генератора прямокутних імпульсів (рис. 3.27.а). Однак, значення коефіцієнта передавання β кола ДЗЗ менша, ніж в генераторі прямокутних імпульсів, що дає можливість уникнути насичення ОП. Розрахунок параметрів генератора трикутної напруги здійснюється за формулами (3.63), (3.64) за умови, що значення напруг перемикання напряму протікання зарядного струму конденсатора С менше від значення напруги насичення ОП , . За умови використання двох ОП, один з яких DA1 є компаратором, а другий DA2 інвертором, є можливість у точці «а» отримувати сигнал напруги прямокутної форми, а у точці «б» - трикутної форми (рис. 3.27.б, рис. 3.27.в). Амплітуда вихідного трикутного сигналу визначається відношенням опорів резисторів R₂/R₁, а частота – сталою часу RC-ланки.

4. Інтегральні ацп та цап

4.1. Аналого-цифрове перетворення

Як було зазначено вище, основним та найважливішим вузлом будь-яких цифрових вимірювальних засобів є АЦП, від метрологічних параметрів якого прямо залежать параметри вимірювального засобу в цілому. При аналого-цифровому перетворенні у загальному випадку виконуються операції дискретизації вимірюваної величини в часі, квантування її за рівнем та кодування у певній системі числення.

У дискретизованому сигналі відсутні проміжні значення вхідного сигналу між мітками часу t_i та t_i+1. Завдяки цьому може втрачатися вимірювальна інформація про проміжні значення сигналу, тобто виникає похибка від дискретизації. Крім того, завжди існує певна, не нульова, тривалість аналого-цифрового перетворення сигналу, яка залежить від використовуваного методу перетворення та швидкодії елементної бази АЦП [].

Тому під час дискретизації сигналу можна розглядати дві часові характеристики цього процесу: (1) – часовий інтервал поміж між почерговими вимірюваннями сигналу (при сталому часі його називають періодом дискретизації сигналу T_д=t_i+1-t_i); і (2) – інтервал часу T_а/ц аналого-цифрового перетворення сигналу – час, який необхідно затратити, щоб отримати один цифровий результат вимірювання сигналу. Відповідно до цього при цифрових вимірюваннях розглядають похибки двох різновидів (рис. 4.1):

1) похибка Т_ (t), що пов’язана зі зміною вимірюваного сигналу за час між окре­мими вибірками (інтервал дискретизації);

2) похибка _А / Ц(t), що пов’язана зі зміною сигналу за час його аналого-цифрового перетворення.

При відомому періоді дискретизації перша складова похибки однозначно залежить від властивостей зміни вимірюваного сигналу і способу наступного використання результатів його вимірювань [].

Якщо до отримання наступної вибірки Х_i+1 за поточне значення сигналу x(t) приймається стале значення, яке дорівнює значенню попередньої вибірки Х_i (відтворення сигналу подібною до сходинок функцією (рис. 4.2)), то найбільша похибка пропорційна до найбільшої швидкості зміни сигналу на проміжку t_i t<t_i+1 між почерговими вибірками

 _дс(Т_)    х(t) _maxT_.  (4.1)

Рис. 4.1. До похибок дискретизації при аналого-цифровому перетворенні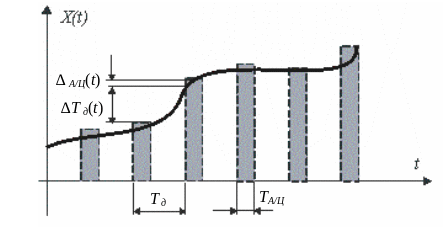

При гармонійному сигналі амплітудою x_м і частотою : х(t)_max = x_m, то максимальна похибка дискретизації не перевищує значення _дс(T_)  х_mT_.

Значення цієї похибки можна зменшити, якщо зачекати до моменту часу t_i+1 отримання наступної вибірки Х_i+1 і апроксимувати залежність зміни сигналу між почерговими вимірюваннями лінійною функцією (рис. 4.2).

В цьому випадку максимальне значення похибки залежить від максимальної другої похідної сигналу (при лінійній зміні сигналу похибка відсутня)

(4.2)

і для гармонійного сигналу, для якого x (t)_max =   ²x_m, максимальна динамічна похибка від дискретизації не перевищує значення .

Приклад. При цифровому вимірюванні значень змінної напруги частотою 50 Гц при частоті дискретизації T_д = 1 мс (20 значень за період) віднесені до амплітуди сигналу похибки дискретизації сигналу становлять _дс(Т_  / х_m_max  T_ = 250 1  10^3  0,314  31% при відтворенні східчастоподібною функцією і _дл(Т_) |x_mmax|  0,5(T_ / 2)²=  = 0,5(50 · 1  · 10^-3)²   0,012 = 1,2% – при відтворенні сигналу лінійною функцією.

Рис. 4.2. Похибка дискретизації при відтворенні сигналу лінійними функціями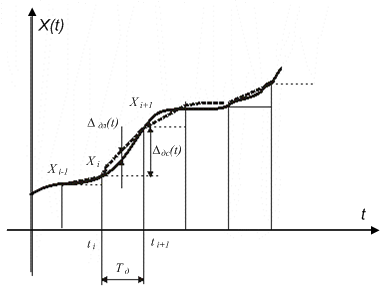

Як бачимо, усклад-нення способу відтворен-ня проміжних значень сигналу радикально змен-шує динамічну похибку від дискретизації.

Однак при цьому, для відтворення проміжних значень сигналу необхід-но здійснити затримку на інтервал часу рівний пері-оду дискретизації. Якщо результати вимі­рювань використовують для керування якимось процесом, то така затримка може бути небажаною або, навіть, недопустимою.