Сжатие «вручную» 2-х фрагментов данных c применением кодов Хаффмана

11. gdadafghggfghababahbagggabcdcdcahhggaghhhgacagca

Рассчитаем частоты появления символов алфавита:

g = 13/48 = 0,271

d = 4/48 = 0,083

a = 12/48 = 0,25

f = 2/48 = 0,042

h = 8/48 = 0,167

b = 4/48 = 0,083

c = 5/48 = 0,104

Сформируем дерево:

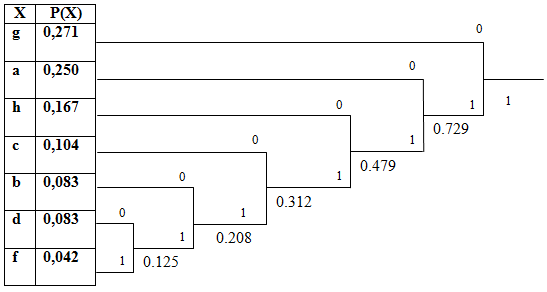
Код Хаффмана символов алфавита:

X	Code
g	0
a	10
h	110
c	1110
b	11110
d	111110
f	111111

Предположим, что входной поток был байт ориентированным, тогда

K_сж = 8/ (0,271∙1 + 0,250∙2 + 0,167∙3 + 0,104∙4 + 0,083∙5 + 0,083∙6 + 0,042∙6) = 8/ 2,853 = 2,804.

Сжатие считается эффективным.

10. faaadddddbbbccbaffbbbaabbabbbabbfcadcbfababadddab

Рассчитаем частоты появления символов алфавита:

a = 13/49 = 0,265

b = 18/49 = 0,367

c = 4/49 = 0,082

d = 9/49 = 0,184

f = 5/49 = 0,102

Сформируем дерево:

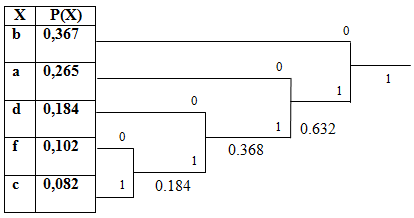
Код Хаффмана символов алфавита:

X	Code
b	0
a	10
d	110
f	1110
c	1111

Предположим, что входной поток был байт ориентированным, тогда

K_сж = 8/ (0,367∙1 + 0,265∙2 + 0,184∙3 + 0,102∙4 + 0,082∙4) = 8/ 2,185 = 3,661.

Сжатие считается эффективным.

Сжатие «вручную» фрагмента данных с применением алгоритмов rle, lzw и кодов Хаффмана

Исходная строка:

16. abaaabbccdabaacadb

Применение алгоритма RLE

Исходная строка будет закодирована следующим образом:

02ab3a2b2c03dab2a04cadb

Так как исходная строка занимала 18 байт, а кодированная – 23 байт, то достигается коэффициент сжатия K_сж = 18/23 = 0,783 < 1. Сжатие считается не эффективным.

Применение алгоритма LZW

a | b | a | aa | b | b | c | c | d | ab | aa | c | a | d | b

0 1 0 6 1 1 2 2 3 4 6 2 0 3 1

Номер слова	Слово	Номер слова	Слово
0	a	9	bc
1	b	10	cc
2	c	11	cd
3	d	12	da
4	ab	13	aba
5	ba	14	aac
6	aa	15	ca
7	aab	16	ad
8	bb	17	db

Сжатый поток состоит из ссылок:

0 1 0 6 1 1 2 2 3 4 6 2 0 3 1

Входной поток был байтовым, на каждую ссылку отводится тоже один байт, получаем коэффициент сжатия К_сж = 18/15 = 1,2 > 1. Сжатие считается эффективным.

Применение метода сжатия с использованием кода Хаффмана

Рассчитаем частоты появления символов алфавита:

a = 8/18 = 0,444

b = 5/18 = 0,278

c = 3/18 = 0,167

d = 2/18 = 0,111

Сформируем дерево:

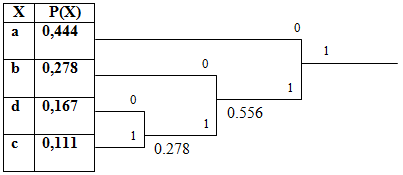
Код Хаффмана символов алфавита:

X	Code
a	0
b	10
d	110
c	111

Предположим, что входной поток был байт ориентированным, тогда

K_сж = 8/ (0,444∙1 + 0,278∙2 + 0,167∙3 + 0,111∙3) = 8/ 1,723 = 4,362.

Сжатие считается эффективным.

Вывод: Для данного примера наиболее эффективным является сжатие с применением кода Хаффмана.