§ 3. Додавання цілих невід'ємних чисел. Основні властивості додавання, їх наслідки.

Нагадаємо, що сумою або об'єднанням скінченних множин А, В, С, ..., К, що не мають спільних елементів, називається така множина S, яка містить всі елементи даних множин і не містить ніяких інших елементів:

S =А  В  С …К.

Сума скінченної кількості скінченних множин буде скінченною множиною.

Означення. Сумою натуральних чисел а, b, с, ..., k називається натуральне

число s, що є кількісною характеристикою множини S, яка є об'єднанням множин А, В, С, .... К. без спільних елементів, чисельність яких характеризується відповідно числами а, b, с, ..., k.

Числа а, b, с, ..., k називаються доданками, а операція одержання їх суми — дією додавання: а + b + с + ...+ k = s , якщо А  В  С …К = S, при умові, що всі попарні перерізи множин А, В, С, ..., К, є порожні множини.

Інакше п (А) + п (В) + ... п (К) == п (А  В  ... К), якщо А B = A С = .. =A K = B С= ••• =

Якщо одна з двох множин порожня, то, як зазначалося, об'єднанням цих двох множин буде друга з них: А   =  А=А. Об'єднання двох порожніх множин є порожня множина    = . Звідси випливає, що а + 0 = 0 + а = а; 0 + 0 = 0. Основні властивості додавання натуральних чисел розглянемо, зіставляючи їх з відповідними властивостями множин (які вже доводили).

1

Які б не були скінченні множини А, В, С, ..., К, без спільних елементів, завжди існує, причому єдина , скінчена множина S, що є їх об’єднанням:

(A, B, …,K  S ) (S = A  B  C …K)

Які б не були цілі невід’ємні числа a, b, c,…k, завжди існує ціле невід’ємне число s, причому єдине, яке є їх сумою :

(a, b, c,…kN₀ sN₀ ) (s = a + b + c +…+k )

. Існування і єдиністъ суми.

2

(A, B) (A  B = B  A ).

Означення об’єднання множин не передбачає порядку ( послідовності ) об’єднання множин - доданків.

Від перестановки доданків сума цілих невід’ємних чисел не змінюється:

(a, b N₀) (a + b = b + a ).

. Комутативний закон додавання (переставна властивість суми)

Цю властивість використовують ще з першого класу. На конкретних множинах (кубиках, олівцях, зошитах тощо) вчитель пояснює, що легше до 9 додати 2 (приєднанням по одиниці), ніж до 2 додавати 9, а кількість, наприклад, кубиків не зменшиться від того, чи до 9 кубиків, що стоять справа на планці дошки, приєднати 2 кубики, які стоять зліва, чи навпаки: 2 + 9 = 9 + 2.

У підручнику для першокласників вміщено таку цікаву задачу:

«В одному кутку приміщення лежало 9 ящиків, а в другому — один ящик. Потрібно скласти їх в один куток. Один учень швидко впорався із завданням: він переніс один ящик, поклав його до дев'яти. Другий же, навпаки, переніс всі ящики в куток, де лежав один ящик. Який з цих учнів поступив розумніше?»

3. Асоціативний закон додавання (сполучна властивість суми)

1. A  B  C = ( A  B )  C = A  (B  C);

2. A  B  C  D = ( A  B )  (C  D) = (A  B  C)  D = A  ( B  C  D)

1. (a, b, cN₀ ) (a + b + c )=(a +b ) + c = a+ (b+c);

2. (a, b, c, d N₀ ) ( a + b + c + d ) = ( a + b) + (c + d ) = ( a + b + c) + d = a + (b + c + d )

Сума цілих невід'ємних чисел не зміниться, якщо два або кілька доданків замінити їх сумою.

Доведення випливає з означення додавання множин

Наслідки із комутативного та асоціативного законів додавання:

а) Додавання числа до суми і суми до числа.

1) (а + b) + с = (а + с) + b = а + (b + с);

2) а + (b + с) = (а + b) + с =(а + с) + b.

Додати число до суми або суму до числа можна двома способами:

обчислити суму і до результату додати дане число або додати це число до одного з доданків, а до результату додати другий доданок.

Правила додавання суми до числа і числа до суми розглядаються ще в першому класі, вони є теоретичною основою додавання одно­цифрового числа до двоцифрового, і навпаки. Як додати, наприклад, до 15 число 3? Звичайно, можна приєднувати по одному на основі нумерації, але це не завжди зручно. Тому перший доданок 15 заміняють сумою розрядних одиниць (1 десяток і 5 одиниць) і додають 3 до 5 одиниць:

15 + 3 == (10 + 5) + 3 = 10 + (5 + 3) = 10 + 8 = 18.

Ц і правила використовуються для розвитку уваги і кмітливості учнів при усних обчисленнях. Наприклад:



Тут найзручнішим є другий спосіб, бо число 7 дає в сумі з другим доданком 3 кругле число 10. 3'ясовують це на конкретних задачах і множинах. Наприклад: «На столі лежить в одній купці 9 зошитів у клітинку, а в другій — 3 зошити в лінійку. Учень поклав на стіл ще 7 зошитів. Скільки всього зошитів стало на столі?»

Вчитель підводить учнів до висновку, що тут найзручніше обчисли­ти, коли 7 зошитів покласти до 3 зошитів.

б) Додавання суми до суми.

Теоретичною основою додавання двоцифрових чисел є правило до­давання суми до, суми:

(а + b) + (с + d) = (а + с) + (b + d) = (а + d) + (b + с).

Для того щоб додати суму до суми, можна до одного з доданків пер­шої суми додати один із доданків другої, а до другого доданку першої суми — інший доданок другої суми і одержані результати додати.

Н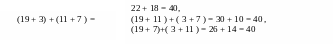 априклад:



Тут найзручнішим також буде другий спосіб. Покажемо, як можна з'ясувати це правило з учнями першого класу на конкретних задачах.

Задача. У першому класі 17 дівчаток і 19 хлопчиків, а в дру­гому — 13 дівчаток і 11 хлопчиків. Скільки учнів в обох класах? Розв'яжемо задачу двома способами:

1-й спосіб 2-й спосіб

Шукане число х всіх учнів скла- Шукане число х всіх учнів скла-дається з усіх учнів першого дається з усіх дівчаток першого і класу (17 + 19) і всіх учнів другого класів (17 + 13) і усіх другого класу (13+11), тобто хлопчиків обох класів (19 + 11),

х = (17 + 19) + (13 + 11), тобто х = (17 +13) + (19 + 11),

х = 36 + 24, х = 60. х = 30 + 30, х = 60.

Ці правила легко поширити на будь-яку кількість доданюв і об'єднати їх одним правилом: Якщо при додаванні маємо дужки, то їх мож­на, опустити і об'єднувати між собою доданки в будь-якій послідовності так, щоб обчислення виконувати найзручнішим способом.

Правило додавання суми до суми будь-якого числа доданків є теоретичною основою відомого із школи алгоритму додавання багатоцифрових чисел не тільки в десятковій системі числення, а і у будь-якій позиційній системі.