14. Интенсивность несклонности к риску, премия за риск (подход Марковица).

Если ЛПР не склонен к риску, график его функции полезности является выпукл вверх. В случае, если существ вторая произвольная от функции полезности, это равносильно тому, что <0. Однако непосредственно использовать для количественно оценки несклонности к риску нельзя. Шкала полезности является хоть и логической, но произвольной в том смысле, что линейное преобразование функции полезности, сохраняя упорядочение альтернатив, меняет значение функции и ее производных.

Необходимо, чтобы мера несклонности к риску обладала следующими условиями: 1.Показывала субъективное отношение к риску.

2. Была инвариантна относительно линейного преобразования функции полезности, т.е. оценок для функции u(x), v(x)=αu(x)+β, α>0.

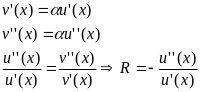В то же время отношение 1 и 2 произвольной не меняется при линейной трансформации и именно оно может быть использовано как количественная мера интенсивности несклонности к риску. Альтернативный подход состоит в том, что интенсивность несклонности к риску измеряется с помощью индивид-ой премии за риск. Пусть ЛПР обладает гарантированным доходом W₀ одновременно с простой лотереей . Свяжем с простой лотереей случайную величину выигрыша Х, ее математическое ожидание . Введем полезность одновременного обложения простой лотереи и гарантированного дохода . Вместе с Х эта полезность является случайной величиной и говорить о ее оптимизации можно в смысле ее математического ожидания: Если ЛПР не склонен к риску, он готов уступить участие в простой лотерее за денежную сумму, меньше, чем на некоторую величину _{которая} называется премией за риск. Величина премии за риск определяется из условия: .Абсолютное большинство функций полезности является монотонно возрастающими и потому имеют обратные. Берем функцию от обеих частей последнего равенства .

Сама формула называется формулой Марковица. Полученная фор-ла выраж премию за риск через субъект особ-ти ЛПР и хар-ки самой лотереи, заключается в величине Х.

15. Формула Эрроу-Пратта.

Величина премии за риск определяется из условия:

- безрисковый эквивалент одновременного обладания простой лотереей и гарантированным доходом. (формула Марковица). Величину премии за риск желательно разделить на составляющие, одна из которых выражает субъективные особенности ЛПР, а другая характеристики самой лотереи., заключ. в случ. величине Х. _.

Раскладываем обе части этого равенства по ф-ле Тейлора в окрестности точки :

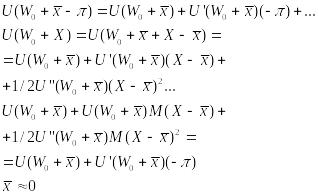
Где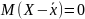 . ( ) = DX.

приравниваем _. Получаем:

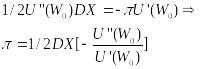. где DX – хар-ка L (лотереи); - коэффициент несклонности к риску.

- формула Эрроу-Пратта.

16. Понятие многошагового управляемого процесса. Формализация многошаговой детерминированной задачи принятия решения.

Процесс – это последовательная смена состояний, ход развития чего-то. Это развитие может происходить в дискретном или непрерывном времени. Процессы, протекающие в дискретном времени, то есть те, где изменения состояний происходит во вполне определенные моменты времени, называются многошаговыми или многоэтапными.

Процесс называется управляемым, если ЛПР имеет возможность влиять на его течение путем изменения некоторых параметров. При этом решение, принимаемое на каждом этапе, называется управлением.

Пусть некоторая физическая система S находится в начальном состоянии x1 из множества X1 и ее функционирование разбито на n этапов. Состояние системы на каждом этапе с номер j от 1 до n характеризуется параметром xj. Переход из состояния в состояние осуществляется посредством управления uj выбираемым на каждом этапе. В совокупности отдельные управления образуют вектор управлений или управленческую стратегию.

Понятие состояния описывает систему с позиций наличия некоторого ограниченного ресурса, регламентирующего выбор управления и обеспечивающего взаимную увязку отдельных этапов. Кроме того, состояние содержит в себе всю предысторию процессов, то есть должно быть описано с той степенью подробности, которая позволяет провести вычисления или оценку текущих альтернативных решений.

Определить текущее состояние можно, ответив на:

1. В чем проявляется связь между этапами?

2. Какая информация необходима для принятия управленческого решения на некотором этапе без проверки допустимости решений, принятых на предшествующих этапах.

С течением времени состояние системы меняется и она переходит в финальное состояние x _n+1 из соответствующего множества. Качество управленческого решения каждого этапа и, как следствие, всей управленческой стратегии, характеризуется функцией f(x1,u).

Задача состоит том, чтобы из всех возможных управленческих стратегий выбрать ту, что доставляет необходимый оптимум функции f

f(x1,u) стремится к min или max при u=(u1….)

Формализация многошаговой детерминированной задачи принятия решения.

Пусть некоторая физическая система S находится в начальном состоянии x₁ X₁ и процесс ее функционирования разбивается на n – этапов. На каждом этапе система переходит в очередное состояние под действием управления u_j U_j, выбираемого на этом этапе. Понятие состояния описывает систему с позиций наличия некоторого ограниченного ресурса, что обеспечивает взаимную увязку всех этапов.

Состояние системы заключает всю предысторию процесса в том смысле, что позволяет сформировать совокупность альтернативных управленческих решений и не содержит излишеств. Предполагается, что состояния системы определены на качественном уровне таким образом, что в каждый момент времени система может находиться ровно в одном состоянии. При определении состоянии системы следует ответить на 2 вопроса: 1) В чем проявляется связь м.у этапами 2) Какая информация необходима для принятия решения на этапе без проверки допустимости решений, принятых на пред-х этапах.