- •1. Парето-оптимальные решения многокритериальных задач и способы сужения границы Парето: субоптимизация, лексикографическая оптимизация, построение обобщенного критерия.
- •2. Метод анализа иерархий (метод Саати): определение значимости критериев, согласованность матрицы парных сравнений, определение весовых коэффициентов методом собственного вектора.
- •3. Критерии принятия решений в условиях неопределенности: методы Лапласа, Вальда, Сэвиджа, Гурвица.
- •4. Обобщенный критерий Гурвица для безопасной и опасной ситуаций.
- •Формализация ситуации риска, принципы доминирования.
- •6. Меры риска, масштабные и вероятностные.
- •7. Критерии принятия решений в условиях риска: ожидаемого значения (критерий Байеса), минимальной вариации, предельного уровня, наиболее вероятного исхода.
- •8. Критерий «ожидаемое значение – вариабельность результата», коэффициент склонности к риску, зоны склонности к риску.
- •9. Понятие кривой безразличия. Три типа кривых безразличия.
- •10. Понятие идеального эксперимента, обоснование его целесообразности.
- •11. Понятие неидеального эксперимента, алгоритм обоснования его целесообразности.
- •12. Смешанные стратегии как инструмент уменьшения риска.
- •13. Понятие функции полезности, алгоритм ее построения. Основные типы функций полезности.
- •14. Интенсивность несклонности к риску, премия за риск (подход Марковица).
- •15. Формула Эрроу-Пратта.
- •16. Понятие многошагового управляемого процесса. Формализация многошаговой детерминированной задачи принятия решения.
- •17. Характерные особенности многошаговых процессов принятия решений. Принцип оптимальности Беллмана.
- •18. Марковские процессы с дискретными состояниями. Формула Колмогорова-Чепмена.
- •19. Марковские процессы принятия решений с конечным числом этапов: метод итераций по стратегиям и его возможные обобщения.
- •20.Марковские процессы принятия решений с бесконечным числом этапов: специфика постановки задачи. Отыскание оптимальных стратегий на бесконечном временном горизонте методом полного перебора.
- •21. Метод итераций по стратегиям без дисконтирования (для бесконечного числа этапов).
- •22. Случайные процессы с непрерывным временем, их формализация. Система дифференциальных уравнений Колмогорова, правила ее составления.
- •23. Потоки событий, их свойства. Простейший (пуассоновский стационарный) поток.
- •24. Вероятностные характеристики простейшего потока.
- •25. Роль экспоненциального распределения в исследовании простейших потоков. Финальные состояния системы, в которой протекает марковский процесс.
- •26. Процессы гибели и размножения, финальные вероятности состояний.
- •27. Процессы гибели и размножения в системе с m узлами, финальные вероятности состояний.
- •28. Системы массового обслуживания, их основные компоненты и характеристики функционирования.
- •29. Многоканальные системы массового обслуживания с отказами.
- •30. Одноканальные системы массового обслуживания с ожиданием и ограничением на длину очереди.
13. Понятие функции полезности, алгоритм ее построения. Основные типы функций полезности.
Функция полезности — функция, показывающая убывание предельной полезности блага с ростом его количества
Алгоритм построения функции полезности:
1.из некоторых соображений ограничиваем интервал рассматриваемых денежных сумм, приняв в качестве этого интервала [s, S] ([-20; 40]);
2.вводим произвольную, но логическую шкалу полезности (логич в том смысле, что большим ден суммам отвеч большее значение полезности): U(s) = 0 ; U(S) = 100 (ед. полез-ти).
3.для
каждого значения
![]() рассчитывают
нейтральную вероятность p0
такую, что обладание денежной суммой в
x
ед. равносильно участию в лотерее, где
вероятность выиграть S
равна p0,
а s
руб. – (1 – p0).
рассчитывают
нейтральную вероятность p0
такую, что обладание денежной суммой в
x
ед. равносильно участию в лотерее, где
вероятность выиграть S
равна p0,
а s
руб. – (1 – p0).
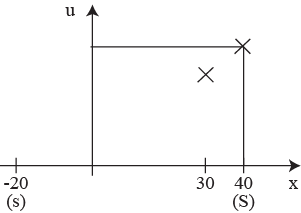
0,9 – много; 0,8 – мало; 0,85 – мало; p0 = 0,875 – хватит.
![]() ;
x0,5
– середина
;
x0,5
– середина
Виды отношений к риску. Простой лотереей называется лотерея с двумя исходами L{x1, x2; p}, x1 > x2. p – вероятность получить выигрыш x1. (1 – p) – вероятность получить выигрыш x2.
Ожидаемый
выигрыш в простой лотерее:
![]() .
Опр. Гарантированным эквивалентом
простой лотереи наз ден сумма В, обладание
которой для ЛПР равносильно участию в
лотерее. Из сопоставления ожидаемого
выигрыша
.
Опр. Гарантированным эквивалентом
простой лотереи наз ден сумма В, обладание
которой для ЛПР равносильно участию в
лотерее. Из сопоставления ожидаемого
выигрыша
![]() и гарантированного
эквивалента В выявляется склонность
ЛПР к риску: 1.если ожидаемый выигрыш
и гарантированного
эквивалента В выявляется склонность
ЛПР к риску: 1.если ожидаемый выигрыш
![]() ,
значит ЛПР склонен к риску; 2.если
ожидаемый выигрыш
,
значит ЛПР склонен к риску; 2.если
ожидаемый выигрыш
![]() ,
значит ЛПР не склонен к риску; 3.если
ожидаемый выигрыш
,
значит ЛПР не склонен к риску; 3.если
ожидаемый выигрыш
![]() ,
значит ЛПР нейтрален к риску.
,
значит ЛПР нейтрален к риску.
Введем полезность простой лотереи аналогично тому, как это делалось в алгоритме построения функции полезности:
![]()
Имея в виду, что шкала полез-ти явл произв-ой, но логич (большим ден. суммам отвеч больш. Знач полез-ти), применим функ-ию полез-ти к соотн 1-3:
1.![]() .
График функции
полезности является выпуклым вниз
.
График функции
полезности является выпуклым вниз
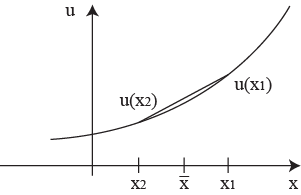
2.![]() .
ЛПР не склонен к риску
.
ЛПР не склонен к риску
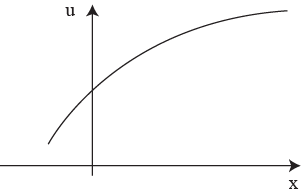
3.![]() .
ЛПР нейтрален к риску
.
ЛПР нейтрален к риску
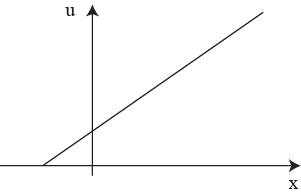
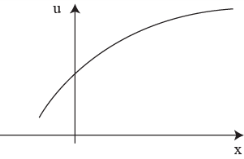
1.ЛПР склонен к риску |
2.ЛПР не склонен к
риску |
3.ЛПР нейтрален к риску
|
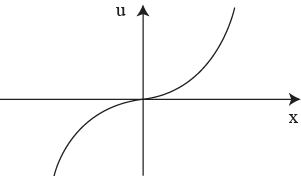
4.“Экстремист”
– боится долговых обязательств |
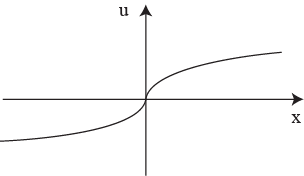
5.“Зануда” – индифферентен, ему все равно
7.Обладание малым очень радует, чем больше долг, тем мрачнее
|
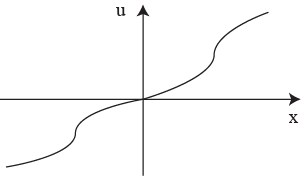
6.Типичный человек:
сначала рискует, после достижения
определенной суммы не рискует, но
готов рискнуть малой суммой
|
|
8.Настроение человека, у которого есть долг (имеет долг в а руб.)
|
Применение функции полезности в страховании:
Пусть
финансовое состояние ЛПР оценивается
W.
Предполагается, что можно оценить
вероятность р, с которой ЛПР теряет
часть своего богатства в размере L.
ЛПР может купить страховой полис, в
соответствии с которым, ему возмещается
ущерб в размере q.
Плата за страхование составляет
![]() ,
где
,
где
![]() -
доля страховки в объеме нанесенного
ущерба. Определить оптимальное страховое
возмещение q*,
при которой ожидаемая полезность ЛПР
будет наибольшей.
-
доля страховки в объеме нанесенного
ущерба. Определить оптимальное страховое
возмещение q*,
при которой ожидаемая полезность ЛПР
будет наибольшей.
![]() -
наступление страхового случая.
-
наступление страхового случая.
![]() -
не наступление страхового случая
-
не наступление страхового случая
![]()
При
не наступлении (1-р)=
.
Средний
ожидаемый доход:
![]()
В условиях конкуренции страховая компания получает выгоды за счет взносов.
![]()
В предп-ии, что ф-ия полез-ти явл строго монотонной, а ее график – строго выпукл вверх, первая произв-я функции полез-ти также облад св-ом монот-ти, и потому из рав-ва произ-ых можно сделать вывод о рав-ве их аргум-ов.
Последнее
означает, что из равенства производных
следует равенство их аргументов.
![]()