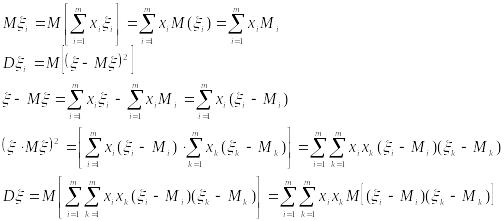10. Понятие идеального эксперимента, обоснование его целесообразности.

Понятие "идеальный эксперимент" ввел в употребление Г. Кэмпбелл. Идеальный эксперимент – эксперимент, предполагающий варьирование экспериментатором только независимой переменной и контроль зависимой переменной. Другие условия эксперимента остаются неизменными. Идеальный эксперимент предполагает эквивалентность испытуемых, неизменность их характеристик во времени, отсутствие самого физического времени (как это ни парадоксально звучит), возможность проводить эксперимент бесконечно. Следствием этого является проведение всех экспериментальных воздействий одновременно.

Идеальный эксперимент противостоит реальному эксперименту.

Реальный эксперимент – эксперимент, в котором изменяются не только интересующие исследователя переменные, но и ряд других условий. Соответствие идеального эксперимента реальному выражается в такой его характеристике, как внутренняя валидность (validity).

Внутренняя валидность – характеристика эксперимента, показывающая, насколько идеальный эксперимент соответствует реальному, а также указывающая на достоверность результатов, которую обеспечивает реальный эксперимент по сравнению с идеальным. Внутренняя валидность характеризует меру влияния на зависимую переменную тех условий (независимой переменной), которые варьирует экспериментатор.

Чем больше влияние на зависимую переменную не контролируемых исследователем условий, тем ниже внутренняя валидность эксперимента. Следовательно, больше вероятность того, что факты, обнаруженные посредством эксперимента, являются артефактами.

С точки зрения Кемпбелла, хороший эксперимент должен:

1) выявлять временную последовательность предполагаемых причины и следствия;

2) показывать, что вероятные причины и эффект взаимосвязаны (ковариантны);

3) исключать влияние побочных переменных, которыми можно было бы объяснить экспериментальный эффект;

4) исключать альтернативные гипотезы о теоретических конструктах, объясняющих эту связь.

11. Понятие неидеального эксперимента, алгоритм обоснования его целесообразности.

12. Смешанные стратегии как инструмент уменьшения риска.

Пусть ЛПР имеет m чистых стратегий A_i. Природа м/нах-ся в одном из n состояний Ѳ_j с вер-ю p_j
Для каждой игровой сит-ии (A_i, Ѳ_j) известен выигрыш ЛПР a_ij.		a_ij – выигрыш
В ситуации риска выбор ЛПР своей i-той чистой стратегии приводит к реализации случ. величины:
, ,
Предположим, что ЛПР воспользуется своей смешанной стратегией:
Это приводит к реализ-ии с.в. ξ вида:
Получим числовые хар-ки с.в.
Показатель коввариации с.в. и
Дисперсия с.в. предст. собой квадратичную форму, переменными которой явл-ся компоненты смеш. стратегии, а коэфф-ми – пок-ли ковариации.
Коэффициент корреляции
Суть эффекта диверсификации сводится к сл. моментам:
1	Применение смеш. страт-ии никогда не увеличит возможный выигрыш ЛПР. Смеш. страт-ии исп-я исключительно для снижения риска. Возм-ть этого сниж. опр-я зависимостью м/у с.в. и
2	Применение смешанных стратегий может уменьшить риск ЛПР, но величина этого уменьшения самым существенным образом зависит от формы связи между случайными величинами.		, равномерн. страт-ия - . Т.е. увеличение числа смешиваемых стратегий позволяет снизить риск ЛПР практически до 0.
3	Между случайными величинами ξ_i и ξ_k существует полная прямая корреляция, т.е.:
4	Полная обратная корреляция, т.е.: Рассмотрим для случая m= 2: Принят. смеш-ой страт-ии вполне исключ. риск. Дост-но исп-ть смеш. страт-ию, комп-ты кот-й обратно проп-ны пок-ям риска случ. величин и
5	В общем случае, когда м/у с.в. и имеется корреляция, но она не явл-ся полной, величина пок-ля риска, возникшего при применении смеш. стратегии, нах-ся по общей формуле, прим-е кот-й предполагает известные пок-ли ковариации или коэф-ты корреляции с.в. При этом возникает вопрос, при какой стратегии ЛПР его риск минимален? Матем. формулировка и решение этой задачи принцип. сложности не представл., поскольку пок-ль риска (дисперсия или ст. отклонение) представл. собой непрерывн. ф-ию, опред-ую на огранич-е замкнутом множ-ве смеш-х стратегий. По т. Вейерштрасса, непрерыв. функ-ия на замкнутом огр. множ-ве всегда достигает наиб. и наим. значения.