7. Критерии принятия решений в условиях риска: ожидаемого значения (критерий Байеса), минимальной вариации, предельного уровня, наиболее вероятного исхода.

Критерий ожидаемого значения. Каждая стратегия ЛПР оценивается по среднему ожидаемому значению: A_i: . Если А – матрица выигрышей, то стратегия находится из условия максимизации: . Если А – матрица проигрышей, то стратегия находится из условия минимизации: .

Критерий минимальной вариации. Каждая альтернатива A_i оценивается присущим ей риском, измеренным стандартным отклонением σ_i или коэффициентом вариации V_i. Оптимальной считается та альтернатива, для которой эта оценка является наименьшей. ; .

Критерий предельного уровня. Исходя из некоторых соображений, устанавливается предельное значение случайной величины, характеризующее качество решения. Любая альтернатива, превышающая установленный порог, считается оптимальной. Критерий предельного уровня не дает единственного оптимального решения. Скорее он соответствует приемлемому способу действия – это недостаток. Достоинство: применение критерия не требует точной информации о законе распределения случайной величины. При назначенном предельном уровне достаточно приближенной информации о ситуации принятия решения.

4.Критерий наиболее вероятного исхода. Каждая случайная величина, описывающая исход применения той или иной стратегии, заменяется детерминированной величиной. За эту величину принимается то значение случайной величины, которое достигается с наибольшей вероятностью: A_i:

ai1	ai2	…	ain
p1	p2	…	pn

.

(a_i с волной)

Главный недостаток: этот критерий нельзя применять в том случае, когда закон распределения случайной величины не имеет четко выраженного максимума.

8. Критерий «ожидаемое значение – вариабельность результата», коэффициент склонности к риску, зоны склонности к риску.

Пусть критерий X показывает выигрыш ЛПР. Оптимальной стратегией ЛПР считается та, которая доставляет максимум функции: _. λ – числовой параметр, характеризующий несклонность ЛПР к риску. Оценить приемлемый для ЛПР уровень λ можно с помощью неравенства Чебышева:

(вероятность отклонения от математического ожидания больше, чем на а).

_{Применяя обобщенный критерий, ЛПР оценивает каждую свою стратегию числом: .} Ситуация риска, т.е. то, что истинное значение случайной величины X окажется меньше расчетной оценки значит, что: (подводим под неравенство Чебышева); . Если λ =3 => p = 90%. Если количественный показатель X представляет собой проигрыш ЛПР, то оптимальной считается та стратегия, которая доставляет минимум функции:

9. Понятие кривой безразличия. Три типа кривых безразличия.

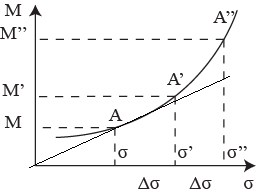
Кривой безразличия называется линия на корд. плоскости 0σМ, где σ – риск, измеренный стандартным отклонением, М - мат.ожидание результата., все точки которой ЛПР воспринимает как равноденные для себя.

, всегда одного знака, поскольку лучший результат сопряжен с большими рисками. > 0. - локальный коэффициент замещения (ЛКЗ). . Если принять за ед. изм. риска, то , т.е. ЛКЗ показывает, приращение результата, которое компенсирует изменение риска на единицу. Геометрический смысл ЛКЗ – угловой коэффициент секущей (tg угла наклона этой кривой). Именно динамика ЛКЗ позволяет оценить изменение отношения ЛПР к риску. Типы кривой безразличия

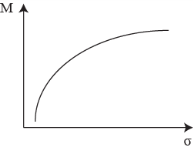
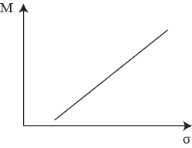
Возрастающая КБ (несклонность к риску)	Убывающая КБ	Постоянная КБ

Для возр. I. графически возрастает; I. выпуклая вниз. Общий вывод: если точки, изображающие альтернативы, не лежат на одной кривой безразличия, то оптимальной является та из них, которая расположена на более высокой кривой.

Картой безразличия называется область на числовой плоскости 0σM, через каждую точку которой проведена кривая безразличия. Имея карту безразличия, можно обосновать целесообразность выбора одной из двух рисковых альтернатив.

Пусть имеются 2 альтернативы с оценками A₁(σ₁, M₁) и A₂(σ₂, M₂). Относительно взаимного расположения изображенных этими альтернативами точек возможно 3 предположения: 1.они лежат на одной кривой безразличия – альтернативы равнозначные, можно выбирать любую; 2.они не лежат на одной кривой, но альтернатива A₂ попадает в область, доминируемую А₁. Тогда выбираем А₁; 3.они не лежат на одной кривой, альтернатива A₂ не попадает в область, доминируемую А₁:

Общий вывод: если точки, изображающие альтернативы, не лежат на одной кривой безразличия, то оптимальной является та из них, которая расположена на более высокой кривой.