Формализация ситуации риска, принципы доминирования.

Закон распределения содержит исчерпывающую информацию о случайной величине. Однако для принятия управленческих решений требуются обобщающие характеристики этой величины. Ими являются:

1.математическое ожидание (это не мера риска, а ожидаемый результат): . 2.дисперсия – возможное отклонение случайной величины от ожидаемого значения: DX = M[X – MX]²_. Для случайной величины дискретного типа:

. На практике используется следующая формула (можно использовать в качестве меры риска): DX = M(X²) – (MX)².

3.стандартное (среднеквадратичное отклонение) – разброс случайной величины относительно ее ожидаемого значения: _. Пусть x – прибыль ЛПР. Коэффициент риска данной альтернативы – это вероятность, что истинное значение меньше расчетного.

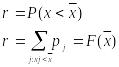
4.полудисперсия. (semi – полудисперсия).

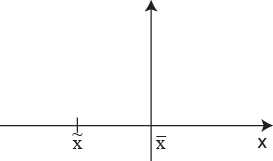
(x с волной)

5.относительная мера риска – коэффициент вариации – сопоставление отклонения с ожидаемым результатом: . По значению VX рисковые альтернативы делятся на 3 группы: 1.VX < 0,1 – малый риск; 2.0,1 <=VX <= 0,25 – средний риск; 3.VX > 0,25 – высокий риск

Принципы доминирования в принятии рискованных решений.

Пусть имеется 2 альтернативы A и B, каждая из кот хар-ся своим рядом распределения: A(x_j, p_j­), B(y_j, p_j). 1.Абсолютное доминирование: Альтернатива A абсолютно доминирует альтернативу B, если выполняется неравенство: . Т.е. в том случае, когда мин выигрыш для альт A не меньше макс выигрыша для альт B. 2.Доминирование по состоянию: Альтернатива A доминирует альтернативу B, если для всех номеров j выполняется: .и хотя бы однажды: _. 3.Доминирование по вероятности: Альтернатива A доминирует по вероятности альтернативу B, если для любого возможногёо значения выигрыша а вероятность получить выигрыш меньший, чем а, для альтернативы А меньше соответствующей вероятности для альтернативы B, т.е.: . и хотя бы для одного значения a имеет место строгое неравенство.

Прибыль xjyj	FA( )	FB( )	FA - FB
упорядочим значения по возрастанию

F_A ( ) – функция распределения в соответствующей точке для проекта А. Если числа одного знака, то есть доминирование по вероятности, иначе – нет.

6. Меры риска, масштабные и вероятностные.

+ начало 5 вопроса

Мера риска – это абсолютная (относительная) величина или вероятностный показатель возможных отклонений результатов хозяйственной деятельности в заданных условиях в течение определенного времени. Абсолютная величина результатов выражается в денежной форме и характеризует их среднее значение или разброс относительно среднего значения. Относительная величина выражается в дольном или процентном отношении к ожидаемым результатам. В качестве вероятностной меры риска обычно используют закон распределения случайной величины, устанавливающий связь между ее возможными значениями и вероятностями их реализации. Рассматривая риск с точки зрения его оценки, необходимо решить следующую задачу:

1.выделить и формализованно описать все возможные варианты окружающей обстановки (состояния природы);

2. рассчитать или оценить вероятности реализации этих вариантов;

3.количественно оценить каждую ситуацию принятия решения, которая на содержательном уровне понимается как пара, составленная из стратегии ЛПР и состояния окружающей среды.

Вероятности реализации отдельных вариантов обстановки рассчитываются количественными методами, либо оцениваются на качественном уровне. Количественные методы делятся на 3 группы: 1.прямые вероятностные методы m/n (количество случайных наблюдений / общее число); 2.приближенные методы (возвращение кредита); 3.косвенный (метод аналогий).

Информация, получаемая при решении перечисленных задач, обобщенно представляется законом распределения случайной величины, который для случайной величины дискретного типа представляет собой ряд распределения:

Возможные значения случайной величины xj	x1	x2	…	xn	x1<x2<…<xn
Вероятности их реализации pj	p1	p2	…	pn
Кумулятивная функция (распределения)	F(x1)	F(x2)	…	F(xn)	F(x) = 0, x <= x1 F(x) = 1, x > xn

F_x(x) = P(X < x). Для случайной величины дискретного типа: функция распределения .