
- •1. Парето-оптимальные решения многокритериальных задач и способы сужения границы Парето: субоптимизация, лексикографическая оптимизация, построение обобщенного критерия.
- •2. Метод анализа иерархий (метод Саати): определение значимости критериев, согласованность матрицы парных сравнений, определение весовых коэффициентов методом собственного вектора.
- •3. Критерии принятия решений в условиях неопределенности: методы Лапласа, Вальда, Сэвиджа, Гурвица.
- •4. Обобщенный критерий Гурвица для безопасной и опасной ситуаций.
- •Формализация ситуации риска, принципы доминирования.
- •6. Меры риска, масштабные и вероятностные.
- •7. Критерии принятия решений в условиях риска: ожидаемого значения (критерий Байеса), минимальной вариации, предельного уровня, наиболее вероятного исхода.
- •8. Критерий «ожидаемое значение – вариабельность результата», коэффициент склонности к риску, зоны склонности к риску.
- •9. Понятие кривой безразличия. Три типа кривых безразличия.
- •10. Понятие идеального эксперимента, обоснование его целесообразности.
- •11. Понятие неидеального эксперимента, алгоритм обоснования его целесообразности.
- •12. Смешанные стратегии как инструмент уменьшения риска.
- •13. Понятие функции полезности, алгоритм ее построения. Основные типы функций полезности.
- •14. Интенсивность несклонности к риску, премия за риск (подход Марковица).
- •15. Формула Эрроу-Пратта.
- •16. Понятие многошагового управляемого процесса. Формализация многошаговой детерминированной задачи принятия решения.
- •17. Характерные особенности многошаговых процессов принятия решений. Принцип оптимальности Беллмана.
- •18. Марковские процессы с дискретными состояниями. Формула Колмогорова-Чепмена.
- •19. Марковские процессы принятия решений с конечным числом этапов: метод итераций по стратегиям и его возможные обобщения.
- •20.Марковские процессы принятия решений с бесконечным числом этапов: специфика постановки задачи. Отыскание оптимальных стратегий на бесконечном временном горизонте методом полного перебора.
- •21. Метод итераций по стратегиям без дисконтирования (для бесконечного числа этапов).
- •22. Случайные процессы с непрерывным временем, их формализация. Система дифференциальных уравнений Колмогорова, правила ее составления.
- •23. Потоки событий, их свойства. Простейший (пуассоновский стационарный) поток.
- •24. Вероятностные характеристики простейшего потока.
- •25. Роль экспоненциального распределения в исследовании простейших потоков. Финальные состояния системы, в которой протекает марковский процесс.
- •26. Процессы гибели и размножения, финальные вероятности состояний.
- •27. Процессы гибели и размножения в системе с m узлами, финальные вероятности состояний.
- •28. Системы массового обслуживания, их основные компоненты и характеристики функционирования.
- •29. Многоканальные системы массового обслуживания с отказами.
- •30. Одноканальные системы массового обслуживания с ожиданием и ограничением на длину очереди.
3. Критерии принятия решений в условиях неопределенности: методы Лапласа, Вальда, Сэвиджа, Гурвица.
1.Критерии
Лапласа (недостаточного обоснования).
Все состояния
природы считаются равновероятными, и
каждое из них реализуется с вероятностью
1/n. Каждая стратегия ЛПР Ai
оценивается средней величиной:
![]() .
Если матрица А –
матрица выигрышей, то оптимальная
стратегия, доставляющая максимум
.
Если матрица А –
матрица выигрышей, то оптимальная
стратегия, доставляющая максимум
![]() ,
проигрыш – минимум
,
проигрыш – минимум
2.Критерий
Вальда (пессимистический, по наихудшему
варианту): Оценивает
каждую стратегию ЛПР по наихудшему
варианту развития событий.
А – матрица
выигрышей
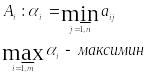 ;
А – матрица проигрышей
;
А – матрица проигрышей
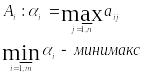 .
.
3.Критерий
Сэвиджа. Применение
этого критерия требует предварительного
построения матрицы рисков Rij
= (rij).
А – матрица
выигрышей
![]() -
максимальный элемент j
– столбца
-
максимальный элемент j
– столбца
![]() .
А – матрица
проигрышей
.
А – матрица
проигрышей
![]() -
минимальный элемент j
– столбца
-
минимальный элемент j
– столбца
![]() .
Другое название – матрица сожалений
(об упущенной выгоде). В независимости
от того, какой была исходная матрица
(выигрыша/проигрыша), матрица риска
всегда является матрицей потерь
(проигрыша). Решение по матрице рисков
находится в силу минимаксного варианта
критерия Вальда: каждая стратегия ЛПР
оценивается максимальным риском, ей
присущим, а затем этот максимальный
риск минимизируется.
.
Другое название – матрица сожалений
(об упущенной выгоде). В независимости
от того, какой была исходная матрица
(выигрыша/проигрыша), матрица риска
всегда является матрицей потерь
(проигрыша). Решение по матрице рисков
находится в силу минимаксного варианта
критерия Вальда: каждая стратегия ЛПР
оценивается максимальным риском, ей
присущим, а затем этот максимальный
риск минимизируется.
4.
Критерий Гурвица.
![]() -
показатель
оптимизма ЛПР. Каждая стратегия
оценивается числом Gi(λ),
построение которого зависит от типа
матрицы:
-
показатель
оптимизма ЛПР. Каждая стратегия
оценивается числом Gi(λ),
построение которого зависит от типа
матрицы:
А – матрица
выигрышей
![]() .
Обобщенная оценка
стратегии
.
Обобщенная оценка
стратегии
![]() .
.
А
– матрица проигрышей
![]() .
Обобщенная оценка
стратегии
.
Обобщенная оценка
стратегии
![]()
4. Обобщенный критерий Гурвица для безопасной и опасной ситуаций.
Пусть
игра с природой задается матрицей
выигрышей Amxn
= (aij).
Переупорядочим элементы строки матрицы
А. расположив их по не убыванию:
![]() .
В результате
получаем матрицу Bmxn
= (bij).
Пусть имеется
.
В результате
получаем матрицу Bmxn
= (bij).
Пусть имеется
![]() .
Интерпретируем их как веса, присваиваемые
отдельным выигрышам ЛПР. Число
.
Интерпретируем их как веса, присваиваемые
отдельным выигрышам ЛПР. Число
![]() называется
обобщенным показателем эффективности
i-той стратегии ЛПР, из условия максимизации
которого и выбирается обобщенная
стратегия. Введем обозначения:
называется
обобщенным показателем эффективности
i-той стратегии ЛПР, из условия максимизации
которого и выбирается обобщенная
стратегия. Введем обозначения:
![]()
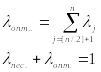 .
Если ЛПР оценивает
ситуацию принятия решения как опасную,
то коэффициент пессимизма λпес.
> λопт.;
в безопасной ситуации – наоборот. Если
ЛПР оценивает ситуацию принятия решения
как опасную, то требуемое соотношение
показателей оптимизма и пессимизма
можно обеспечить, подчинив весовые
коэффициенты λj
принципу невозрастания средних выигрышей,
т.е. вычислив их из пропорции:
.
Если ЛПР оценивает
ситуацию принятия решения как опасную,
то коэффициент пессимизма λпес.
> λопт.;
в безопасной ситуации – наоборот. Если
ЛПР оценивает ситуацию принятия решения
как опасную, то требуемое соотношение
показателей оптимизма и пессимизма
можно обеспечить, подчинив весовые
коэффициенты λj
принципу невозрастания средних выигрышей,
т.е. вычислив их из пропорции:
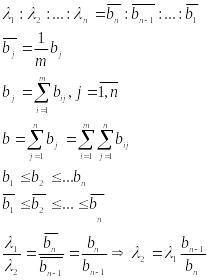 .
Формальной заменой
фиксированного индекса 2 на произвольный
индекс j
получаем:
.
Формальной заменой
фиксированного индекса 2 на произвольный
индекс j
получаем:
![]() .
Найденное выражение
λj
подставляем в нормировочное равенство:
.
Найденное выражение
λj
подставляем в нормировочное равенство:
 .
.
![]() .
Если ЛПР оценивает
ситуацию принятия решений как безопасную,
то весовые коэффициенты λj
можно найти по принципу неубывания
средних выигрышей по пропорции:
.
Если ЛПР оценивает
ситуацию принятия решений как безопасную,
то весовые коэффициенты λj
можно найти по принципу неубывания
средних выигрышей по пропорции:
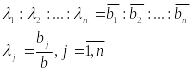 .
Указанный подход
можно применить и к классическому
варианту критерия Гурвица, определив
критерии оптимизма и пессимизма в
зависимости от оценки ситуации: опасная
.
Указанный подход
можно применить и к классическому
варианту критерия Гурвица, определив
критерии оптимизма и пессимизма в
зависимости от оценки ситуации: опасная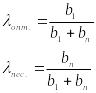 ;
безопасная
;
безопасная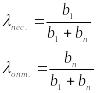 .
Выводы: 1.при принятии
решений в условиях неопределенности
достаточно ограничиться лишь первоначально
имеющимися, т.е. чистыми стратегиями
ЛПР при условии, что задача предполагает
выбор одного наилучшего способа действия
из имеющихся альтернатив;
.
Выводы: 1.при принятии
решений в условиях неопределенности
достаточно ограничиться лишь первоначально
имеющимися, т.е. чистыми стратегиями
ЛПР при условии, что задача предполагает
выбор одного наилучшего способа действия
из имеющихся альтернатив;
2.если условиями задачи допускается физическое смешение чистых стратегий ЛПР, то пропорции этого смешения можно рассчитать как компоненты оптимальной смешанной стратегии в антагонистическом конфликте с природой;
3.переход к смешанным стратегиям никогда не сможет увеличить выигрыш ЛПР, а может лишь сократить его возможный риск, где риск понимается в смысле Сэвиджа как недополученная прибыль.
5. Понятие ситуации риска, основные постулаты риск-менеджмента, формализация ситуации риска, принципы доминирования.
Риск – это возможность ненаступления некоторых ожидаемых событий и возможность отклонения каких-либо величин от их ожидаемых расчетных значений. Экономический риск представляет собой неоднозначность экономических результатов хозяйствующего субъекта в будущем, обусловленную неоднозначностью самого этого будущего.
1.Не бывает риска без деятельности и не бывает деятельности, свободной от риска. Относительно экономического риска можно утверждать, что даже отказ ЛПР от рискованных действий влечет за собой риск, в частности, риск упущенной выгоды при благоприятном развитии ситуации.
2.Риск всегда связан с ожиданиями, оценками и решениями субъекта и не существует безотносительно его. Применительно к экономическому риску это означает, что категория риска имеет смысл только относительно ЛПР и только относительно доступных ему вариантов решений. 3.Риск отражает решения, с помощью которых связывается время, т.е. хотя будущее не может быть известно в полной степени, даже то будущее, которое создается решениями ЛПР.
4.Необходимо различать риск и его меру.
Пусть качество управленческого решения количественно оценивается одним числовым показателем, характеризующим выгоды или потери ЛПР. В условиях риска этот показатель становится случайной величиной и для его измерения наиболее пригодна вероятностная схема.
