2. Метод анализа иерархий (метод Саати): определение значимости критериев, согласованность матрицы парных сравнений, определение весовых коэффициентов методом собственного вектора.

Метод предназначен для ранжирования (упорядочения) объектов в применении к следующей задаче: имеется конечное множество объектов {p₁, p₂, …, p_m}, требуется ранжировать их, приписав каждому из объектов весовой коэффициент, который в совокупности образует вектор весовых коэффициентов или вектор приоритетов.

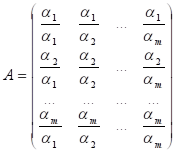
Предположим, что весовые коэффициенты известны, составим из них матрицу отношений A=(a_ij­).

Матрица А обладает тем свойством, что вектор приоритетов является собственным вектором этой матрицы отвечающей собственному числу (λ).

Еe собственным вектором называется нетривиальный вектор x удовлетворяющий матричному уравнению AX=λX.

На практике вектор приоритетов находится построением и анализом матрицы парных сравнений, которая в определенной степени заменяет матрицу отношений (А).

Шкала превосходства

Количественная оценка	Содержательное описание степени превосходства
1	Равная важность
3	Умеренное превосходство
5	Существенное превосходство
7	Значительное превосходство
9	Подавляющее превосходство
2, 4, 6, 8	Промежуточные значения между соседними оценками
Обратные величины

По своему построению матрица парных сравнений является положительной и обратно симметричной. Для того, чтобы матрица парных сравнений выражала непротиворечивые суждения ЛПР она должна дополнительно удовлетворять условию согласованности.

Формальным обоснованием требования согласованности является следующее утверждение: если матрица А является согласованной, то существуют положительные числа альфа, что a_ij=α_i/α_j.

Матрица парных сравнений, отражающая субъективное мнение ЛПР, может быть несогласованной. Важно лишь, чтобы степень несогласованности не превышала какой-то предельный уровень.

Измерение степени согласованности базируется на двух фактах из линейной алгебры.

1.Если в положительной матрице А выполняется а_ii = 1, то . Из этого следует, что в идеально согласованной матрице , остальные собственные числа = 0.

2.Собственный числа являются непрерывными функциями от элементов матрицы.

Из этих утверждений следует что если матрица парных сравнений мало отличается от идеально согласованной матрицы отношений, то λ_max матрицы парных сравнений мало отличается от m. Для количественной оценки возможных отклонений вводится коэффициент согласованности

RI - стохастический индекс согласованности

CI – это индекс согласованности

CR<=0,1 – согласованность считается приемлемой, в противном случае нет.

Собственное число и собственный вектор матрицы А находятся приближенно. Для этого на ряду с матрицей парных сравнений А рассматривается нормализованная матрица N того же порядка, состоящая из чисел n_ij, полученные делением кажд эл-та столбца на сумму эл-тов кажд столбца.

Если все столбцы матрицы N одинаковы, значит матрица А является идеально согласованной и любой столбец матрицы N может быть выбран в качестве вектора приоритета. В противном случае элементы матрицы А усредняются по строкам, т.е. сумма элементов в каждой строке делится на число элементов в этой строке и это число принимается за приоритет этого объекта _. В совокупности и образуют вектор приоритета.

Для проверки непротиворечивости полученного результата необходимо найти λ_max и проверить согласованность. По определению λ_max находится из решения матричного уравнения, которое равносильно линейной система, где i-е уравнение имеет вид:

(по определению)

Просуммируем эти уравнения.

(сумма равна 1)

Для того чтобы найти λ_max достаточно матрицу парных сравнений А умножить на приближенный вектор приоритетов и получившиеся произведения сложить (в формуле ниже – вектор).