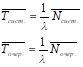- •1. Парето-оптимальные решения многокритериальных задач и способы сужения границы Парето: субоптимизация, лексикографическая оптимизация, построение обобщенного критерия.
- •2. Метод анализа иерархий (метод Саати): определение значимости критериев, согласованность матрицы парных сравнений, определение весовых коэффициентов методом собственного вектора.
- •3. Критерии принятия решений в условиях неопределенности: методы Лапласа, Вальда, Сэвиджа, Гурвица.
- •4. Обобщенный критерий Гурвица для безопасной и опасной ситуаций.
- •Формализация ситуации риска, принципы доминирования.
- •6. Меры риска, масштабные и вероятностные.
- •7. Критерии принятия решений в условиях риска: ожидаемого значения (критерий Байеса), минимальной вариации, предельного уровня, наиболее вероятного исхода.
- •8. Критерий «ожидаемое значение – вариабельность результата», коэффициент склонности к риску, зоны склонности к риску.
- •9. Понятие кривой безразличия. Три типа кривых безразличия.
- •10. Понятие идеального эксперимента, обоснование его целесообразности.
- •11. Понятие неидеального эксперимента, алгоритм обоснования его целесообразности.
- •12. Смешанные стратегии как инструмент уменьшения риска.
- •13. Понятие функции полезности, алгоритм ее построения. Основные типы функций полезности.
- •14. Интенсивность несклонности к риску, премия за риск (подход Марковица).
- •15. Формула Эрроу-Пратта.
- •16. Понятие многошагового управляемого процесса. Формализация многошаговой детерминированной задачи принятия решения.
- •17. Характерные особенности многошаговых процессов принятия решений. Принцип оптимальности Беллмана.
- •18. Марковские процессы с дискретными состояниями. Формула Колмогорова-Чепмена.
- •19. Марковские процессы принятия решений с конечным числом этапов: метод итераций по стратегиям и его возможные обобщения.
- •20.Марковские процессы принятия решений с бесконечным числом этапов: специфика постановки задачи. Отыскание оптимальных стратегий на бесконечном временном горизонте методом полного перебора.
- •21. Метод итераций по стратегиям без дисконтирования (для бесконечного числа этапов).
- •22. Случайные процессы с непрерывным временем, их формализация. Система дифференциальных уравнений Колмогорова, правила ее составления.
- •23. Потоки событий, их свойства. Простейший (пуассоновский стационарный) поток.
- •24. Вероятностные характеристики простейшего потока.
- •25. Роль экспоненциального распределения в исследовании простейших потоков. Финальные состояния системы, в которой протекает марковский процесс.
- •26. Процессы гибели и размножения, финальные вероятности состояний.
- •27. Процессы гибели и размножения в системе с m узлами, финальные вероятности состояний.
- •28. Системы массового обслуживания, их основные компоненты и характеристики функционирования.
- •29. Многоканальные системы массового обслуживания с отказами.
- •30. Одноканальные системы массового обслуживания с ожиданием и ограничением на длину очереди.
29. Многоканальные системы массового обслуживания с отказами.
Задача Эрланга
Имеется
m
каналов на которые поступает простейший
поток интенсивности λ. Поток обслуживания
каждым каналом имеет интенсивность
 .
Определить показатели функционирования
системы и кач-ва обслуживания.
.
Определить показатели функционирования
системы и кач-ва обслуживания.
Будем нумеровать состояние системы по кол-ву заявок в ней нах-ся:
x0 – 0 каналов занято, m свободно, x1 – 1 канал занят, (m-1) свободно, xm – m каналов занято, 0 свободно
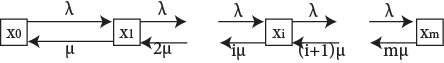
Протекающий процесс является процессом гибели и размножения. Финальные вероятности состояний существуют и находятся по формулам:

 -
приведенная интенсивность потока заявок
(загрузки канала)
-
приведенная интенсивность потока заявок
(загрузки канала)
С учетом введенных обозначений формулы предельных вероятностей имеют вид:

Показатели эффективности:
1)
2)относительная
пропускная способность

3)абсолютная
пропускная способность

4)среднее число занятых каналов

30. Одноканальные системы массового обслуживания с ожиданием и ограничением на длину очереди.
СМО с 1каналом, на вход которой подается прост. поток заявок интенсивностью λ. Поток обслуживания также является простейшим, и его интенсивность равна μ. Предполагается, что в данной системе имеется ограничения на длину очереди, под кот. понимается мах число мест для ожидания обсл-ния n>=1 Заявка, поступившая в момент, когда канал обслуживания занят и свободных мест в очереди нет, получает отказ и покидает очередь необслуж. Требуется определить параметры функционирования СМО. x0 – канал свободен, 0 заявок в системе, очереди нет. x1 –1 заявка в системе, канал занят, 0 заявок в очереди. x2 – 2 в системе, канал занят, 1 заявка в очереди.…xn+1 – n+1 заявка в системе ,канал занят, n заявок в очереди.
![]()
![]() => αi
=> αi =>
=>
![]()
![]() .
.
При λ = μ p0 = p1 = … = pn+1 = 1/(n + 2) .
При
![]()
![]()
Показатели:
Вер-ть отказа:
![]() ;
или 1/n+2
;
или 1/n+2
Относительная пропуская способность:
![]() -
или n+1/n+2
-
или n+1/n+2
Абсолютная пропускная способность:
![]() ;
;
Ср число заявок, находящихся в очереди:Введем сл.вел. Nоч –кол-во заявок, нах-ся в очереди – дискретного типа
![]() …=
…=![]()
Количество заявок, поступивших в систему – вел-на дискр.типа задается рядом распред.
Nобсл 0 1
Ве-ть p0 1-p0
Nобсл =0*po+1(1-po)=1-po=…
![]() или
n+1/n+2
или
n+1/n+2
Общее число заявок в системе
![]()
Важной
хар-кой одноканал СМО явл. Ср.время
ожидания в очереди -
![]() =
M(Tоч)
=
M(Tоч)
Среднее
время нахождения
заявки в системе и в очереди находится
по формулам Литтла: