26. Процессы гибели и размножения, финальные вероятности состояний.
Марковский процесс, протекающий в системе с конечным числом состояний в непрерывном времени называется процессом гибели и размножения, если его размеченный граф имеет вид:
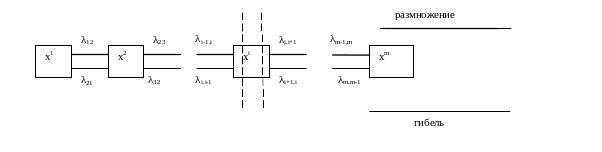
Особенность
процесса проявляется также в том, что
матрица плотностей вероятности является
ленточной. Вероятности состояний pi(t),
определяющие эволюцию системы как
систему дифференциальных уравнений
Колмогорова:
;
;
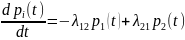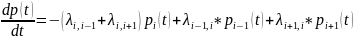
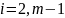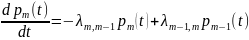
Процесс
гибели и размножения как и всякий
Марковский процесс имеет свойство
стабилизироваться, в том смысле, что
вероятности состояний стремятся к их
стационарным (предельным) состояниям:
.
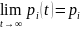Утверждение:
Если в системе
с конечным множеством состояний протекают
процессы гибели и размножения, то
финальные вероятности состояний
существуют и находятся по формулам:
.
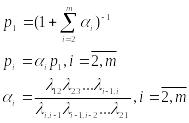Числитель – произведение наддиагональных элементов. Знаменатель - произведение поддиагональных элементов.
Финальные вероятности состояний находятся из системы у-ний, матрица которой имеет вид (пишем системы, обнуляя левые части и добавляя константы).
Матрица (коэффициентов при неизвестной) отвечает данной системе:
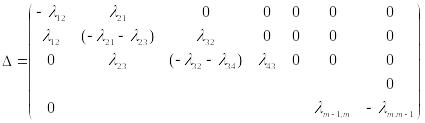II
+ I
строки
Решаем систему методом исключения Гаусса, преобразуя матрицу с помощью эквивалентных действий.
1) Первое уравнение оставляем без изменений;
2) Ко второму уравнению добавляем первое;
3) К третьей строчке добавляю новую вторую;
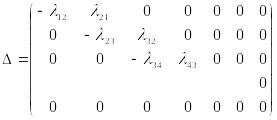
Убираем последнее уравнение и добавляем нормировочное равенство.
Записываем систему уравнений, отвечающую последней матрице:
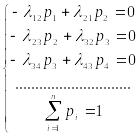
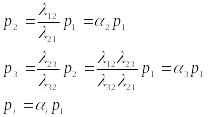
Получившееся
выражение подставим в последнее
нормировочное равенство: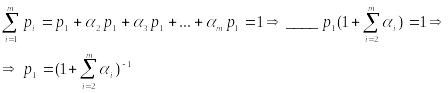
Иногда состояния системы целесообразно нумеровать не с 1 , а с 0. В этом случае расчетные формулы для вероятностей записываются в виде:
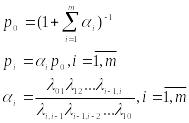
27. Процессы гибели и размножения в системе с m узлами, финальные вероятности состояний.
Имеется
система с м узлами, каждый из который
может выходить из строя независимо от
других: на каждый узел действует
пуасоновский поток отказов, событие –
отказ узла. Среднее время безотказной
работы узла -
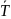б.
Целесообразно рассматривать весь поток,
т.к. можно говорить о его интенсивности.
Отказавший узел сразу ремонтируют. На
узел действует простой поток восстановлений,
событие – конец ремонта. Среднее время
восстановления:
в.
Система – совокупность м узлов, ее тек
состояние определяется кол-вом работающих
и ремонтирующихся узлов: х0-
0 в ремонте, м исправно; х1-
1 в ремонте, (м-1)-исправен. интенсивность
потока отказов, действующих на один
узел - λ=(
б)-1,
µ=(
в)-1
Финальные вер-ти могут быть найдены по
общим формулам: p0=(1+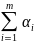
)-1,
pi=αip0,
αi=
.
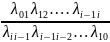На практике финальные вер-ти удобнее
выражать через
б
и
в.
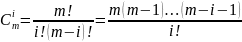
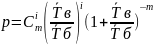
28. Системы массового обслуживания, их основные компоненты и характеристики функционирования.
Теория массового обслуживания представляет собой основы комплекса вопросов эффективности конструирования и эксплуатации систем массового обслуживания. Системы массового обслуживания – это системы специального вида, реализующие многократное выполнение достаточно однотипных задач. Примерами СМО в экономической сфере являются банки различного типа, страховые компании, налоговые инспекции, системы связи, погрузочно-разгрузочные комплексы и тд.
Основными элементами модели массового обслуживания являются клиенты (заявки или требования, которые в совокупности формируют поток заявок). Клиенты поступают в систему обслуживания из источника. Источник генерирующий клиентов, подлежащих обслуживанию, может иметь конечную или бесконечную мощность. Источник конечной мощности ограничивает количество клиентов, поступающих в систему. Источник бесконечной мощности всегда имеет клиентов в изобилии.
Клиенты поступают на сервис (обслуживающее устройство, которое может состоять из одного или нескольких физических обслуживающих единиц, которые называются каналами обслуживания). Поступив в сервис клиенты могут сразу попасть на обслуживание или ожидать в очереди, если сервис занят. При наличии очереди после завершения процедуры обслуживания сервис автоматически выбирает клиента, чтобы приступить к его обслуживанию. Если очередь отсутствует, сервис остается не занятым до прибытия нового клиента. Поступление клиентов характеризуется интервалом времени между двумя последовательными поступлениями, а обслуживание временем обслуживания клиента, или (что тоже самое) интенсивностью потока поступлений и потока обслуживания соответственно. Важным фактором при анализе систем СМО является дисциплина очереди или принцип построения, определяющий порядок в соответствии с которым клиенты выбираются из очереди. В совокупности с длиной очереди дисциплина очереди формирует дисциплину обслуживания.
При анализе СМО имеет значение также поведение человека, нуждающегося в обслуживании. Такие индивиды, выступающие в роли клиентов, при наличии многоканального обслуживания, могут перейти из одной очереди в другую, тем самым изменив дисциплину очереди. Они также могут сразу отказаться от обслуживания или покинуть систему, находившись в ней определенное время.
Цель теории массового обслуживания – это разработка рекомендаций по рациональному построению СМО, рациональной организации их работы и регулированию потока заявок для обеспечения высокой эффективности функционирования СМО.
В качестве характеристик функционирования и эффективности используются два набора показателей.
Параметры функционирования СМО
абсолютная пропускная способность – А – это среднее число заявок, которое обслуживается системой в единицу времени.
относительная пропускная способность – Q – это отношение среднего числа заявок, обслуженного системой в единицу времени к общему числу заявок, находящемуся в системе в единицу времени или вероятность того, что заявка, поступившая в систему будет обслужена.
средняя продолжительность периода занятости СМО, то есть та часть времени, в которую СМО занято обслуживанием заявок
среднее число занятых каналов
Параметры качества обслуживания
среднее время
среднее время пребывания заявки в системе
вероятность того, что заявка покинет систему необслуженной
вероятность того, что поступившая в систему заявка немедленно будет принята на обслуживание
среднее число заявок, находящихся в очереди
среднее число заявок, находящихся в системе