24. Вероятностные характеристики простейшего потока.

Пусть имеется пуассоновский поток интенсивности 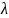, свяжем с ним случайную величину 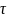– число событий, появившихся в потоке за временной интервал (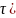 . В силу стационарности потока характеристики этой величины зависят лишь от длины промежутка и не зависят от точки его приложения. Основной характеристикой этой случайной величины является вероятность того, что случайная величина х от принимает значение m.

P(X(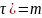 )=P_m(

1. Вероятность того, что за время в потоке не появится ни одно событие

P(X( )=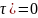

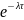
2. Вероятность того, что за время в потоке появится хотя бы одно событие, то есть временной интервал не останется пустым

P(X(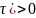 )=P(X( )>=1)

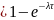
3. Вероятность того, что за время в потоке появится не более k событий

P(X( )=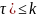

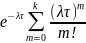
4. Вероятность того, что в потоке появится более k событий

P(X( )=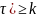

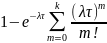
5. Интенсивность потока есть мат ожидание случайной величины x от 1

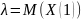
MX(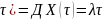

Элементом вероятности появления событий в потоке 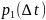называется вероятность того, что за достаточно малый промежуток времени дельта t в потоке появится хотя бы одно событие. Для элемента вероятности справедливо асимптотическое равенство.

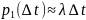
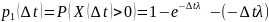
Другой характеристикой случайного потока является случайная величина T – время между двумя последовательными событиями потока. Для случайно величины T, характеризующей пуассоновский поток справедливо следующее утверждение:

1. Интегральная функция распределения случайной величины T

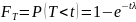
2. Дополнительная функция распределения

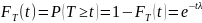
3. Дифференциальная функция распределения

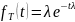
4. Мат ожидание случайной величины T

MT=1/

5. ДT = 1/

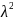
25. Роль экспоненциального распределения в исследовании простейших потоков. Финальные состояния системы, в которой протекает марковский процесс.

Элементом вероятности в пуассоновском потоке событий интенсивности называется вероятность появления события в потоке за малый промежуток времени ∆t.

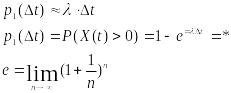
Это второй замечательный предел. Следствие из него:

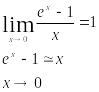(эквивалентность)

Пусть в системе с конечным множеством состояний {X₁, X₂, …, X_n} протекает Марковский процесс с непрерывным временем, причем переход из состояния в состояние осуществляется под действием пуассоновского потока. Последнее следует понимать так: если в некоторый момент времени t₀ система находилась в состоянии x_i, то после того, как в потоке появилось первое случайное событие, система перешла в состояние x_j не равное x_i:

Утверждение: Плотности вероятностей переходов из состояния в состояние равны интенсивности потока, под действием которого осуществляется переход: λ_ij = λ.

Доказательство:

Если все потоки, переводящие систему, являются пуассоновскими и поэтому процесс является марковским, вероятности его состояний стабилизируются во времени, т.е. сущ. пределы: lim p_i(t)= p_i ; t → ∞

Финальные вероятности состояний можно интерпретировать как среднее относительное время пребывания системы в каждом состоянии. Последнее понимается таким образом: - время пребывания системы в состоянии xi; случ. Величина; = - среднее время пребывания в xi, - среднее время пребывания системы вне состояния xi, - среднее время функционирования системы.

Пред. вероятности характеризуются тем, что их производные равны 0.

Финальные вероятности находятся как решение системы линейных алгебраических уравнений, полученной из системы дифференциальных уравнений Колмогорова обнулением левой части.

; - числа;

Это вырожденная система, поэтому для ее решения нужно добавить нормировочное равенство: