22. Случайные процессы с непрерывным временем, их формализация. Система дифференциальных уравнений Колмогорова, правила ее составления.

Переход из состояния x в состояние может осуществиться в любой момент времени. Обозначим Xi(t) – случайное событие, система в момент времени t находится в состоянии i.

P(Xi(t))=pi(t) – функция времени, а не этапа, переходные вероятности.

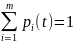
Введем обозначения:

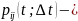вероятность того, что система, находившаяся в момент t в состоянии xi за временной промежуток [t,t+дельта t). Эта вероятность может быть равна нулю в одном из трех случаев:

1. в момент времени t система находилась в состоянии xi и находилась в нем на протяжении всего рассматриваемого временного промежутка;

2. в момент t система находилась в xi, но за рассматриваемый промежуток перешла в другое состояние, отличное от xj;

3. В момент времени t система не находилась в состоянии xi.

Во всех других случаях вероятность строго положительна, однако стремится к нулю при дельта t стремящемся к нулю.

Предел отношения

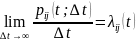
Из определения следует, что плотности вероятностей перехода могут принимать любое неотрицательное значение в том числе и больше 1.

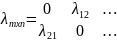
Граф состояний системы, дуги которого нагружены плотностями переходных вероятностей называется размеченным графом системы.

Из определения следует асимптотическая формула:

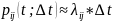
Вероятности состояний системы могут быть найдены как решения нормальной системы дифференциальных уравнений следующего вида:

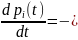i=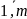

Первое правило составления системы Колмогорова:

1. Для того, чтобы составить i-е уравнение системы в левой его части следует записать производную 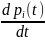. Справа произведение суммы плотностей вероятностей дуг, исходящих из i-го состояния на вероятность этого состояния, взятое со знаком минус и добавить к нему сумму парных произведений плотностей вероятностей дуг, входящих в i-е состояние и вероятностей состояний, из которых осуществляется переход в xi.

2. Второе правило по матрице плотности. Справа – сумма элементов i-й строки матрицы 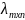умноженная на вероятность i-го состояния и это произведение берется со знаком минус. Со знаком плюс, каждый элемент i-го столбца умножается на вероятность состояния одноименного номеру строки и эти произведения берутся со знаком плюс. Решение системы Колмогорова находится методами теории обыкновенных дифференциальных уравнений.

Нормальная система диф уравнений имеет вид:

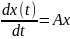
Решением системы называется n-ка функций, которая при подстановке в систему обращает каждое ее уравнение в верное числовое равенство.

Общим решением x(t) называется вектор функции, зависящий от аргумента t и n произвольных состояний, которая является решением системы при любом конкретном выборе значения произвольных состояний.

23. Потоки событий, их свойства. Простейший (пуассоновский стационарный) поток.

Поток событий – последовательность случайных событий, следующих одно за другим в некоторые моменты времени. Поток событий называется однородным, если входящие в него события различаются только по моментам времени, неоднородным – в противном случае. Поток называется регулярным, если события в нем наступают через строго определенные промежутки времени. Поток событий называется потоком без последействия (без памяти), если для любой пары непересекающихся промежутков времени число событий на одном промежутке не зависит от числа событий на другом промежутке времени. Поток событий называется ординарным, если для любого достаточно малого промежутка времени вероятность наступления за этот промежуток двух и более событий потока пренебрежимо мала по сравнению с вероятностью наступления не более одного события.

Поток событий называется стационарным, если вероятность наступления случайного события за некоторый промежуток времени зависит только от длины промежутка, но не зависит от момента его начала. Поток событий называется простейшим или пуассоновским, если он одновременно является ординарным, стационарным и не имеет последействия. Интенсивностью потока событий называется среднее число событий в потоке в единицу времени: inП=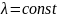 . Пуассоновские потоки обладают следующим свойством: при наложении n пуассоновских потоков с сопоставимыми интенсивностями λ_i возникает пуассоновский поток, интенсивность которого равна сумме частных интенсивностей: