20.Марковские процессы принятия решений с бесконечным числом этапов: специфика постановки задачи. Отыскание оптимальных стратегий на бесконечном временном горизонте методом полного перебора.

На бесконечном временном горизонте в форме максимизации полного ожидаемого дохода смысла не имеет: он автоматически становится бесконечным, нужно делать дополнительные предположения о стабилизации процессов. Марковские процессы и обладают тем свойством, что стабилизируются с течением времени. Последнее проявляется в том, что вероятности состояний стремятся к некоторым пределам, после чего система функционирует в установившемся режиме.

При определении оптимальной долгосрочной стратегии марковская задача принятия решений может основываться на оценке результата за переходный период. Однако более естественной является постановка задачи в форме оптимизации результата за один период после того, как система перешла в установившейся режим. Рассматриваются лишь стационарные стратегии, когда выбор управляющего воздействия не зависит от номера этапа, а опр лишь текущим состоянием системы.

Существует два основных метода решения задач с бесконечным временным горизонтом. Первый основан на переборе всех стационарных стратегий. Однако использовать его можно лишь при небольшом числе состояний системы и, как следствие, небольшом количестве стационарных стратегий. При использовании второго метода (итеграции по стратегиям) возникают вычислительные сложности.

Метод полного перебора

Суть: рассматриваются все возможные стационарные стратегии. Каждая из них количественно оценивается средним ожидаемым результатом за один период, сопоставлением найденных оценок выбирается способ действия.

Q – стац стратегии

P^q,R^q – матрицы переходных вероятностей и результатов.

Действие алгоритма сводится к 4 шагам:

1. По заданным матрицам Pq и Rq находят средний ожидаемый доход за один этап для каждого i-ого состояния системы.

V_i^q=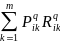

2. По данной матрице находим финальные состояния системы из матричного уравнения системы P^{q q}= ^q, ^q=( ^q_{1, 2}^q….)

3. находят ожидаемый выигрыш за i – этап: E^q. 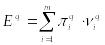После выполнения этого алгоритма для всех стационарных стратегий получают набор Е¹, Е², …, Е^q ожидаемых результатов, из которых и выбирается оптимум.

4. Сопоставляем оценки, выбираем

21. Метод итераций по стратегиям без дисконтирования (для бесконечного числа этапов).

При рассмотрении метода динамического программирования на конечном числе этапов была получена формула, позволяющая оценить каждую стационарную стратегию с номером q.

Для того, чтобы применить эту формулу на бесконечном временном горизонте необходимо несколько модифицировать ее. Пусть eta количество этапов, которые остались для анализа

В полной теории марковских процессов установлено, что приближенно находится

Алгоритм Ховарда состоит из двух последовательно повторяемых шагов.

Шаг 1 – этап оценивания параметров. Выбрать произвольно стационарную стратегию с номером q в качестве начальной. Используя матрицы , отвечающие данной стационарной стратегии составить систему линейных уравнений.

Эта система является неопределенной, в том смысле, что содержит m уравнений и m+1 переменную. Для того, чтобы замкнуть систему одну из переменных выбирают произвольно. Обычно полагают остальные значения из системы находятся однозначно.

Шаг 2 – улучшение стратегии. Для каждого состояния системы xi находим управленческую альтернативу U, обеспечивающую оптимум opt{ } где в качестве f^q(x_k) берется значение, полученное на шаге оценивания параметров.

В совокупности найденные управленческие альтернативы формируют новую стационарную стратегию. При совпадении двух последовательно полученных стационарных стратегий, она и считается оптимальной. В противном случае переходят к шагу один с новой стационарной стратегией.

Шаг 3: Если 2 последовательные стационарные стратегии совпали, то найдется стационарная стратегия, являющаяся оптимальной. В противном случае полагается q=t и переходят к шагу 1 с новой стационарной стратегией.