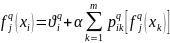18. Марковские процессы с дискретными состояниями. Формула Колмогорова-Чепмена.

Процессы с дискретным временем и дискретными состояниями называются марковскими или цепями маркова.

Процессы с дискретными состояниями; X(t) если каждое его сечение представляет собой случайную величину дискретного типа с конечным или счетным множеством состояний. Процессы с дискретными состояниями обычно изображаются в форме графов, вершины которых соответствуют возможным состояния системы, а дуги показывают непосредственные переходы из одного состояния в другое.

Основными характеристиками цепей маркова являются вероятности состояний pi(n). Вероятности того, что в момент времени tn система перешла в i-ое возможное состояние.

Предполагается, что состояния системы определены таким образом, что в каждый момент времени система находится ровно в одном из своих возможных состояний.

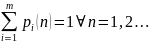
Для вычисления вероятности состояний вводится понятие переходных вероятностей.

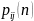
Это вероятность того, что система, находящаяся в i-ом состоянии переходит в свое j- ое состояние. P_ii(n) – вероятность задержки.

Если непосредственный переход из одного состояния невозможен. То переходная вероятность полагается равной 0. Если переходные вероятности зависят от номера этапа, марковская цепь называется неоднородной. В противном случае – однородной.

P_mxm=(pij) – матрица переходных вероятностей, элементы которой удовлетворяют нормировочному равенству

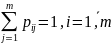
Граф состояний системы, дуги которого нагружены вероятностями перехода, называется размеченным графом системы.

p(0)=(p1(0),p2(0)…) компоненты которого показывают вероятности состояний системы в начальный момент времени называют вектором абсолютных вероятностей. Динамика цепи Маркова определяется вектором абсолютных вероятностей и матрицей переходных вероятностей.

p(1)=p(0)*P

p(n)=p(o)*Pⁿ

Это формулы Колмогорова – Чепмена

19. Марковские процессы принятия решений с конечным числом этапов: метод итераций по стратегиям и его возможные обобщения.

Пусть имеется некоторая система S, текущее состояние которой представлено элементом из конечного множества состояний, а процесс ее функционирования и процесс принятия решения разбивается на отдельные этапы. Переходные вероятности между состояниями описываются МЦ с матрицей Рm*M=(pij). Каждый одношаговый переход сопровождается некоторым результатом r_ij (доходами, затратами), которые в совокупности образуют матрицу одношаговых результатов R=( r_ij). Величина результата определяется выбранным управлением на каждом шаге и в каждом состоянии, т.е. матрица переходных вероятностей и результатов зависит от вариантов решений, которыми располагает ЛПР. Цель - определение оптимальной стратегии, максимизирующей ожидаемый доход или минимизирующей затраты.

Хар-р задач, стоящих перед ЛПР, зависит от горизонта планирования. Если деятельность ЛПР определяется конечным числом этапов, то наиболее естественным подходом является оптимизация результата за n шагов. опр-ся вероятностными связями МЦ и выбранным управлением и называется полным ожидаемым результатом.

ЛПР может интересовать оценка полного ожидаемого результата при заранее определенной стратегии поведения в случае одного и того же состояния системы, не зависящего от № этапа. Такая стратегия называется стационарной. Если все стационарные стратегии известны, то оценив каждую из них, можно выбрать наилучший способ действия. Однако такой подход применяется преимущественно на бесконечных временных горизонтах. При конечном горизонте планирования пользуются более экономными методами, основанными на идеях динамического программирования.

Метод динамического программирования с конечным числом этапов

Uj=1 – используем рекламу, =0 – нет.

F*j(xi) – полный ожидаемый максимальный результат за период j, j+1….n, если к началу j-ого этапа система находилась в состоянии xi.

F^*_j(x_i)=max_u=1,0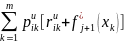

V_i^u-ожидаемый одношаговый результат, если система находится в состоянии x_i.

F^*_j(x_i)=max_u=1,0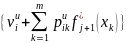

Рассмотренная задача на конечном временном горизонте может быть обобщена в следующих направлениях:

1.Переходные вероятности и значения результата необязательно должны быть одинаковыми на каждом этапе. Можно потребовать, чтобы эти параметры зависели от номера этапа, то есть Марковская цепь была неоднородной.

2.Учитывая, что ожидаемые результаты относятся к разным временным периодам, целесообразно вводить коэффициент дисконтирования. В следствии чего значения функции f будут представлять приведенные величины ожидаемых доходов по всем этапам. Формально это обобщение вводится следующим образом. 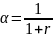тогда

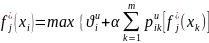
3.Записанное рекуррентное уравнение можно использовать и для оценки произвольной стационарной оценки с номером q.