Y

1. Парето-оптимальные решения многокритериальных задач и способы сужения границы Парето: субоптимизация, лексикографическая оптимизация, построение обобщенного критерия. 2

2. Метод анализа иерархий (метод Саати): определение значимости критериев, согласованность матрицы парных сравнений, определение весовых коэффициентов методом собственного вектора. 3

3. Критерии принятия решений в условиях неопределенности: методы Лапласа, Вальда, Сэвиджа, Гурвица. 4

4. Обобщенный критерий Гурвица для безопасной и опасной ситуаций. 5

5. Понятие ситуации риска, основные постулаты риск-менеджмента, формализация ситуации риска, принципы доминирования. 6

Риск – это возможность ненаступления некоторых ожидаемых событий и возможность отклонения каких-либо величин от их ожидаемых расчетных значений. Экономический риск представляет собой неоднозначность экономических результатов хозяйствующего субъекта в будущем, обусловленную неоднозначностью самого этого будущего. 6

Формализация ситуации риска, принципы доминирования. 6

6. Меры риска, масштабные и вероятностные. 7

7. Критерии принятия решений в условиях риска: ожидаемого значения (критерий Байеса), минимальной вариации, предельного уровня, наиболее вероятного исхода. 8

8. Критерий «ожидаемое значение – вариабельность результата», коэффициент склонности к риску, зоны склонности к риску. 8

9. Понятие кривой безразличия. Три типа кривых безразличия. 8

10. Понятие идеального эксперимента, обоснование его целесообразности. 9

11. Понятие неидеального эксперимента, алгоритм обоснования его целесообразности. 10

12. Смешанные стратегии как инструмент уменьшения риска. 10

13. Понятие функции полезности, алгоритм ее построения. Основные типы функций полезности. 11

14. Интенсивность несклонности к риску, премия за риск (подход Марковица). 13

15. Формула Эрроу-Пратта. 13

16. Понятие многошагового управляемого процесса. Формализация многошаговой детерминированной задачи принятия решения. 14

17. Характерные особенности многошаговых процессов принятия решений. Принцип оптимальности Беллмана. 15

18. Марковские процессы с дискретными состояниями. Формула Колмогорова-Чепмена. 15

19. Марковские процессы принятия решений с конечным числом этапов: метод итераций по стратегиям и его возможные обобщения. 16

20.Марковские процессы принятия решений с бесконечным числом этапов: специфика постановки задачи. Отыскание оптимальных стратегий на бесконечном временном горизонте методом полного перебора. 17

21. Метод итераций по стратегиям без дисконтирования (для бесконечного числа этапов). 17

22. Случайные процессы с непрерывным временем, их формализация. Система дифференциальных уравнений Колмогорова, правила ее составления. 18

23. Потоки событий, их свойства. Простейший (пуассоновский стационарный) поток. 19

24. Вероятностные характеристики простейшего потока. 19

25. Роль экспоненциального распределения в исследовании простейших потоков. Финальные состояния системы, в которой протекает марковский процесс. 20

26. Процессы гибели и размножения, финальные вероятности состояний. 21

27. Процессы гибели и размножения в системе с m узлами, финальные вероятности состояний. 22

28. Системы массового обслуживания, их основные компоненты и характеристики функционирования. 22

29. Многоканальные системы массового обслуживания с отказами. 23

30. Одноканальные системы массового обслуживания с ожиданием и ограничением на длину очереди. 24

1. Парето-оптимальные решения многокритериальных задач и способы сужения границы Парето: субоптимизация, лексикографическая оптимизация, построение обобщенного критерия.

Математически ЗПР при многих критериях в строго детерминированной ситуации задается картежом: <A, (f₁, f₂, …, f_m)>; f_i – функция, количественно характеризующая i-тый критерий. Для каждого локального критерия K_i и выражающей его функции f_i рассмотрим множество оценок по этому критерию:

Y – множество векторных оценок А, и на этом множестве вводится бинарное отношение доминирования по Парето. Говорят, что векторная оценка доминирует по Парето :

если и существует такой i:

Множество недоминируемых по Парето векторных оценок составляет Парето оптимальное множество или границу Парето: Отношение доминирования по Парето переносится непосредственно на сравниваемые А. Говорят, что Аа из множества А доминирует А а’ из множества А по Парето, если векторная оценка Аа доминирует по Парето векторную оценку Аа’:

Недостаток критерия Парето состоит в том, что он незначительно сокращает множество возможных исходов и как следствие допустимых альтернатив.

Методы сокращения/суждения Парето – оптимального множества

1.Задание пороговых значений критериев. Исходная оптимальная задача заменяется задачей поиска А , удовлетворяющей системе неравенств:

_; γ_i – пороговое значение соответственного критерия, которое не может быть ухудшено.

«-» не позволяет отыскать единственное решение, а лишь отбирает приемлемые варианты, оценка которой по всем критериям превосходит установленные пороги.

2.Субоптимизация, сокращение границы Парето. Один из критериев, например, 1-ый, объявляется главным, а остальные переводятся в разряд ограничений:

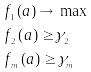
3. Лексикографическая оптимизация. Предполагался, что все локальные критерии ранжированы по их значимости (упорядочены). Сначала рассматривается задача оптимизации по наибольшему значимому критерию. Если А стремится к мах значению и эта А единственна, то она и принимается в качестве оптимальной. Если таких А несколько, то на множестве, составленном из них, рассматривается задача максимизации. Если А конечное число, то за конечное число шагов будет выбрана опт. А.

Методы построения обобщенного критерия, свертки критериев – процедура, которая агрегирует набор оценок по заданным локальным критериям в итоговую числовую оценку, выражающую совокупную ценность этого набора для ЛПР. Обобщенный критерий задаётся функцией, сохраняющей исходную упорядоченность альтернатив (лучшим альтернативам соответствует большие значения обобщенного критерия). Задание обобщенного критерия превращает многокритериальную задачу в задачу одномерной оптимизации. Обобщенный Критерий не позволяет в полной мере использовать всю инфу, которая имеется в векторной оценке. Частные критерии оценки проекта можно разделить на 2 группы: критерии отражающие результат и критерии связанные с затратами. Предположим, удалось построить обобщенный показатель рез-та R и обобщенный показатель затрат С. Обобщенной оценкой проекта может служить показатель эффективности: . Обобщенные критерии обычно строятся в форме свёрток:

1)максимин свёртка: (подтянем худшего). На практике чаще пользуются нормированной свёрткой, когда задаются эталонные значения для каждого критерия и отклонения от этих эталонов минимизируется

2)Мультипликативная свёртка . Используется когда все локальные критерии критически важны для ЛПР и обращение в 0 хотя бы одного из них лишает смысла весь результат.

3)Аддитивная свёртка