Федеральное агенство по образованию
Министерство образования и науки Российской Федерации
Санкт-Петербургский государственный университет
технологии и дизайна
кафедра инженерной химии
и промышленной экологии
Курсовая работа
по дисциплине
Математическое моделирование сложных хтс и их элементов
Студент: Чуркова Е.А.
Группа: 4-хд-2
Преподаватель: Багров И.В.
Санкт-Петербург 2012 год
Содержание
Задание.
1)Рассчитать расходы выходных и всех промежуточных потоков данной разомкнутой ХТС :
4
11
12
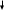
1
2
3
5
6
7
8
9
10
G01=1800, G05=2000, G09=3000, G011=4000, K51=0.5, K67=0.4, K73=0.2, K84=0.45, K117=0.6, K128=0.45
2
)Рассчитать
расходы выходного и всех промежуточных
потоков данной замкнутой ХТС :
1
2
3
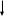
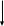
6
4
5
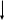
G01=1000, G04=8000, G02=1500, K21=0.3, K23=0.3, K30=0.3, K25=0.4, K54=0.1, K65=0.2
Расчет материальных и тепловых потоков в сложных ХТС.
Постановка задач и методы расчета ХТС.
ХТС- совокупность взаимосвязанных техническими потоками и действующих, как одно целое аппаратов, в которых осуществляется определённая последовательность технических операций.
Также под ХТС понимают совокупность физико-химических процессов и средств для их проведения с целью выделения в нужном количестве, соблюдение экологических норм и норм надёжности, числом и составом элементов.
Для нахождения параметров состояния выходных и промежуточных потоков технологической системы при известных заданных параметрах входных потоков , а также конструктивных характеристик аппаратов и узлов, используют следующие методы :
Интегральные - объединение систем уравнений , описывающих работу отдельных аппаратов , в одну большую систему уравнений и решения этой системы. Однако главный недостаток этой группы методов- большая размерность единой системы уравнений и уникальность каждой системы уравнений.
Декомпозиционные – каждый аппарат или группу аппаратов рассчитывают отдельно, а расчёт всей ХТС заключается в последовательном расчёте аппаратов и узлов.
Автоматизированные системы технологических расчётов и моделирующие программы для расчёта сложных ХТС базируется в основном на декомпозиционном методе.
Расчет разомкнутой ХТС.
Расчёт разомкнутой ХТС основан на декомпозиционнном методе расчёта , основной задачей которого является определение последовательности расчёта аппаратов.
Формальные подходы к определению последовательности расчёта базируются на представлении структуры ХТС в виде графов и таблиц.
Изображение ХТС в виде ориентированного графа.
Вершины графа соответствуют аппаратам, а дуги потокам. Последовательность сцепленных дуг, позволяющая пройти от одной вершины к другой , называется путём.
1 2 3 4 5 6 7 8 9 10 11 12
Информация, содержащаяся в графе может быть представлена в виде различных матриц, что позволяет перевести графическую информацию в числовую и разработать математические методы анализа ХТС.
Определение вычислительной последовательности расчета системы (ВПРС) по матрице смежности
Матрица смежности - это квадратная матрица, число строк и столбцов равно числу вершин графа. В первой строке единицей в соответствующем столбце отмечаем наличие потоков от 1го аппарата к другим элементам схемы, во второй строке – от второго аппарата и т.д.
[A]=
Нулевой столбец указывает на входную вершину или аппарат, который может быть сразу рассчитан, нулевая строка указывает на выходной элемент или аппарат - он рассчитывается последним. Так как расчёт входного аппарата приведён к определению параметров его выходных потоков , связи этого аппарата с другими элементами схемы будут известны , т.е. после включения в ВПРС входной вершины можно вычеркнуть из дальнейшего рассмотрения соответствующую строку и столбец матрицы смежности и анализировать далее оставшуюся часть матрицы.
ВПРС: 9,11,10,12,6,5,7,1,2,3,8,4.
Определение ВПРС по списку смежности
Исходя из принципа заполнения списка смежности, выходной будет вершина, номер которой находится только в правом столбце, входной - номер которой будет встречаться только в левом столбце выходов. По аналогии с предыдущим методом включение вершины в ВПРС позволяет включить её связи из списка смежности.
1 |
3 |
2 |
3 |
3 |
4 |
5 |
1 |
5 |
2 |
6 |
5 |
6 |
7 |
7 |
3 |
7 |
8 |
8 |
4 |
9 |
6 |
10 |
6 |
11 |
7 |
11 |
10 |
11 |
12 |
ВПРС: 9,11,10,12,6,5,7,1,2,3,8,4
Определение ВПРС по матрице связей
Вершина графа |
Вершина из кот. поступает поток |
Число неизвестных, входящих в элемент на каждом графе |
||||||
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
0,5 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
2 |
5 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
3 |
1,2,7 |
3 |
3 |
3 |
3 |
2 |
0 |
0 |
4 |
3,8 |
2 |
2 |
2 |
2 |
2 |
2 |
0 |
5 |
0,6 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
6 |
9,10 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
7 |
6,11 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
8 |
7,12 |
2 |
2 |
1 |
1 |
0 |
0 |
0 |
9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
10 |
11 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
12 |
11 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
ВПРС: 9,11,10,12,6,5,7,1,2,3,8,4
После определения последовательности расчёта аппаратов, необходимо составить математическое описание.
Математическое описание и расчет разомкнутой ХТС
9
G 09 G96
G96=G09
G96=3000
11
G 011
G1110=0.2*G011
G1110=0.2*4000=800
G117=0.6*G011
G117=0.6*4000=2400
G1112=0.2*G011
G1112=0.2*4000=800
10
G 1110 G106
G106=G1110
G106=800
12
G 1112
G128=0.45*G1112
G128=0.45*800=360
G120=(1-0.45)*G1112
G120=0.55*800=440
G
6
96 G65G 106 G67
G65=(1-0.4)*(G96+G106)
G65=0.6*(3000+800)=2280
G67=0.4*(G96+G106)
G67=0.4*3800=1520
G
5
05 G51G 65 G52
G51=0.5*(G05+G65)
G51=0.5*(2000+2280)=2140
G52=0.5*(G05+G65)
G52=2140
G
7
67 G73G 117 G78
G73=0.2*(G67+G117)
G73=0.2*(1520+2400)=784
G78=0.8*(G67+G117)
G78=0.8*3920=3136
G
1
01 G13G 51
G13=G01+G51
G13=1800+2140=3940
G
2
52 G23
G23=G52
G23=2140
G
3
13G 23 G34
G73
G34=G13+G23+G73
G34=3940+2140+784=6864
G
8
78 G84G 128 G80
G84=0.45*(G78+G128)
G84=0.45*(3136+360)=1573.2
G80=0.55*(G78+G128)
G80=0.55*1922.8
G
4
34 G40G 84
G40=G34+G84
G40=6864+1573.2=8437.2
Расчет математического описания в Mathcad
Проверка: приход равен расходу
Материальный баланс соблюдается, расчёт произведён верно.