9.5. Частотные характеристики динамических звеньев

Е сли входной сигнал САУ изменяется по гармоническому закону заданной амплитуды и частоты, то нахождение параметров колебаний на выходе САУ легче осуществлять с помощью частотных характеристик. Пусть гармонический входной сигнал с амплитудой и фазой проходит через устойчивое звено. На выходе звена сигнал смещается по фазе и имеет другую амплитуду (рис. 9.11). Искажённый вид начального участка выходного сигнала объясняется влиянием переходного процесса

Если в передаточной функции заменить на , то частотную передаточную функцию звена можно представить в следующем виде: ,

где ; .

Кроме того, , где ; .

Функция называется амплитудной частотной характеристикой (а.ч.х.).

Функция называется фазовой частотной характеристикой (ф.ч.х.) звена.

Функция называется вещественной частотной характеристикой звена.

Функция – мнимая частотная характеристика звена.

Для каждого фиксированного значения частотная передаточная функция на плоскости может быть изображена вектором , отклонённым от положительного направления оси абсцисс на угол . Годограф этого вектора при изменении частоты от до называется амплитудно-фазовой частотной характеристикой звена (рис. 9.12).

– действительная часть комплексного числа , ( – действительный (франц.))

– мнимая часть комплексного числа , ( – мнимый (франц.))

– аргумент комплексного числа , (это угол , измеренный в радианах) – применяется при тригонометрической форме записи комплексного числа.

9.6. Логарифмические частотные характеристики линейных звеньев

Частотные характеристики, построенные в логарифмических шкалах, называются логарифмическими частотными характеристиками. При построении логарифмических характеристик на шкале частот, например, вместо откладывают . Это существенно упрощает исследование линейных САУ.

9.7. Типовые динамические звенья и их характеристики

Типовыми динамическими звеньями называются звенья, описываемые дифференциальным уравнением не выше второго порядка (в переменных вход и выход). Эти звенья классифицируют в зависимости от вида левой и правой частей их дифференциального уравнения. Все типовые звенья разделяют на три группы: позиционные, интегрирующие и дифференцирующие. Каждая из групп содержит несколько типовых звеньев (табл. 9.1). К сожалению названия звеньев и их количество пока не одинаковы у разных авторов .

Т

Передаточная функция W(s)

аблица 9.1

№ п.п.	Груп-па	Тип звена	Вид дифференциального Уравнения
1	Пози-цион-ные	Безинерционное (пропорциональное)	y = ku	k
2		Апериодическое 1-го порядка (инерционное)	(Tp + 1) y = ku
3		Апериодические 2-го порядка	( T2p2+2ξTp+1)y = ku
4		Колебательное	( T2p2+2ξTp+1)y = ku
5		Консервативное	(T2p2 + 1)y + ky
6	Ин- тегри- рую- щие	Идеальное интегрирующее
7		Интегрирующее с замедлением
8		Изодромное	py = (k+k1p)u
9	Диф- ферен- цирую- щие	Идеальное дифференцирующее	y = kpu
10		Дифференцирующее с замедлением	(Tp+1)y = kpu

Примечание: – постоянная времени, [с]; – коэффициент передачи звена; – коэффициент относительного демпфирования; – символ дифференцирования, равнозначный записи или ; – передаточный коэффициент.

Пример. Безынерционное (пропорциональное) звено

1. Дифференциальное уравнение: .

2. Конструктивное исполнение:

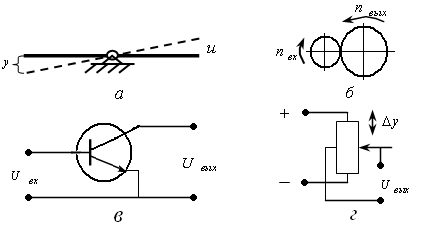
Рис. 9.13. - Примеры конструктивных исполнений:

а – рычаг; б – механический редуктор; в – транзистор; г – потенциометрический датчик, преобразующий механическое перемещение ползунка в электрическую величину , пропорциональную этому перемещению, т.е.

3. Временные характеристики:

4 . Частотные характеристики:

5. Логарифмические частотные характеристики:

Рис. 9.16. Логарифмические частотные характеристики

Примеры и характеристики остальных динамических звеньев приведены в приложении П. 1, а также в справочниках и учебниках.