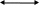1.3.2 Математические модели прохождения оптического излучения через биоткань

Принципы построения модели биологической ткани

При описании взаимодействия оптического излучения с биотканью, как правило, считается, что кожа представляет собой неоднородную непрозрачную мутную среду [9 – 17], следовательно, при взаимодействии излучения с веществом присутствует как поглощение, так и рассеяние.

В то же время, кожа является живой многослойной средой, содержащей различные включения, такие как, например, кровеносные сосуды, в которых происходит движение крови. Все это осложняет понимание процессов, происходящих при воздействии излучением на кожу. Для описания этих процессов на данный момент существует множество различных математических и физических моделей, каждая из которых призвана решить какую-либо конкретную задачу, описать частный случай.

Практически все модели строятся по одинаковым принципам. Сначала описывается объект исследования, его геометрия. Затем определяются оптические и физические параметры всех его компонентов. Далее производится расчет распространения излучения в среде, и (для некоторых моделей) вычисление температурных полей.

Различия между моделями становятся заметны уже на этапе построения геометрии биоткани. В большинстве случаев кожа представляется в виде последовательности плоских слоев с различными оптическими и теплофизическими свойствами. Количество слоев кожи может варьироваться от одного до семи. Самая простая геометрия включает в себя только дерму [15]. Такая упрощенная модель используется, например, для моделирования лечения угревой болезни лазерным излучением с длиной волны 1450 нм. В данной работе считалось, что поскольку на этой длине волны излучение поглощается преимущественно водой, то можно считать кожу одним цельным слоем с оптическими свойствами, близкими к свойствам воды.

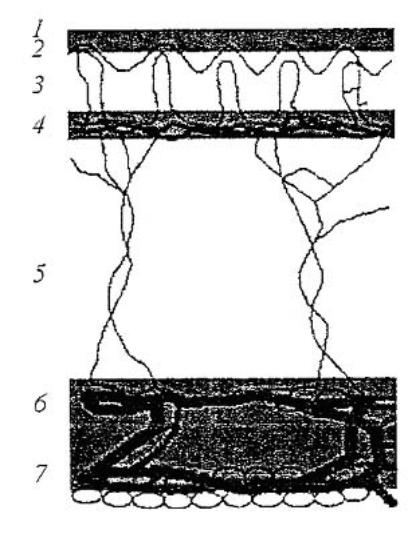
Наибольшее количество слоев модели представлено в работе [18]. В этой работе проводится анализ по методу Монте-Карло (MK) процессов распространения лазерного излучения в многослойных биоматериалах. В коже выделяются 7 слоев: роговой слой, эпидермис, верхняя дерма, дерма с поверхностным сплетением сосудов, нижняя дерма, дерма с глубинным сплетением сосудов, гиподерма (рисунок 42, a). Каждый из указанных слоев имеет свои оптические характеристики. Однако такое достаточно подробное разделение кожи на слои используется только для оптического расчета.

В некоторых работах, например в [18], наличие кровеносных сосудов в коже моделировалось с помощью изменения оптических свойств выделенных в дерме плоских слоев, в которых предполагается наличие крови.

а	б
Рисунок 42 - Модели кожи. Модель из семи слоев (а) [18]:1 – роговой слой, 2 – эпидермис, 3 – капиллярная (верхняя) дерма, 4 - верхнее сплетение микрососудов, 5 – ретикулярная (нижняя) дерма, 6 – глубокое сосудистое сплетение, 7 – гиподерма. Модель из трех слоев (б) [19]: I – эпидермис, II – дерма, III – гиподерма

Некоторые авторы выделяют кровь как отдельный слой с характеристиками чистой крови, либо как некий объект внутри ткани [14].

Кроме того, в работе [14] модель представляет собой структуру из трех слоев в упрощенном виде (рисунок 42, б): I – эпидермис, II – дерма, III – гиподерма. Обычно модель из трех слоев применяется для расчета распределения температуры [10 – 14, 17].

Сложное строение кожных покровов, имеющих разные оптические свойства, говорит о сложном механизме взаимодействия излучения с биологическими тканями, поэтому более точные оценки будут получены при использовании модели кожи из семи слоев. Надо сказать, что оптические параметры слоев ткани человека для разных длин волн информация весьма редкая, поэтому при отсутствии оптических параметров для всех семи слоев можно перейти к трехслойной модели.

Для построения модели необходимо рассмотреть взаимодействие излучения с биотканью, в результате можно определить, какие оптические параметры слоев необходимы. Существуют несколько видов взаимодействия излучений с биотканью [16, 20]: отражение, преломление, поглощение и рассеяние.

Отражение. Коэффициент отражения от кожи лежит в пределах от 10 до 55% (учитывается зеркальное и диффузное отражение) и зависит от спектра излучения, а также от степени пигментации и морщинистости кожи, наличия жира и влаги, которые, в свою очередь, зависят от пола, возраста и цвета кожи (расы). В инфракрасном диапазоне кожа может отражать до 40% излучения, имеются некоторые различия, связанные с полом и возрастом пациента, пигментацией его кожных покровов и др. [15]. Уменьшить отражение и, тем самым, повысить эффективность воздействия можно путем очистки зоны воздействия от жира и пота протиркой спиртом или эфиром, смазывания раствором йода или бриллиантовой зелени. Ещё одним методом является непосредственный контакт излучателя с кожным покровом и легким прижатием к телу, вызывающим местный отток крови и тем самым увеличение прозрачности ткани [15].

Поглощение. Вследствие поглощения интенсивность падающей электромагнитной волны ослабляется при прохождении через среду. Поглощение электромагнитного излучения существенно зависит от структуры биоткани. Экспериментальными работами показано [15], что для инфракрасного излучения в диапазоне 800 ÷ 1200 нм кожа поглощает 25 ÷ 30%.

Рассеяние. Помимо поглощения, кожа характеризуется значительным светорассеянием, т. е., как уже говорилось, является сильно рассеивающей мутной средой, т. к. состоит из большого числа случайно распределенных в объеме рассеивающих центров [15, 21 – 24]. Степень рассеяния зависит от длины волны излучения и оптических свойств биоткани. В оптимальной для фотоплетизмографии ближней инфракрасной области спектра 600 ÷ 1500 нм рассеяние превалирует над поглощением. Сильное рассеяние обусловлено соизмеримостью длины волны излучения с размерами клеток и отдельных их элементов (ядро, митохондрии, волокна цитоскелета и пр.). По мере того, как свет проникает через кожу, коллимированная структура пучка полностью заменяется на диффузную, обратное рассеяние возрастает и интенсивность отраженного от кожи света достигает 35 ÷ 70% от интенсивности падающего пучка [15].

Поглощение света биологическими тканями в красном и ближнем ИК-диапазоне обусловлено в основном кровью и водой, содержащейся в тканях. Возможность проведения фотоплетизмографических исследований обусловлена сильным рассеянием и отражением ИК излучения эритроцитами (большей частью их поверхности) [25, 26].

При описании взаимодействия света с биологическими тканями используют следующие оптические параметры [15]:

Основные:

μ_α – коэффициент поглощения среды, мм ^-1;

μ_s – коэффициент рассеяния среды, мм ^-1;

p(Θ) – угловая фазовая функция рассеяния.

Производные:

μ_t = (μ_α + μ_s) – общий коэффициент ослабления, мм ^-1;

l_ph=1/μ_t – средняя величина свободного пробега фотона, мм;

А = μ_s/μ_t – альбедо;

g – параметр анизотропии (по определению, фактор анизотропии g представляет собой средний косинус угла рассеяния и определяется экспериментально).

В случае если g = 1 рассеяние происходит только вперед, g = -1 – рассеяние только назад и если g = 0 – изотропное рассеяние.

В упрощенном виде модель взаимодействия оптического излучения с биотканью как с одним слоем представлена на рисунке (рисунок 43) [12, 20].

Падающий на биоткань световой поток Ф₀ частично отражается от ее поверхности, причем отраженный поток можно разделить на две составляющие: зеркальную и диффузную . Излучение, которое прошло внутрь ткани Ф_вн, частично поглощается и частично рассеивается в ней (поток Ф_рас). Рассеяние является причиной распространения значительной доли излучения в обратном направлении (обратное рассеяние) [12, 15, 20, 24].

Рисунок 43 - Схема взаимодействия оптического излучения с биологической тканью [12]

Часть рассеянного в обратном направлении излучения Ф_{обр. рас}, не поглощенного за время распространения в ткани, выходит из биоткани наружу со стороны падения излучения. И, наконец, оставшаяся часть излучения проходит через слой ткани и выходит с другой ее стороны, при этом могут формироваться два потока: прошедший без рассеяния прямой поток Ф_пр и диффузно рассеянный в прямом направлении поток Ф_{пр. рас}. Очевидно, что информативными потоками излучения являются Ф_{обр. рас} и Ф_{пр. рас}, Ф_пр в зависимости от типа используемого октрона.

Изображенный на рисунке 43 поток оптической помехи Ф_оп от посторонних источников света (фоновая, паразитная засветка) может действовать как непосредственно на фотоприемник, минуя биообъект, так и взаимодействовать, как и поток Ф₀, с биообъектом и, следовательно, складываться с полезными потоками Ф_{обр. рас} и Ф_{пр. рас}, Ф_пр.

Теперь, когда описано взаимодействие с одним слоем, можно перейти к более сложной модели биоткани, в которой необходимо учитывать взаимодействие излучения с несколькими слоями.

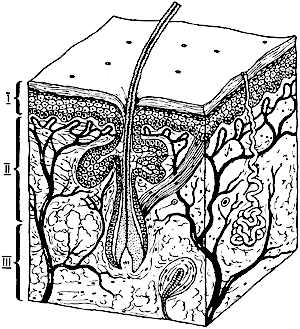
На рисунке 44 представлены 7 слоев, которые соответствуют семи слоям, изображенным на рисунке (42, а), с рассматриваемыми потоками.

Рисунок 44 - Упрощенная модель взаимодействия излучения со слоями биоткани: Ф0 – падающий на биоткань световой поток; Ф΄0 – световой поток, который не взаимодействовал с биотканью; Фотр – поток, отраженный от поверхности слоя первого слоя (роговой слой); Ф1..5,7 – поток рассеянного излучения, вышедший из биоткани, и связанный с взаимодействием светового потока со слоями с первого по пятый и седьмым слоем; Ф6 – поток рассеянного излучения, вышедший из биоткани, и связанный с взаимодействием светового потока со слоем 6 (глубокое сосудистое сплетение); Фпр – поток излучения, прошедший биоткань; 1 … 7 – слои соответствующие слоям биоткани; ФП – фотоприемник (гипотетическое местоположение)

Введя коэффициенты передачи светового потока k₁, ... k₇, указанные потоки можно выразить в следующем виде:

Ф_i=k_i ∙Ф₀

где k – коэффициент передачи, учитывающий процесс взаимодействия (поглощение, рассеяние и отражение) излучения с i-м слоем и всеми предыдущими,

i – индекс обозначающий номер слоя.

Отраженный от поверхности биоткани световой поток Ф_отр запишется в следующем виде:

Ф_отр=k_отр ∙Ф₀

где k_отр – коэффициент отражения поверхности биоткани (учитывает зеркальное и диффузное отражение).

Кроме того, нужно учесть тот факт, что не весь поток от излучателя Ф_изл взаимодействует с биообъектом. Часть этого потока, например, вследствие широкой диаграммы направленности, рассеяния в оптических компонентах оптической системы или бликов от элементов крепления может, в принципе, достичь фотоприемника минуя биоткань (поток Ф′₀). Поток прямой засветки Ф_{пр.засв} (та часть потока Ф′₀, которая достигает фотоприемника), можно представить в виде:

Ф_{пр.засв.}=k_{пр.засв.} ∙ Ф′₀

где k_{пр.засв} – коэффициент передачи излучения за счет прямой засветки от излучателя.

Таким образом, от биоткани идет суммарный световой поток Ф_Σ:

Ф_Σ = (Ф₁ + Ф₂ + … + Ф₇) + Ф_отр.

Из-за конечности размеров чувствительной площадки фотоприемника на нее падает только часть суммарного светового потока Ф_Σ и потока Ф_{пр.засв}. Поэтому, введя коэффициенты сбора световых потоков β_i, получим:

Ф_ФП = (β₁Ф₁ + β₂Ф₂ +…+ β₇Ф₇ )+ β_отрФ_отр + β_{пр.засв}Ф_{пр.засв}.

Коэффициенты сбора световых потоков зависят от размеров фоточувствительной площадки фотоприемника, апертуры и пропускания фокусирующей системы, углового распределения распространения световых потоков и др.

Поток излучения ИИ, падающий на биоткань Ф₀, является частью полного потока излучения ИИ. Введя коэффициент полезного использования потока ИИ γ_пол, можно записать:

Ф₀ = γ_пол ∙Ф_ИИ.

Поток Ф′₀ также можно охарактеризовать коэффициентом использования γ′:

Ф′₀ = γ′∙ Ф_ИИ.

Таким образом, для потока излучения, попадающего на фотоприемник Ф_ФП, получим:

Ф_ФП = Ф_ИИ ∙γ_пол∙ + γ_пол∙ β_отр ∙k_отр ∙Ф_ИИ + γ′∙β_{пр.засв} ∙k_{пр.засв}∙ ∙Ф_ИИ

В предположении монохроматичности излучения поток Ф_ИИ равен:

Ф_ИИ = (полное число испускаемых фотонов) ∙ (энергия фотона, Е_ф), т.е.

Ф_ИИ = I_И ∙η(I_И) ∙Е_ф

Ф_ФП = I_И ∙η(I_И) ∙K_ок ∙Е_ф.

Произведение I_И ∙η(I_И) – полное число фотонов, испускаемых источником излучения, а I_И ∙η(I_И) ∙K_ок – полное число фотонов, попавших на фотоприемник.

Изменение потока Ф₆ связанного с шестым слоем (глубокое сосудистое сплетение) будем считать изменением информативной составляющей всего потока, так как именно эта составляющая в большей степени связана с изменением содержания крови в участке биологической ткани.

Математическое описание распространения оптического излучения в мутных средах

Математическое описание характеристик поглощения и рассеяния света может быть проведено двумя способами – с помощью аналитической теории и с помощью теории переноса. Первая основывается на уравнениях Максвелла и в принципе является наиболее фундаментальным подходом. Однако её использование ограничено сложностью получения точных аналитических решений. С другой стороны, теория переноса в основном рассматривает перенос фотонов через поглощающие и рассеивающие среды, не основываясь на уравнениях Максвелла. Она имеет эвристический характер и ей не хватает строгости аналитических теорий. Тем не менее, теория переноса широко используется для описания взаимодействий лазерного излучения с тканью и экспериментально подтверждено, что во многих случаях ее прогнозы являются достаточными.

Теория переноса, называемая также теорией переноса излучения, берет свое начало с работы Шустера 1903 г. Теория оперирует непосредственно переносом энергии в среде, содержащей частицы. Сама по себе она не включает дифракционных эффектов. Предполагается, что при суммировании полей отсутствует корреляция между ними так, что складываются интенсивности, а не сами поля [15]. Уравнение переноса является интегро-дифференциальным уравнением лучевой интенсивности и общий его вид нас не интересует, однако, интерес представляет реализация уравнения переноса с помощью различных приближений. Главная проблема, с которой имеет дело теория переноса, – определение диффузной составляющей лучевой интенсивности, так как рассеяние фотонов носит случайный характер. Поэтому применяются различные приближения, в соответствии с которыми доминирующим процессом ослабления света является либо поглощение, либо рассеяние. Наиболее часто используемыми являются следующие методы:

• теория Кубелки-Мунка,

• диффузионное приближение,

• метод Монте-Карло.

Рассмотрим коротко эти приближения.

Теория Кубелки-Мунка. Теория Кубелки-Мунка – это частный случай так называемой многопотоковой теории, где уравнение переноса превращается в матричное дифференциальное уравнение, учитывающее лучевую интенсивность в направлении многих отдельных телесных углов. Однако данная теория имеет дело только с диффузной компонентой лучевой интенсивности и ограничена случаями, когда рассеяние во много раз превышает поглощение. Другим неудобством теории Кубелки-Мунка является то, что она может быть применена только для одномерной геометрии системы [15, 27].

Диффузное приближение. Данное приближение предполагает, что диффузная часть потока интенсивности встречает много частиц и рассеивается на них почти равномерно во всех направлениях, поэтому угловое распределение рассеянного потока почти изотропно. Но угловая зависимость не может сводиться к константе, так как поток при этом обращается в нуль и распространения мощности не будет. Поэтому диффузную компоненту потока интенсивности делают немного большей для направления полного потока, чем для обратного направления. Данное приближение достаточно трудоемкое и требует решениям множества уравнений для каждого слоя биоткани [15].

Метод Монте-Карло. Метод Монте-Карло – это численный метод решения математических задач (систем алгебраических, дифференциальных, интегральных уравнений) и прямое статистическое моделирование (физических, химических, биологических, экономических, социальных процессов) с помощью получения и преобразования случайных чисел.

Общая схема метода Монте-Карло основана на Центральной предельной теореме теории вероятности, утверждающей, что случайная величинa , равная сумме большого количества N произвольных случайных величин X_i с одинаковыми математическими ожиданиями m и дисперсиями σ², всегда распределена по нормальному закону с математическим ожиданием и дисперсией . [15].

С точки зрения решения уравнения переноса излучения, метод Монте-Карло заключается в компьютерном моделировании случайного блуждания N числа фотонов. Для получения приемлемой аппроксимации необходимо рассматривать большое количество фотонов, поскольку точность результатов, пропорциональна N.

Главной идеей метода является учет явлений поглощения и рассеяния на всем оптическом пути фотона через непрозрачную среду. Расстояние между двумя столкновениями выбирается из логарифмического распределения, используя случайное число, генерируемое компьютером. Для учета поглощения вводится случайное число между 0 и 1. Если это число менее , то происходит рассеяние, в противном случае происходит поглощение. Если имеет место рассеяние, выбирается новое направление распространения в соответствии с фазовой функцией и другим случайным числом. Эта процедура продолжается до тех пор, пока фотон не выйдет из рассматриваемого объема или не поглотится.

Метод Монте-Карло включает в себя пять основных шагов: генерация источника фотона, генерация траектории, поглощение, ликвидация, регистрация. После накопления достаточного количества фотонов, карта траекторий рассчитывается и накапливается в компьютере. Таким образом, может быть получен статистический отчет о порции падающих фотонов, поглощенных средой, а также пространственное и угловое распределение фотонов, вышедших из нее. Реализации данного метода рассмотрены в работах [10 – 18, 23, 28]. В основном все работы направлены на рассмотрение тепловых процессов, возникающих при распространении излучения в веществе.

В работе [15] результаты по взаимодействию излучения с биологической тканью были получены с помощью метода Монте-Карло, теории Кубелки-Мунка, диффузионного приближения и аналитического решения уравнения переноса излучения, которое возможно, поскольку рассматривается случай изотропного рассеяния. Отмечено, что результаты, полученные с помощью диффузионного приближения, практически всегда совпадают с результатами, полученными методом Монте-Карло и достаточно близки с аналитическим решением уравнения переноса, в то время как результаты, полученными с помощью теории Кубелки-Мунка значительно отличаются от аналитического решения.

Кроме решений уравнения переноса различными приближениями, моделирование распространения оптического излучения в многослойных мутных средах возможно с использованием искусственных нейронных сетей (ИНС). ИНС включает в себя сеть так называемых искусственных нейронов, связанных между собой синаптическими соединениями (синапс – место контакта между двумя нейронами или между нейроном и получающей сигнал эффекторной клеткой. Главная задача искусственного нейрона заключа­ется в умении формировать правильный выходной сигнал в зависимости от сигналов, поступающих на его входы. Преобразуя входной сигнал во времени, ИНС меняет свое внутреннее состояние и формирует искомые выходные параметры. Большинство ИНС требуют процесса многомерной оптимизации параметров («обучения сети»), для реализации которого существуют различные алгоритмы. Для осуществления моделирования с использованием нейронных сетей необходимо большое количество информации, полученной в результате проведения экспериментов, только в этом случае возможно обучение сети и получения правильного выходного сигнала [29, 32].

Таким образом, наиболее подходящим методом для моделирования прохождения излучения через многослойную биоткань, в нашем случае, можно считать численный метод Монте-Карло.

Математическое моделирование взаимодействия оптического излучения с биологической тканью с помощью метода Монте-Карло пакете MathCAD 13

На основе представлений о решении уравнения переноса методом Монте-Карло разработаем базовый алгоритм, учитывающий специфику фотоплетизмографических исследований с использованием планарного датчика.

Будем рассматривать биоткань, как случайно-неоднородную рассеивающую и поглощающую среду, а распространяющуюся в нем энергию как поток энергии, т.е. все эффекты, связанные с волновой природой света (дифракция, интерференция, поляризация), не принимаем во внимание. Основным преимуществом данного метода является моделирование достаточно сложной геометрии и неоднородностей среды [12]. Показатели преломления отдельных слоев и связанные с ними явления при моделировании учитываться не будут, однако реализация закона преломления на границе воздух-биоткань осуществлена.

Моделируемая среда задается следующими параметрами для каждого слоя: толщиной слоя h_si, коэффициентами рассеяния µ_si и поглощения µ_ai, средним косинусом угла рассеяния g_i. Среда представляется совокупностью центров, рассеивающих и поглощающих фотоны [15].

Проследим в деталях алгоритм распространения пакета фотонов (рисунок 15). Падающий поток излучения состоит из заданного числа фотонов, входящих в среду вдоль оси y перпендикулярно ее поверхности (либо под углом γ) (y=0). Координата x для каждого из фотонов выбирается случайным образом из значений равномерно распределенных в интервале ( , ), где d_is – диаметр источника, координата у для каждого фотона равна 0.

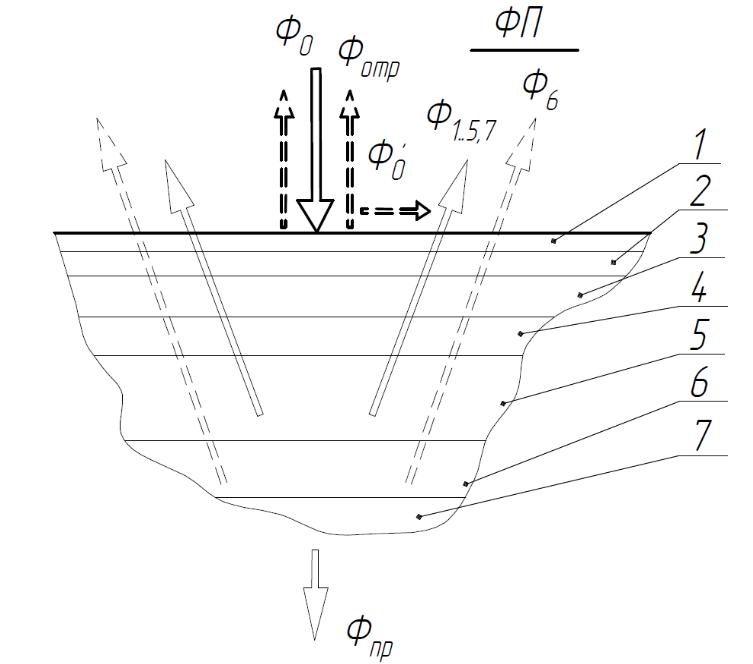
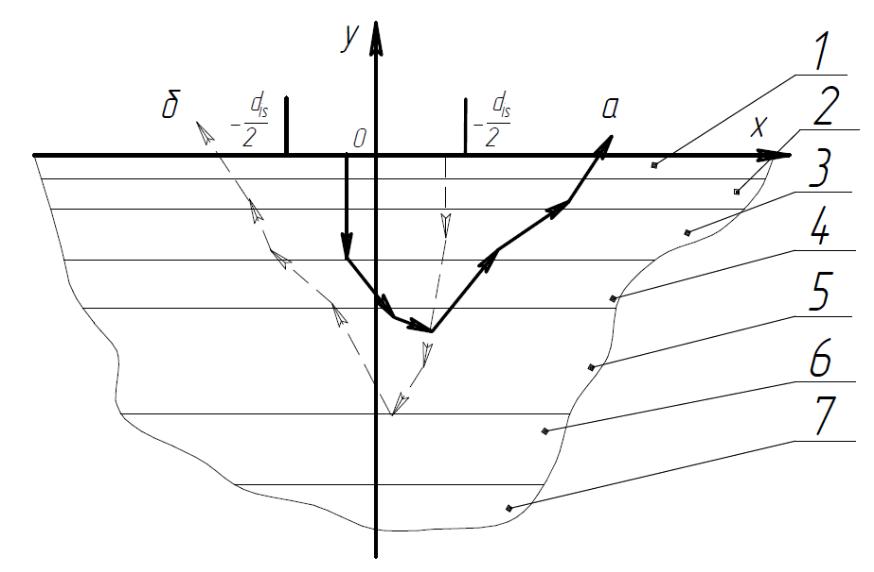
Все расчеты производятся в двухмерной декартовой системе координат, т.е. считаем, что все фотоны распространяются в одной плоскости (рисунок 45). После входа фотона в образец определяются длина свободного пробега (l_d) фотона в среде и угол рассеяния θ.

Предполагаем, что частицы среды, на которых происходит рассеяние и поглощение, являются сферически симметричными. Такое приближение часто используется в аналогичных случаях и основано на том, что в процессе прохождения через среду с сильным рассеянием фотон взаимодействует с частицами под разными углами. Поэтому можно применять усредненную индикатрису рассеяния. Использование данной модели и сравнение численных расчетов с экспериментальными результатами показали, что данное приближение удовлетворительно описывает свойства большинства биологических тканей [10 – 17, 23, 28].

Рисунок 45 - Пояснения к алгоритму: 1 – первый слой; 2 – второй слой; dis – диаметр источника; θ – угол рассеяния; hs1 – толщина первого слоя; ld – длина свободного пробега; γ – угол входа фотона в биоткань; a – фотон

В случае ткани с сильным рассеянием в качестве фазовой функции рассеяния можно применить фазовую функцию Хени-Гринштейна. Из функции Хени-Гринштейна [12, 15] получают выражение для угла θ:

где ξ₁ – случайное число из диапазона равномерно распределенных чисел (0; 1), которое выдается генератором случайных чисел (ГСЧ), в дальнейшем все случайные величины будут выбираться тем же образом;

g – параметр анизотропии (средний косинус угла рассеяния).

На каждом шаге угол θ определяется относительно «старого» направления распространения. Обычно данную задачу решают в трехмерных декартовых координатах. При этом кроме угла рассеяния θ вводят угол φ, который откладывается в плоскости перпендикулярной направлению распространения фотона. Он принимает значение от 0 до 2π . Так как мы решаем двухмерную задачу, то введем случайное число из диапазона (0; 1) – ξ₂. Если ξ₂ принадлежит области (0; 0.5), то угол θ_f (угол распространения в первоначальных координатах) будет определяться как

где θ_{f 0} – предыдущий угол распространения фотона.

Если ξ₂ принимает значение из области [0.5; 1), то θ_f будет определяться как

Длина свободного пробега фотона определяется выражением [10]:

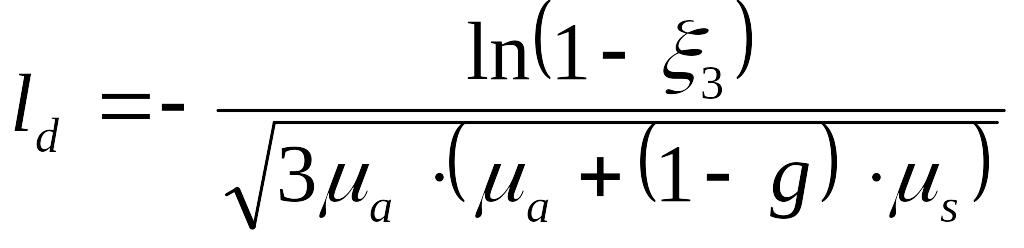
Число ξ₃, определяется случайным образом из интервала (0; 1). Значения коэффициентов рассеяния µ_s и поглощения µ_a определяются в зависимости от координаты рассеяния фотона.

После этого моделируется взаимодействие фотона с частицей среды, которая может быть либо поглощающим, либо рассеивающим центром. Вероятность рассеяния фотона на частице определяется как [10, 15]:

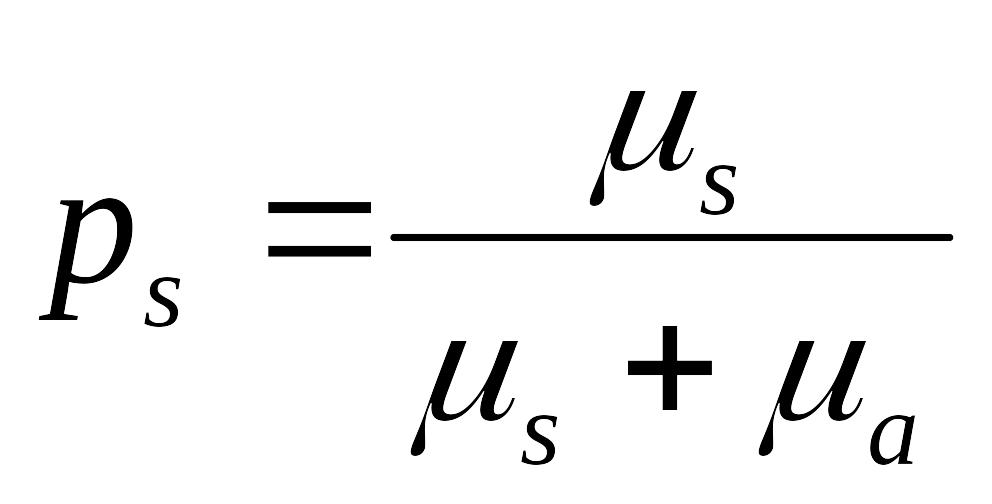
При этом задается число ξ₄, также определяемое случайным образом из интервала (0; 1). Если ГСЧ выдает случайное число в диапазоне (0; p_s), то считается, что фотон рассеян, в противном случае – поглощен.

Весь слой среды вдоль оси y виртуально поделен на некоторое количество более тонких слоев с толщиной h_si и параметрами (µ_si, µ_аi, g_i), которые соответствуют усредненным параметрам слоев биологической ткани, представленной на рисунке (12, а).

Если фотон рассеян, то рассчитываются его новое направление движения и координаты по формулам:

Если фотон достиг границы со слоем 6 (глубокое сосудистое сплетение), то моделируется обратное рассеяние на эритроцитах [25] в виде отражения от границы между пятым и шестым слоем, при этом координата соприкосновения с шестым слоем ( ,H₆) определяется как [32]:

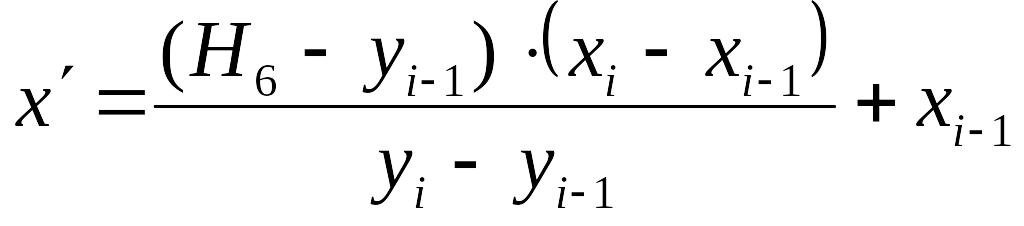
где H₆ – это координата y границы между пятым и шестым слоем;

(x_i-1, y_i-1) –старые координаты фотона;

(x_i, y_i) - новые координаты фотона.

Под коэффициентом обратного рассеяния R_e будем понимать вероятность того, что фотон, достигнув границы со слоем 6, отразится. Некоторые авторы моделируют этот процесс поглощением крови рассеянного излучения, идущего с более глубоких слоев [15]. В любом случае, по мере усложнения модели можно перейти от бесконечно тонкого слоя к непосредственному взаимодействию с глубинным сплетением сосудов и гиподермой.

Для моделирования обратного рассеяния от эритроцитов введем число ξ₅, выбираемое случайным образом из интервала (0; 1). Если ξ₅ находится в диапазоне (0; R_e), то происходит обратное рассеяние (факт рассеяния регистрируется), если нет, то регистрируется, что фотон прошёл (он нас больше не интересует), и переходим к следующему фотону.

Если фотон рассеялся в обратном направлении на эритроците, то его угол отражения равен углу падения, при этом длина свободного пробега берется как расстояние между точками (x_i, y_i) и ( ,H₆) [32]:

Далее, если фотон в результате многократного рассеяния достиг границы с воздухом, то рассчитывается координата выхода фотона ( ,0) по формуле [32]:

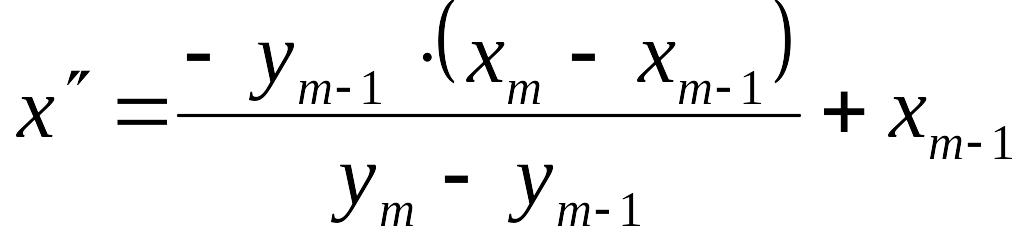
где (x_m-1, y_m-1) – старые координаты фотона;

(x_m, y_m) – новые координаты фотона.

Рисунок 46 - Иллюстрация многократного рассеяния фотонов в биоткани: (а) – неинформативный фотон; (б) – информативный фотон; 1 … 7 – слои соответствующие слоям биоткани

Данные обо всех фотонах и их траекториях анализируются, фотоны достигшие границы с воздухом делятся на информативные (рисунок 16, фотон «б»), т.е. которые провзаимодействовали с эритроцитами (гемоглобином), и неинформативные (рисунок 46, фотон «а»), которые не взаимодействовали с эритроцитами.

Основной задачей процесса моделирования является выбор наиболее адекватной к оригиналу модели и перенос результатов исследования на эксперимент.

При построении модели были введены следующие упрощения:

1. кожа представляется в виде последовательности плоских слоев с различными оптическими свойствами;

2. толщина и оптические свойства каждого слоя усредненные;

3. распространяющуюся в биоткани энергию представляем как поток энергии, т.е. все эффекты, связанные с волновой природой света (дифракция, интерференция, поляризация), не принимаем во внимание;

4. работа в одной плоскости;

5. предполагаем, что частицы среды, на которых происходит рассеяние и поглощение, являются сферически симметричными;

6. не учитываем изменение показателя преломления слоев;

7. не учитываем долю отраженной от биоткани энергии на границе воздух-биокань;

8. полное внутренне отражение на границе биоткань-воздух так же не учитываем;

9. при взаимодействии с частицей считаем, что фотон либо рассеется, либо поглотится;

10. не учитываем изменение геометрии пятна при изменении угла наклона источника.

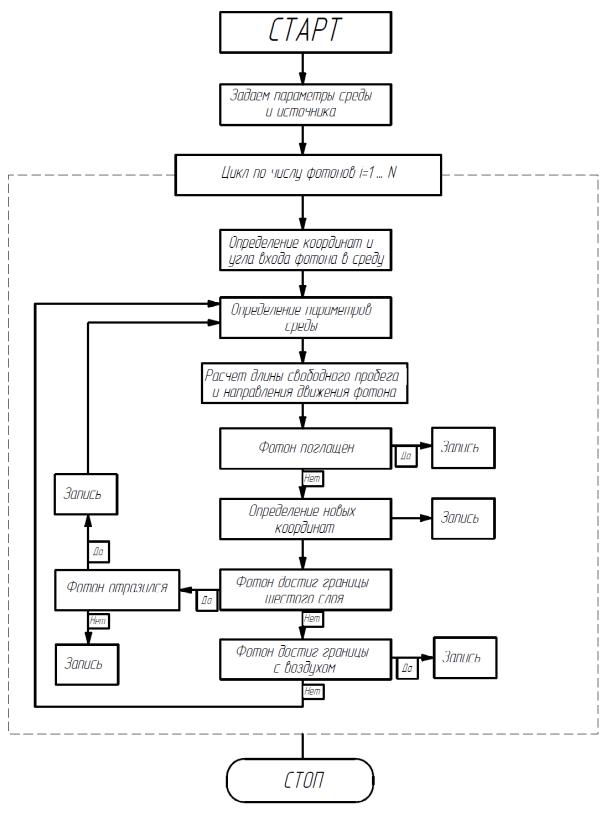
Схема алгоритма представлена на рисунке 47.

Рисунок 47 - Схема алгоритма метода Монте-Карло применительно к методу отражательной фотоплетизмографии

Распределение рассеянных фотонов в зависимости от диаметра источника (падение нормальное)

Моделирование взаимодействия излучения с биологической тканью проводилось для двух длин волн 633 нм и 810 нм. Оптические параметры неоднородной среды для длины волны 633 нм представлены в таблице 4. Оптические параметры среды для длины волны 810 нм представлены в таблице 5.

Предполагаем, что все фотоны попадают в биоткань, т.к. отраженный от поверхности биоткани поток не представляет интереса. Фотоны по диаметру пучка распределены равномерно. Вероятность обратного рассеяния фотонов на эритроцитах возьмем 20% (R_e=0.2).

Таблица 4 – Оптические свойства слоев кожи, используемые при моделировании (λ=633 нм) [9, 17]

Слой	µs (мм-1)	µa (мм-1)	g	Толщина (мм)
Роговой слой	100	0.8	0.9	0.02
Эпидермис	60	0.15	0.85	0.08
Дерма с капиллярными петлями	30	0.07	0.9	0.15
Дерма с поверхностным сплетением сосудов	35	0.1	0.95	0.08
Дерма	25	0.05	0.76	1.5
Дерма с глубоким сплетением сосудов	35	0.15	0.95	0.08

Таблица 5 – Оптические свойства слоев кожи, используемые при моделировании (λ=810 нм) [33,34]

Слой	µs (мм-1)	µa (мм-1)	g	Толщина (мм)
Эпидермис	11.5	0.205	0.8	0.1
Дерма	5	0.024	0.8	1.81
Кровь	30	0.068	0.995

Вид функции распределения неинформативных фотонов от расстояния для двух длин волн в результате моделирования получается похожими (рисунок 48).

Рисунок 48 - Рассеянный поток для длин волн 633 нм и 810 нм. (N=1000000, dis=3 мм, Re=0.2)

Уровень неинформативного потока (количество фотонов) для λ=633 нм при одних и тех же условиях в 2 раза выше неинформативного потока для λ=810.

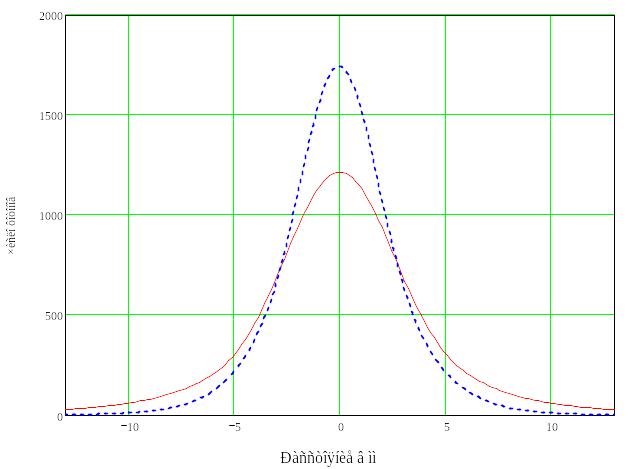
Рисунок 49 иллюстрируют функцию распределения фотонов взаимодействующих с эритроцитами (информативный поток) и функцию распределения фотонов невзаимодействующих с эритроцитами (неинформативный поток) для длины волны 633 нм. Результаты расчета показали, что при условии: N=1000000, d_is=3 мм, R_e=0.2 и λ=633 нм: уровень информативного потока составлял 34% от полного рассеянного в обратном направлении потока.

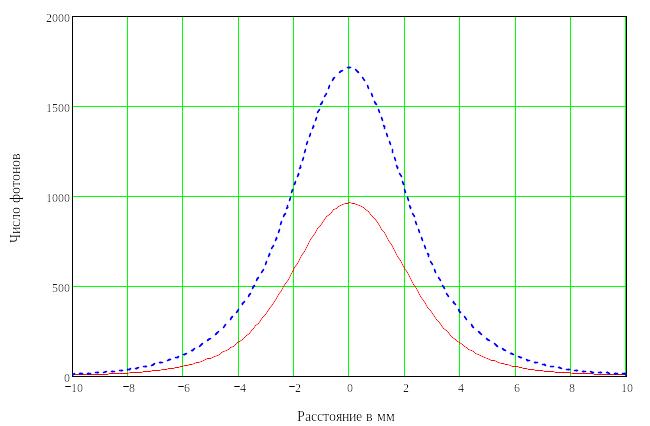
Информативный поток в случае с длиной волны 810 нм оказался больше, при этом неинформативный поток стал меньше (рисунок 50). Уровень информативного потока при λ=810 нм составлял 62% от полного рассеянного в обратном направлении потока.

dis

Рисунок 49 - Рассеянные потоки. (N=1000000, dis=3 мм, Re=0.2, λ=633 нм)

dis

Рисунок 50 - Рассеянные потоки. (N=1000000, dis=3 мм, Re=0.2, λ=810 нм)

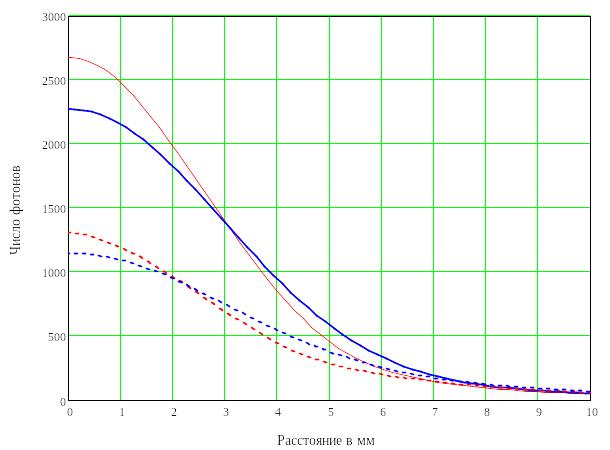
Изменение распределения информативного и неинформативного потоков при изменении диаметра источника представлено на графиках рисунков 51 и 52 для λ=633 нм и λ=810 нм соответственно.

Так как функция симметричная, то на графиках можно ограничиться только частью функции для первой четверти декартовой системы координат. Это позволяет продемонстрировать различия в функции при смене диаметра источника излучения.

2.5 0.5

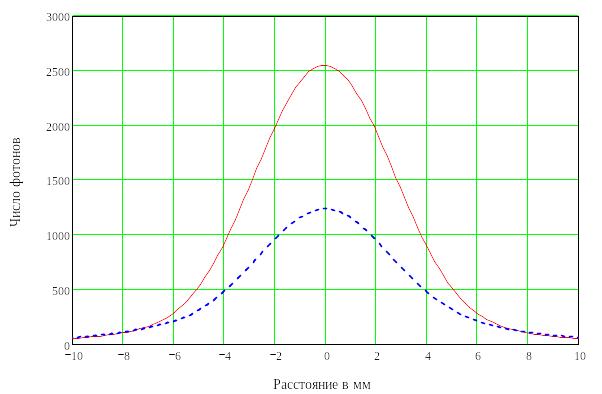
Рисунок 51 - Вид функций распределения фотонов для информативной (сплошная линия) и для неинформативной (прерывистая линия) составляющей рассеянного потока фотонов. (N=1000000, Re=0.2, λ=633 нм)

С точки зрения построения датчика для ФПГ, изменение сигнала в центре функции, говорит о том, что при большом диаметре источника значительная часть потока возвращается в область под источником излучения, и не может быть зарегистрирована. Данные моделирования для λ=810 нм показали, что при d_is=1 мм в область под источником попадает около 24% от информативного потока, а при d_is=5 мм – 69% .

2.5 0.5

Рисунок 52 - Вид функций распределения для информативной (сплошная линия) и для неинформативной (прерывистая линия) составляющей рассеянного потока фотонов. (N=1000000, Re=0.2, λ=810 нм)

Согласно полученным результатам получается, что если падение излучения нормально, то приемник должен быть как можно ближе к источнику. С точки зрения размеров источников, применение источника с меньшим диаметром является более предпочтительным.

Вид функции распределения рассеянных фотонов в зависимости от угла входа излучения в биоткань (диаметр источника постоянный)

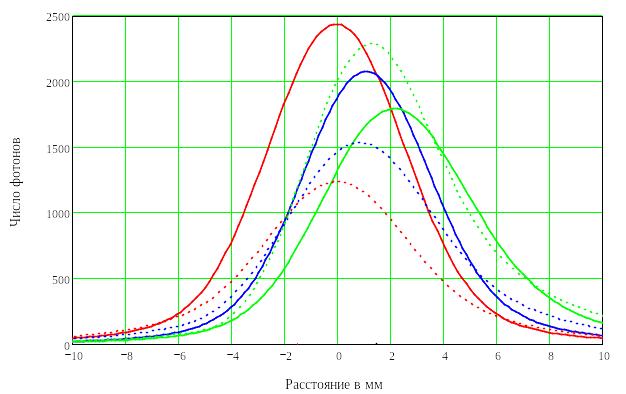
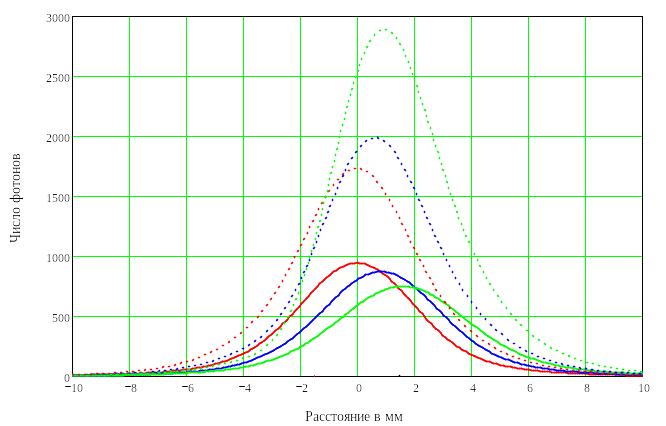
Так как биологическая ткань – слоистая структура с изменяющимися оптическими параметрами, то возможно ожидать, что наклон источника излучения и/или приемника на оптимальный угол приведет к увеличению информативного сигнала при определенном расстоянии между источником и приемником. На рисунке 53 для длины волны 810 нм и рисунке 54 для длины волны 633 нм представлено изменение уровня информативного сигнала и местоположения его максимума для трех углов наклона. При моделировании диаметр источника оставался постоянным и составлял 3 мм, количество фотонов в импульсе составляло 1000000. В качестве примера углы наклона составляли 90° (нормальное падение), 110° и 130°. Результаты изменения информативной и неинформативной частей потока при изменении угла наклона источника от 90° до 150° представлены в таблице 6.

dis

Рисунок 53 - Функции распределения информативного (сплошная линия) и неинформативного (прерывистая линия) потока фотонов для различных углов наклона источника излучения. (N=1000000, dis=3 мм, Re=0.2, λ=810 нм)

Таблица 6 – Потоки при различных углах наклона источника излучения (λ=810 нм, N=100000)

Угол наклона источника, °		Количество неинформативных фотонов	Количество информативных фотонов	Общее число рассеянных фотонов	Отношение количества информативных фононов к общему, %
90		6443	10792	17235	63
95		6433	10766	17199	63
100		6643	10750	17393	62
105		7067	10649	17716	60
110		7549	10297	17846	58
115		8222	10194	18416	55
120		9078	10076	19154	53
125		10107	9826	19933	49
130		11591	9514	21105	45
135		13290	9036	22326	40
140		15319	8455	23774	36
145		18066	7981	26047	31
150		20952	7396	28348	26
	x1 x2
	Рисунок 54 - Функции распределения информативного (сплошная линия) и неинформативного (прерывистая линия) потока фотонов для различных углов наклона источника излучения. (N=1000000, dis=3 мм, Re=0.2, λ=633 нм)

Если сравнивать координаты максимума функции распределения информативного и неинформативного потока при одном и том же значение угла наклона источника, то видно, что максимум неинформативного сигнала находится ближе к началу координат, чем максимум сигнала от глубокого сосудистого сплетения (рисунок 54).

Результаты, полученные при моделировании для длины волны излучения 633 нм (рисунок 54), аналогичны результатам для длины волны 810 нм, при этом информативная составляющая рассеянного излучения для длины волны 633 нм меньше той же составляющей для длины волны 810 нм.

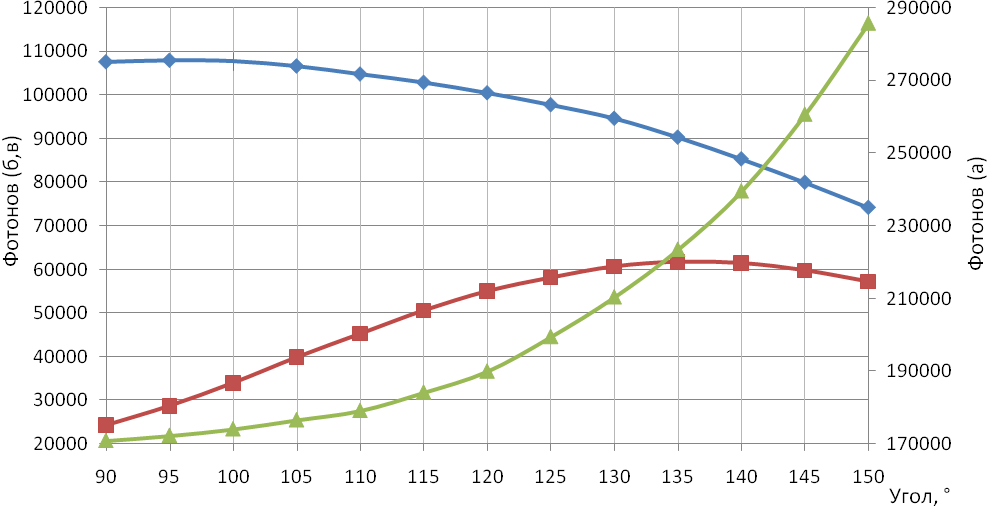
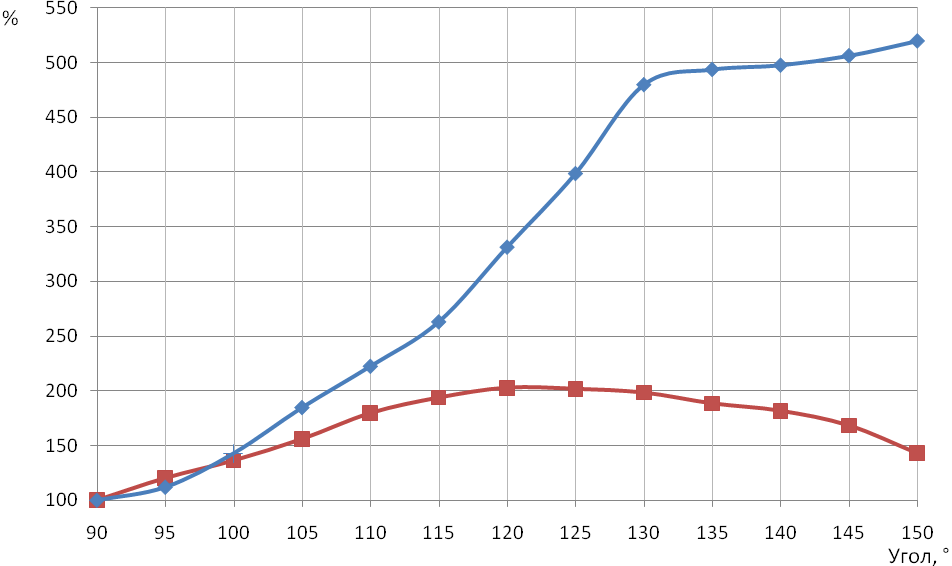
При увеличении угла наклона, количество фотонов рассеянных в обратном направлении увеличивается (рисунок 55, a), при этом количество информативных фотонов уменьшается (рисунок 55, б). За счет увеличения угла наклона источника функция распределения информативных фотонов смещается вправо, как было показано на рисунке 53 и 54. Это приводит к тому, что количество фотонов справа от источника увеличивается (рисунок 25, в). Рост числа информативных фотонов справа от источника наблюдается до 135° затем идет спад.

Рисунок 55 - Зависимости: (а) – общего числа фотонов рассеянных в обратном направлении от угла наклона источника; (б) – количества информативных фотонов от угла наклона источника, (в) – количества фотонов справа от источника. (N=1000000, dis=3 мм, Re=0.2, λ=810 нм)

Так как при получении пульсовой кривой регистрируется изменение потока, попадающего на фотоприемник за счет изменения кровенаполнения ткани, то в модели будем описывать это явление положительным изменением коэффициента рассеяния ΔR_e. Изменение коэффициента рассеяния будет влиять на приращение числа фотонов в рассеянном информативном потоке. Проанализируем как меняется сигнал в области детектирования размером 3 мм при расстоянии между областью детектирования и источником, например, 3 мм и 6 мм, изменение коэффициента рассеяния 10% (таблица 7) (рисунок 56).

Таблица 7 – Результаты моделирования (λ=810 нм, изменение коэффициента отражения 10%, N=1000000)

Угол наклона приемника в градусах	Абсолютное изменение числа фотонов при расстоянии между источником и приемником:		Относительное увеличение сигнала при расстоянии между источником и приемником 3 мм и 6 мм. (90° как базовый 100%), %
	3 мм	6 мм	3 мм	6 мм
90	10042	1580	100	100
95	12076	1769	120	112
100	13690	2258	136	143
105	15655	2918	156	185
110	18032	3513	180	222
115	19453	4154	194	263
120	20362	5232	203	331
125	20251	6294	202	398
130	19911	7576	198	479
135	18922	7796	188	493
140	18245	7857	182	497
145	16897	7994	168	506
150	14354	8207	143	519

На графике (рисунок 56 для 6 мм) видно, что с увеличением угла наклона можно добиться значительного увеличения уровня сигнала, стоит отметить, что картина будет меняться при изменении расстояния между источником и приемником. Так, если область детектирования непосредственно вблизи источника (рисунок 26 для 3 мм), то при изменении угла наклона наблюдается рост числа фотонов, а затем спад числа фотонов, связанный с уменьшением общего числа информативных фотонов.

Рисунок 56 - График относительного увеличения числа фотонов зарегистрированных в области детектирования размером 3 мм. Расстояния между источником и приемником 3 мм и 6 мм. (N=1000000, dis=3 мм, λ=810 нм)

Оптимальный угол для наклона приемника в существующей модели выделить не представляется возможным, так как в результате многократного рассеяния распределение углов выхода фотонов с изменение угла наклона источника не претерпевает особых изменений. Наиболее оптимальным с точки зрения этой модели, считается расположение фотоприемника, так чтобы его оптическая ось совпадала с нормалью к поверхности биоткани. Изменение угла наклона источника приводит как к увеличению полезного сигнала, так и к увеличению неинформативного сигнала. Выбор оптимального угла для любого источника и приемника возможен лишь при решении задачи на оптимизацию, т.е. при которой отношение сигнал/шум будет максимальным.

Модель прохождения излучения через биоткань (геометрическое приближение – диффузное отражение от границ раздела слоев)

Существует две разновидности фотоплетизмографических методов: фотоплетизмография в отраженном, точнее рассеянном в обратном направлении свете и фотоплетизмография в проходящем свете. При исследовании биотканей в проходящем свете с использованием трансмиссионных датчиков осуществляется прямая оценка кровенаполнения в изучаемом участке биологического объекта. Однако при этом довольно сложно проводить исследования для оптически малопрозрачных биологических объектов. К тому же количество участков для установки трансмиссионных датчиков на теле биообъекта ограничено. В то же время метод фотоплетизмографии в отраженном свете с применением планарных датчиков более универсален, и позволяет исследовать кровенаполнение на плоских участках тела.

В настоящее время электронная часть аппаратуры для фотоплетизмографии разработана на достаточно высоком техническом уровне в отличие от фотоплетизмографических датчиков. Это обусловлено многими причинами: ограниченной номенклатурой фотоприемников, сложным, с точки зрения оптики, процессом взаимодействия оптического излучения с биологической тканью, особенно при разработке планарных оптоэлектронных датчиков.

В связи с этим, важным фактором повышения качества регистрируемых пульсовых кривых, а значит и достоверности получаемой диагностической информации, является совершенствование планарных оптоэлектронных датчиков.

Цель данной части работы: на основе анализа математической модели взаимодействия оптического излучения при диффузно направленном отражении дать рекомендации по конструированию планарных оптоэлектронных датчиков, используемых в фотоплетизмографии.

Для разработки оптоэлектронных датчиков, работающих «на отражение»/«обратное рассеяние» необходимо знать как геометрические параметры строения биологической ткани: толщина того или иного слоя ткани, глубина залегания (расположения) кровеносных сосудов – артерий и артериол, в которых и происходит изменение оптических свойств в результате изменения кровенаполнения, размеры сосудов и других поглощающих и рассеивающих свет образований и неоднородностей, так и оптические (спектральные) свойства этих объектов: коэффициенты поглощения, ослабления, рассеяния света, показатели преломления света и др. Эти данные, приводимые в литературе, достаточно противоречивы, что объясняется сложностью объекта исследования, а также отсутствием единства методик по измерению этих параметров.

Для моделирования распространения оптического излучения в рассеивающих биологических средах предложен ряд моделей [28, 34 – 37]. В данной работе используется упрощенная схема строения биологической ткани и упрощенный механизм взаимодействия излучения с биотканью [38]. Суть упрощения состоит в том, что кожная ткань представляется в виде слоистой структуры, в которой выделены наиболее характерные слои кожи в «чистом» виде. Модель распространения света в биоткани при диффузно направленном отражении представлена на рисунке 57.

Кожная ткань представляется в виде слоистой структуры, состоящей из эпидермиса, дермы, крови и гиподермы. Слои параллельно залегают на различной глубине, каждый слой однороден по составу и свойствам. Каждый из выделенных слоев имеет свои характеристики: толщина, коэффициенты пропускания, поглощения, рассеяния и т.д. «Луч» света (в данном случае рассматривается именно абстрактный луч, имеющий бесконечно малые поперечные размеры) с длиной волны λ падает на границу раздела слоев воздух – эпидермис под углом α₀ (показатель преломления света в воздухе принят равным единице). На границе раздела воздух – эпидермис происходит отражение – преломление света, прошедший через слой эпидермиса, а «луч» света испытывает диффузно-направленное отражение на границе раздела эпидермис – дерма (имеется в виду, что отражение - рассеяние света на границе раздела не является чисто ламбертовым, а есть угол «блеска»). Этот же механизм отражения – рассеяния приписывается и всем остальным границам раздела слоев.

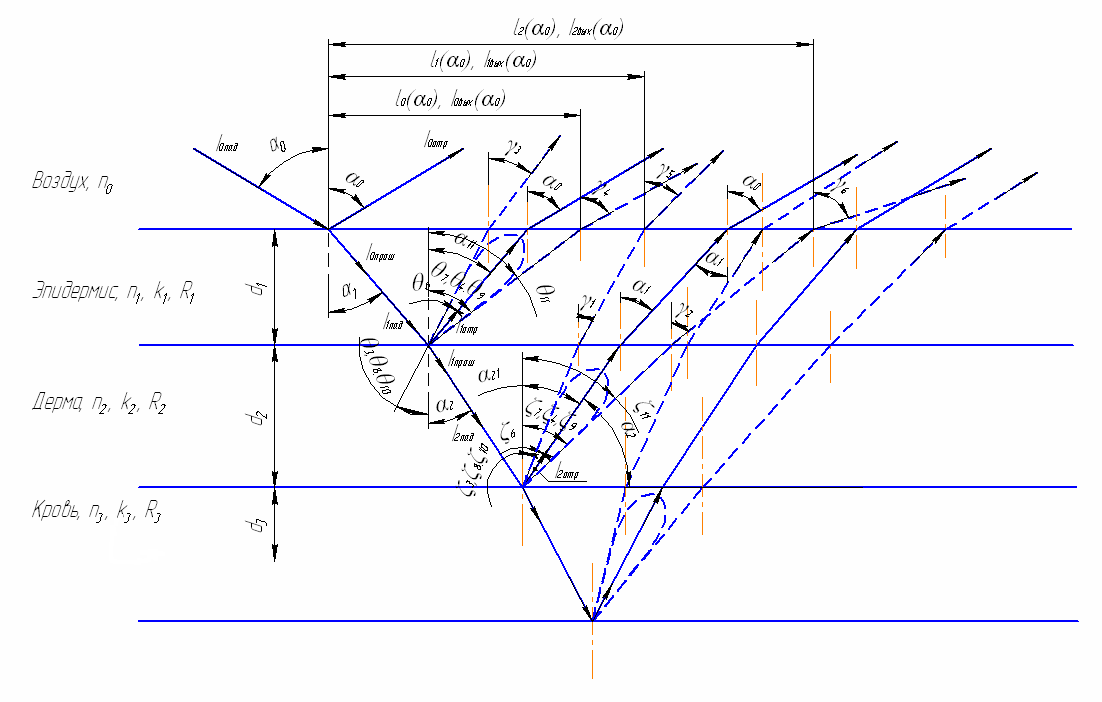
Рисунок 57 – Распространение света при диффузно направленном отражении

Процесс взаимодействия оптического излучения со слоем дерма и кровь аналогичен вышеописанному взаимодействию оптического излучения со слоем эпидермиса. Регистрация осуществляется диффузно отраженного излучения от границы раздела слоев эпидермис – дерма, дерма – кровь и кровь – гиподерма (рисунок 57). Лучи света, несущие полезную информацию об изменении свойств крови (кровенаполнения слоя «кровь») – это лучи, прошедшие через слой кровь, а также отразившиеся от границ раздела слоев дерма – кровь и кровь – гиподерма. Полезная информация связана с изменением как коэффициентов отражения границы раздела дерма – кровь, так и с изменением поглощения и рассеяния слоя кровь (последний процесс не учитывается в данной работе).

Распределение интенсивности оптического излучения при диффузном отражении описывается по закону косинуса, тогда

, где

– интенсивность диффузно направленного отраженного луча;

– интенсивность луча падающего на i^-ый слой биоткани;

– параметр диффузного угла отражения, влияющий на форму косинусного распределения;

– угол блеска;

– фазовый сдвиг.

Исходя из определения косинуса для первой четверти декартовой системы координат, можно найти асимптотические углы, ограничивающие угол диффузно направленного отражения (угол блеска).

Угол диффузно направленного отражения i-го слоя зависит только от угла падения света на биоткань и показателей преломления нулевого и рассматриваемых слоев биоткани.

Согласно закону Снелиуса можно найти углы преломления оптического излучения при прохождении света через границы раздела слоев биоткани и выхода излучения из биоткани в воздух.

Зависимость расстояния выхода излучения из биоткани от точки ввода, диффузно отраженного границами раздела слоев кровь – гиподерма, дерма – кровь, эпидермис – дерма от угла ввода излучения в биоткань приведена на рисунке 2 (дерма – кровь, кровь – гиподерма нижняя и верхняя асимптоты и эпидермис – дерма – нижняя асимптота).

В соответствии с рисунком 58 оптимальным диапазоном углов ввода излучения в биоткань является угол ввода излучения, начиная с 27°, при котором можно «собрать» полезную информацию на расстоянии от 0,07 мм от точки ввода излучения в биоткань. На рисунке 58 это область расстояний, лежащих выше кривой эпидермис – нижняя асимптота и между кривыми кровь – нижняя асимптота и дерма – верхняя асимптота.

Но введение оптического излучения в «точку» для биоткани может привести, во-первых, к увеличению влияния артефактов [39], связанных с состоянием поверхности биоткани (пигментация, загрязнения, волосяной покров и др.), особенно при исследовании животных: аномальный участок кожи может практически полностью перекрыть поток излучения и существенно уменьшить сигнал с датчика, а значит и отношение сигнал/шум, во-вторых, к перегреву биоткани и, в-третьих, к непредсказуемым результатам измерения и нежелательным последствиям при попадании излучения в зону биологически активной точки. Поэтому необходимо рассмотреть случай точечного источника, расположенного на некотором расстоянии от биоткани, дающего световой поток с конечной расходимостью.

Исходя из зависимостей, приведенных на рисунке 58, можно определить координаты выхода излучения из биоткани, диффузно отраженного от слоев дерма и кровь, при разных углах падения на биоткань и при разных расстояниях от источника излучения до биоткани. Это позволяет определить диапазон расстояний выхода излучения информативного и неинформативного сигналов (рисунок 59).

Информативный сигнал изображен на рисунке 59 сплошной линией. Это то самое расстояние, которое задает габариты фотоприемника. Минимальный угол подбирается таким образом, чтобы координаты выхода излучения из слоя эпидермис не пересекались с координатой выхода излучения, отраженного от слоя дерма. При этом условии отсекается неинформативный сигнал, снижающий качество регистрируемых фотоплетизмограмм. При смещении луча происходит потеря части информативного сигнала, что при соответствующей конструкции датчика можно избежать, введя дополнительные оптические элементы в конструкцию.

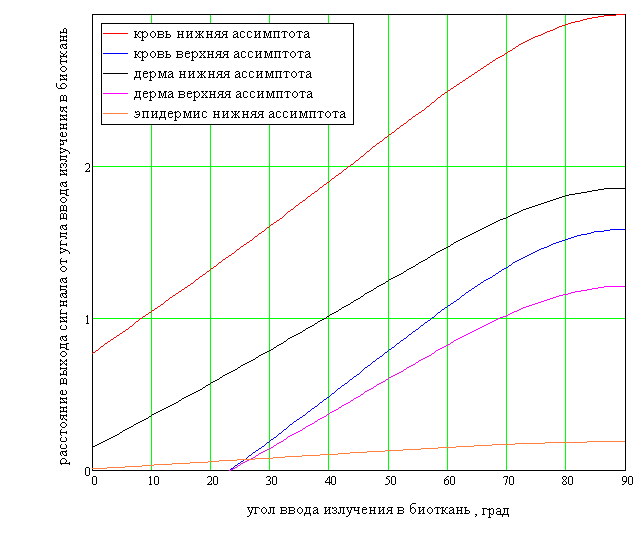
Рисунок 58 – Зависимость расстояний выхода излучения из биоткани, диффузно отраженного от границ раздела слоев кровь – гиподерма, дерма – кровь, эпидермис – дерма от угла ввода излучения в биоткань

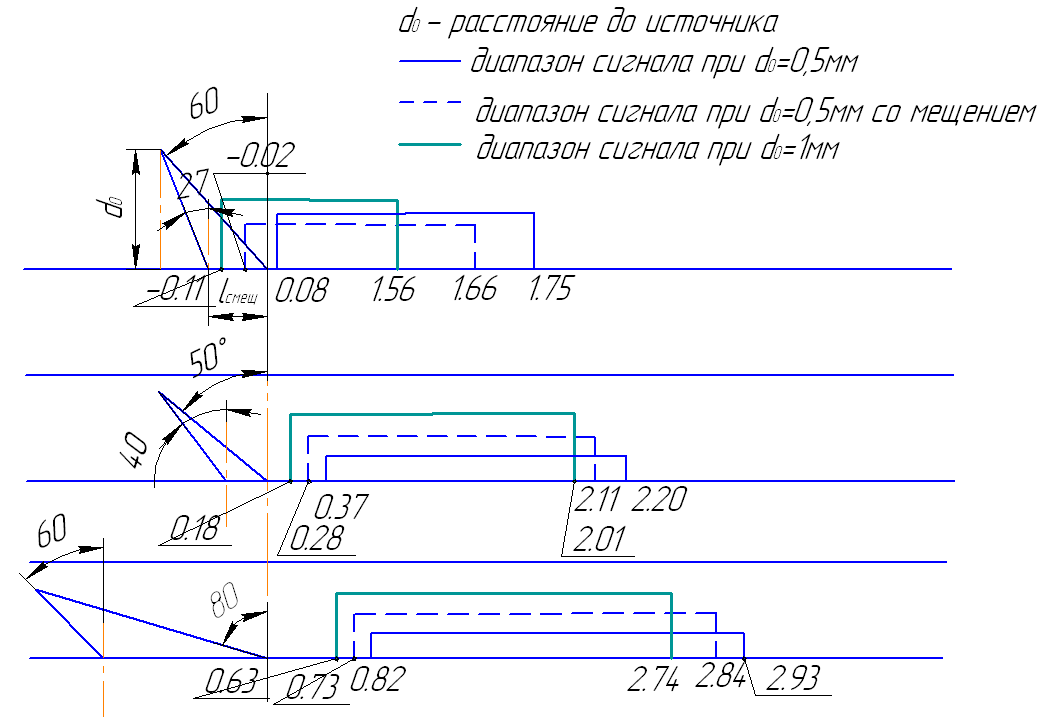
Рисунок 59 – Диапазон расстояний выхода излучения из биоткани диффузно отраженного от слоев дерма и кровь при точечном источнике с конечной расходимостью при разных углах падения света на биоткань. Глубина залегания слоя «кровь» - 0,8 мм

Проведенные расчеты позволяют выбрать конструктивные параметры планарного оптоэлектронного датчика для фотоплетизмографии с учетом конкретного участка биоткани. К ним относятся расстояние между источником и приемником излучения, его диаграмма направленности (угол наклона излучателя относительно поверхности биоткани и расходимость излучения), высота расположения излучающего элемента над поверхностью биоткани. Полученные результаты позволят повысить качество регистрируемых фотоплетизмограмм, а значит и уровень диагностики состояния сердечно-сосудистой системы человека и животных.