1.3 Математические модели прохождения оптического излучения через биоткань и водную среду

1.3.1 Математические модели для описания прохождения оптического излучения через водную среду с примесью

Во многих жидкостях, анализ которых представляет интерес, содержатся как растворенные вещества, так и взвешенные частицы различного происхождения (твердые или коллоидные). Для исследования таких систем часто применяют методы, основанные на рассеянии света. Распределение частиц по размерам находят, исследуя индикатрису рассеяния при фиксированной длине волны и решая затем соответствующую обратную задачу. Дополнительный вклад в погрешность измерения индикатрисы рассеяния вносит поглощение света, это накладывает существенные ограничения на выбор длины волны, особенно при анализе окрашенных жидкостей. Для определения концентрации взвешенных частиц используют методы, основанные на измерении экстинкции. При прохождении света через окрашенную жидкость экстинкция обусловлена как поглощением (абсорбцией), так и рассеянием. При измерении оптической плотности такой жидкости на спектрофотометре или фотоколориметре разделить вклады этих составляющих достаточно сложно.

Существует математическая модель, использующая уравнения теории Ми и приближение однократного рассеяния [8]. Это приближение справедливо либо при малой концентрации рассеивающих частиц, либо в слоях малой толщины. Форма частиц предполагается сферической. Из теории Ми следует, что интенсивность рассеяния I в прозрачной среде при неполяризованном падающем излучении определяется формулой

где S₁ и S₂ — амплитудные функции рассеяния, соответствующие поляризации рассеянного излучения в плоскости рассеяния и в перпендикулярной к ней плоскости. Для сферической частицы радиуса a

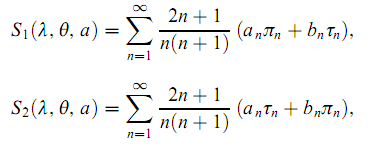
где а_п и b_n — коэффициенты Ми, а π_n и τ_n — угловые коэффициенты рассеяния. Коэффициенты Ми выражаются через a, λ и относительный показатель преломления т = n_par/n_liq (n_par и n_liq — показатели преломления рассеивающей частицы и жидкости соответственно, модель учитывает их зависимость от длины волны), а угловые коэффициенты рассеяния определяются углом Θ и вычисляются с помощью рекуррентных формул. Показатели преломления n_par и n_liq в общем случае считаются комплексными, их мнимая часть позволяет учесть поглощение света и его зависимость от длины волны.

Для рассеяния в поглощающей среде следует учитывать поглощение как падающего, так и рассеянного излучения. Для малоуглового рассеяния, возбуждаемого параллельным пучком интенсивность рассеяния , где Т — коэффициент пропускания среды.

Для системы, состоящей из N рассеивающих частиц, неупорядоченно распределенных в пространстве, результирующая интенсивность поля является суммой интенсивностей полей, рассеянных отдельными частицами. Необходимо также учесть поглощение как падающего, так и рассеянного излучения средой и взвешенными в ней частицами. Если рассеивающие частицы находятся в кювете с длиной оптического пути l и просвечиваются параллельным световым пучком, то для интенсивности рассеяния под малыми углами в (cosΘ~1) можно записать

Здесь с — массовая концентрация взвешенных частиц, к_т. — линейный показатель поглощения среды, k_sus. — массовый показатель поглощения взвешенной частицы,

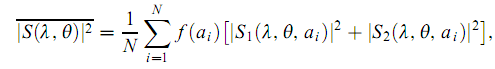
N — общее число взвешенных частиц, a_i — радиус i-й частицы, f(a_i) — функция распределения частиц по радиусам.

В программной среде MathCAD была написана программа по расчету диаграммы рассеяния на сферической частице, используя теорию рассеяния Ми. Диаграмма рассеяния строилась в зависимости от размера рассеивающей частицы. Представим некоторые результаты в виде графиков в полярной системе координат (рисунки 37-41).

Рисунок 37- Диаграмма рассеяния частицей размером λ/20

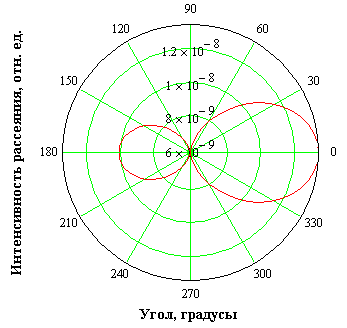
Рисунок 38- Диаграмма рассеяния частицей размером λ/10

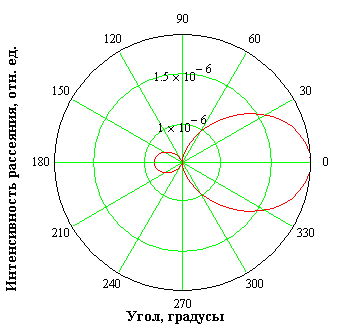
Рисунок 39- Диаграмма рассеяния частицей размером λ/5

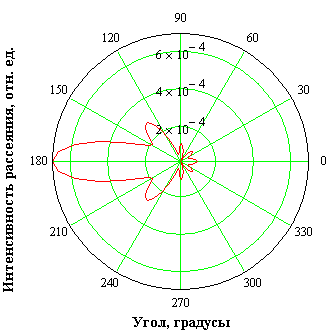
Рисунок 40- Диаграмма рассеяния частицей размером λ

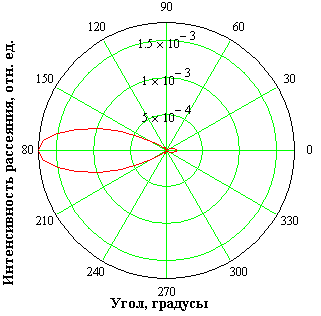
Рисунок 41- Диаграмма рассеяния частицей размером 5λ

Полученные диаграммы позволяют оценить долю излучения, рассеянную под определенным углом, выявить соотношения между рассеянными вперед и назад излучениями. Для размера частиц более длины волны имеет место малоугловое рассеяние; большая часть излучения рассеивается назад.

Рассчитаны доли полного рассеянного излучения одной частицей и доли рассеянного назад излучения. Результаты расчета программы сведены в таблицу 3:

Таблица 3 - Данные по расчету рассеянного излучения

Размер частицы, λ	Доля рассеянного излучения одной частицей.	Доля рассеянного излучения в назад 0,02 %-ого	Количество частиц в исследуемом объеме
1/20	0,341∙10-18	7,1∙10-10	1,13∙1012
1/10	1,62∙10-15	3,5∙10-7	1,42∙1011
1/5	23,17∙10-12	3,9∙10-4	1,77∙1010
1	0,946∙10-9	0,51	1,42∙108
5	4,82∙10-6	0,0213	1,13∙106
10	5,146∙10-6	2,83∙10-3	1,42∙105
50	55,59∙10-9	1,511∙10-8	1,13∙103

Зная количество рассеянного излучения, рассчитывается концентрация примеси в исследуемой среде по следующей формуле (предполагается, что интенсивность излучения рассеянного единицей объема в заданном направлении в N раз больше интенсивности, рассеянной одной частицей; N – количество частиц):

где D – диаметр пучка, проходящего прозрачную среду;

F_рас - интенсивность рассеянного излучения;

F₀ – интенсивность рассеянного излучения одной частицей;

l – длина оптического пути;

C – концентрация взвешенных частиц.

Разработанная математическая модель позволяет определить, насколько ослабевает излучение, проходящее прозрачную среду, в результате процесса рассеяния, и рассчитать концентрацию взвешенных в среде веществ зная долю рассеянного излучения. Из расчета доли рассеянного излучения для N частиц в облучаемом объеме среды существенный вклад в ослабевание излучения за счет рассеяния вносят частицы размером λ,5λ и 10λ.