2.8. Равномерное распределение

Непрерывная СВ Х называется распределённой по равномерному закону c параметрами ( ), если множество её возможных значений – отрезок , а вероятность попадания СВ Х на любой участок этого отрезка пропорциональна длине участка. Плотность и функция распределения равномерно распределённой СВ имеют вид:

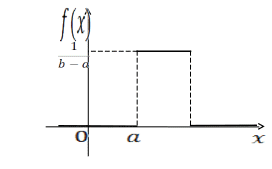
Для равномерного распределения , .

2.9. Показательное распределение

Непрерывная СВ Х называется распределённой по показательному (экспоненциальному) закону c параметром , если множество её возможных значений – полупрямая , а плотность и функция распределения имеют вид:

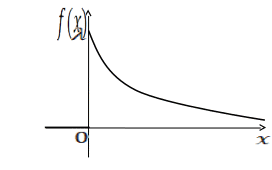
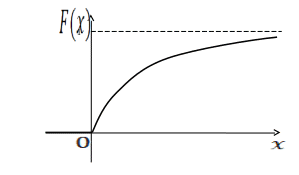
Для показательного распределения , .

2.10. Нормальное распределение

Непрерывная СВ Х называется распределённой по нормальному закону (по закону Гаусса) с параметрами и , если множество её возможных значений – вся числовая прямая, а плотность вероятности определяется формулой

.

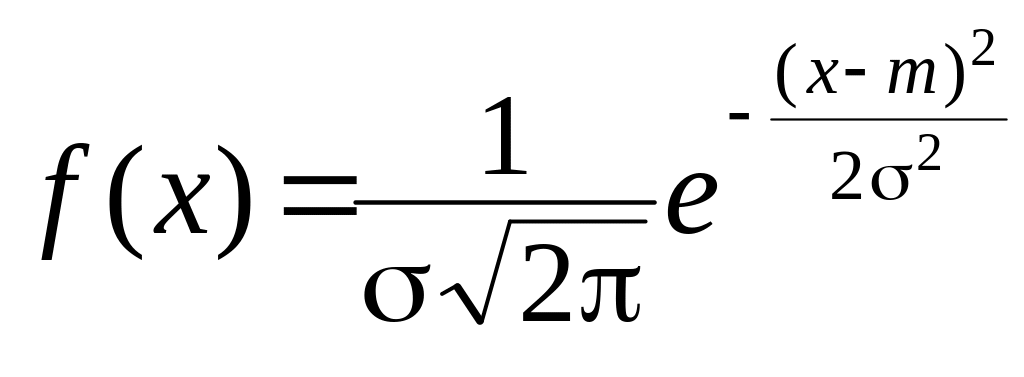Для нормального закона используется обозначение , при этом , , а функция распределения задаётся формулой

,

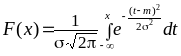где интеграл не выражается через элементарные функции. Графики плотности и функции распределения имеют вид:

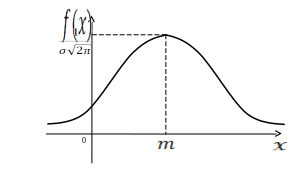
Нормальный закон распределения называется стандартным, если и . Для стандартного нормального закона плотность вероятности имеет вид и обладает свойством , а функция распределения имеет вид и обладает свойством . Функции и называются, соответственно, функцией Гаусса и функцией Лапласа. Для нахождения их значений при различных х составлены таблицы.

Если в выражении для функции распределения СВ сделать замену , то получим . При имеем , а при имеем . Отсюда

,

т.е. функция распределения нормального закона с заданными параметрами m и  выражается через функцию распределения стандартного нормального закона.

Поскольку для непрерывной СВ , то для нормально распределённой СВ . В частности,

.

Это означает, что попадание нормально распределённой СВ Х на отрезок – практически достоверное событие. Данное свойство нормального распределения называется “правилом трёх сигма”.

3. Случайные векторы

3.1. Понятие случайного вектора. Матрица распределения двумерного дискретного случайного вектора

На практике часто встречаются задачи, в которых результат опыта описывается не одним, а двумя или более числовыми значениями, заранее неизвестными. Примеры: точка попадания в мишень при выстреле характеризуется полярными координатами или декартовыми координатами ; осколок, образовавшийся при разрыве снаряда, характеризуется весом, размером, начальной скоростью и т.д.; результаты последовательных измерений меняющейся величины выражаются n числами. Подобные примеры приводят к понятию случайного вектора.оро0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

Случайным вектором (или системой случайных величин) называется упорядоченный набор случайных величин . Случайный вектор называется дискретным (непрерывным), если соответствующие СВ являются дискретными (непрерывными). Свойства случайного вектора не ограничиваются свойствами отдельных величин: они включают также взаимные связи (зависимости) между СВ.

Рассмотрим дискретный случайный вектор . Пусть и – упорядоченные по возрастанию возможные значения СВ Х и Y соответственно, а , , . Поскольку события , , попарно несовместны и образуют полную группу, то . Тогда под матрицей распределения вектора понимается следующая таблица:

Y	Х
			...
			...
			...
...	...	...	...	...
			...

Вероятности отдельных значений СВ Х и Y определяются равенствами:

и .

Отсюда видно, что зная матрицу распределения дискретного случайного вектора , можно найти ряд распределения каждой из СВ Х и Y.