Практична робота №1

Тема: Аналіз та оцінка фінансових інвестицій

Мета: закріплення теоретичних знань та набуття практичних навичок з розрахунку показників прибутковості акцій, обігу акцій; обчислення номінальної ціни та курсу акцій; визначення доцільності інвестицій

Вид заняття: практична робота

Методи проведення: пояснення, бесіда, самостійна робота студента.

Матеріально-технічне, інформаційне та дидактичне забезпечення: калькулятори, робочий зошит студента, завдання практичної роботи

Рекомендована література:

1. Інвестування: Навч.-метод.посібник для самост.вивч.дисц./А.А. Пересада та ін.-К.: КНЕУ, 2001.-251 с.

2. Майорова Т.В. Інвестиційна діяльність. Навч.пос.-К.: ЦУЛ,2003.-376 с.

3. Федоренко В.Г., Гойко А.Ф. Інвестознавство: Підручник.-К.: МАУП, 2000.-408 с.

Основні теоретично-розрахункові положення теми:

Акції можуть мати: номінальну, емісійну, балансову, конверсійну, ліквідаційну вартість і ринкову ціну або курс.

Номінальна вартість (номінал акції) — ціна, вказана на бланку акції. Вона характеризує частку статутного капіталу, яка припадає на одну акцію під час заснування компанії.

Емісійна вартість — ціна, за якою акція реалізується (продається) на первинному ринку; може відрізнятися від номіналу.

Балансова вартість — величина власного капіталу, що припадає на одну акцію. Якщо емітовано лише прості акції, то така вартість визначається діленням власного капіталу на кількість акцій. Якщо випущено й привілейовані акції, то власний капітал зменшується на сукупну вартість привілейованих акцій за номіналом або за викупною ціною (для відзивних акцій).

Ринкова вартість (або курсова вартість) — ціна, за якою акції продаються та купуються на ринку; саме за цією ціною акції котируються на вторинному ринку цінних паперів.

Курс акції — відношення ринкової ціни до номіналу, виражене у процентах.

Ліквідаційна вартість — визначається в момент ліквідації акціонерного товариства. Вона показує, якою є вартість майна акціонерного товариства, що припадає на одну акцію і підлягає реалізації у фактичних цінах після розрахунку з кредиторами.

За умови постійних виплат дивідендів поточна ринкова вартість простих акцій визначається як і з привілейованих акцій, тобто:

де P_a — поточна ринкова вартість акцій;

D — річна сума дивідендів;

r — норма дохідності акцій подібного класу ризику (десятковий дріб).

Приклад 1

Компанія сплачує річні дивіденди в розмірі 17 грн. на акцію, норма поточної дохідності за акціями даного типу становить 14 %. Яка має бути вартість акції?

Розв'язок

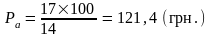
Відповідь:вартість акції має становити 121, 4 грн.

Для розрахунку поточної вартості акцій з постійним приростом дивідендів використовується так звана «модель Гордона»:

де g — річний темп приросту дивідендів, (десятковий дріб);g = const.

D₀ — дивіденди, сплачені компанією протягом року.

Ця формула g < r.

Приклад 2

Компанія протягом року виплатила дивіденди в розмірі 15 грн. на акцію. Щорічно дивідендні виплати зростають на 12,6 %, норма поточної дохідності за акціями даного типу становить 14 %. Яка має бути вартість акції?

Розв'язок

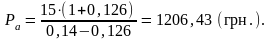
Відповідь: вартість акції становитиме 1206,43 грн.

У разі змінного темпу приросту дивідендів (g ≠ const) поточна вартість акцій розраховується за формулою:

де D_i — обсяг дивідендів, які інвестор прогнозує отримати в i-му періоді.

Приклад 3

Підприємство виплатило за останній рік дивіденди в розмірі 0,24 грн. на акцію. Протягом другого року воно збільшило дивіденди до0,2472 грн., третього — до 0,2645, у подальшому планується постійне зростання дивідендів на 8 % річних. Необхідно оцінити вартість акції за умови, що норма дохідності акцій даного типу становить 12 %.

Розв'язок

У даній задачі підприємство точніше визначає дивідендні виплати за перші три роки та здійснює прогноз постійного приросту дивідендів у безмежному періоді часу з урахуванням g (річного темпу приросту дивідендів). У подальшому оцінка поточної ринкової вартості акцій визначається дисконтуванням спрогнозованої сукупності дивідендів. Формула оцінки вартості акцій може мати такий вигляд:

У наступні роки підприємство планує щорічне збільшення дивідендів на 8 %, тому для визначення вартості акції використаємо формулу моделі Гордона:

Оскільки показник Р₂ дає оцінку вартості акції на кінець третього періоду, а необхідно знайти поточну вартість на початок першого періоду, здійснюється дисконтування:

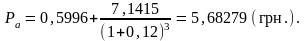
Відповідь: ціна акції складе 5, 68 грн.

Інвестори не завжди мають в своєму портфелі постійні обсяги і види певних фінансових інструментів; під впливом цілей інвестування відбувається зміна цінних паперів. Коли інвестор заздалегідь прогнозує термін використання певних акцій, їх поточна ринкова вартість може бути оцінена за формулою

де D_t — обсяг дивідендів, які інвестор прогнозує отримати у t-му періоді;

P_r — прогнозна вартість реалізації акцій в кінці періоду її використання;

n — кількість періодів використання акції.

Для аналізу ефективності операцій з акціями використовуються такі показники:

1. Ставка дивіденду (Д_д) визначається за формулою

де D — очікувані річні дивіденди, грн.;

N — номінальна вартість, грн.

2. Поточна ринкова дохідність (Д_р) визначається співвідношенням обсягів річних дивідендів і поточної ринкової вартості акції:

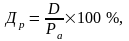
де Р_а — поточна ринкова вартість акцій, грн.

3. Поточна дохідність акцій для інвестора (Д_п) — рендит розраховується як співвідношення обсягу річних дивідендів і вартості придбання акції:

У разі прийняття рішення про доцільність придбання акції на основі рівня поточної дохідності інвестор, як правило, прогнозує довгострокові інвестиції в цей фінансовий актив. Тому сукупна дохідність у цьому разі, збігається з поточною дивідендною дохідністю.

За купівлі акцій з метою перепродажу через деякий час ураховуються дивідендна і капіталізована дохідність. Отже, сукупна (повна) дохідність може бути визначена за формулою

де D_i — річні дивіденди, які виплачуються в і-му році;

P_t — ринкова вартість акцій у t-му році;

P₀ — вартість придбання акцій.

Середньорічна сукупна дохідність (кінцева дохідність) за акціями визначається за формулою

Приклад 5

Інвестор придбав акцію номіналом 30 грн. за курсом 117 % і продав її через 4 роки за курсом 136 %. У перший рік рівень дивідендів становив 2,4 грн. на акцію, у другий рік ставка дивіденду становила 10 %, у третій — 11 %, у четвертий рік рівень дивідендів становив 3,4 грн. Розрахуйте сукупну дохідність і середньоріч­ну (кінцеву) дохідність акції.

Розв'язок

Дивіденди становили:

1 рік: 2,4 грн.;

2 рік: 30 грн. × 0,1 = 3 грн.;

3 рік: 30 грн. × 0,11 = 3,3 грн.;

4 рік: 3,4 грн.;

Вартість придбання акцій: Р₀ = 30 × 1,17 = 35,1 (грн.);

Ринкова вартість (продажу) Р_t = 30 × 1,36 = 40,8 (грн.).

Розраховуємо сукупну дохідність:

Визначення кінцевої дохідності:

Відповідь: сукупна дохідність акцій становить 50,71%, а середньорічна — 12,68%

Середньорічна сукупна дохідність (кінцева) за короткостроковими операціями може бути розрахована за формулою

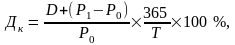
де Р₁ — вартість акції на момент продажу;

Т — кількість днів володіння акцією.

Приклад 6

Інвестор придбав акції ВАТ «Шелл» 18 вересня 2009 р. за ціною 25,6 грн., продав їх 25 березня 2010 р. за ціною 27,2 грн.; 15 лютого він отримав дивіденди в розмірі 1,6 грн. на акцію. Визначте середньорічну (сукупну) дохідність акції.

Розв'язок

Період володіння акціями (Т) = 12 + 31 + 30 + 31 + 31 + 28 + + 25 = 188 (дн.).

Відповідь: середньорічна дохідність акцій за короткостроковими операціями становить 24,27%.

Визначення майбутньої вартості поточної суми грошей (коумпандування):

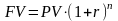, де

FV — майбутня вартість грошей або сума грошей на рахунку через n часових періодів;

PV — поточна вартість грошей або початкова сума грошей на рахунку;

r — ставка процента (десятковий дріб);

n — кількість часових періодів.

Приклад 7

Інвестор поклав у банк 1000 грн. під 24% річних із щоквартальним нарахуванням відсотків. Визначити величину суми вкладу через 2 роки.

Розв'язок

Щоквартальна ставка процента становитиме: . Крім того, щоквартальні нарахування відсотків означає збільшення кількості періодів (п) з 2 до 2 ∙ 4 = 8. Тепер розраховуємо майбутню суму на рахунку:

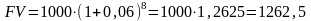(грн.)

Відповідь: через 2 роки вклад зросте до 1262,5 грн.

Процес визначення поточної вартості майбутньої суми грошей, тобто грошей, які мають надійти в майбутньому, називається дисконтуванням:

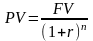
Крім номінальної ставки відсотка за депозит (і) у фінансових розрахунках використовується і ефективна ставка (EAR), або дійсна ставка відсотка, яка визначає відносний дохід, що одержує власник капіталу за рік в цілому при т нарахувань.

Приклад 8

Банк пропонує 2 варіанти нарахування відсотків по депозитам: Варіант І — нарахування здійснюються щоквартально за ставкою 26%. Варіант В — щомісячно за ставкою 27%. Визначити привабливіший варіант вкладу.

Розв'язок

Привабливішим буде той варіант вкладення коштів, при якому ефективна ставка відсотків буде більшою. Отже, знаходимо дійсні ставки відсотків по варіантам:

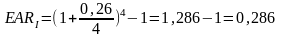(28,6%)

(26,8%)

Відповідь: І варіант розміщення коштів є привабливішим для вкладника.

Вибір варіанта завдання практичної роботи:

Номер варіанта	Номер студента у журналі
1	1,11,21
2	2,12,22
3	3,13,23
4	4,14,24
5	5,15,25
6	6,16,26
7	7,17,27
8	8,18,28
9	9,19,29
10	10,20,30