Допущения и ограничения.

1. Процесс стационарный.

2. Параметры сосредоточенные.

3. Угол трубопроводов к горизонту равен нулю. Нет потерь засчет разности уровней – поверхность идеальная.

4. Жидкость идеальная (несжимаемая и имеет постоянную плотность).

Потери давления на участке трубопровода:

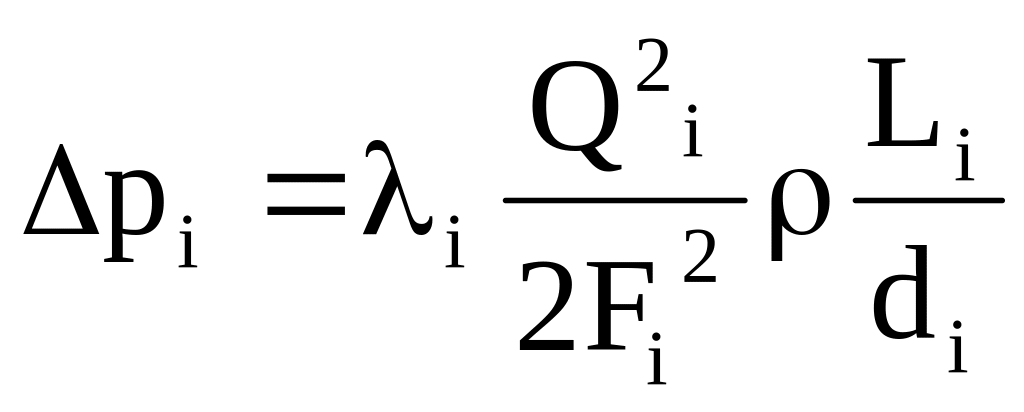(1)

Где:

- объемный расход

- площадь поперечного сечения

- диаметр трубопровода

- длина участка

- плотность жидкости

- коэффициент гидравлического сопротивления

Массовый расход определяется формулой: , тогда перепишем уравнение (1):

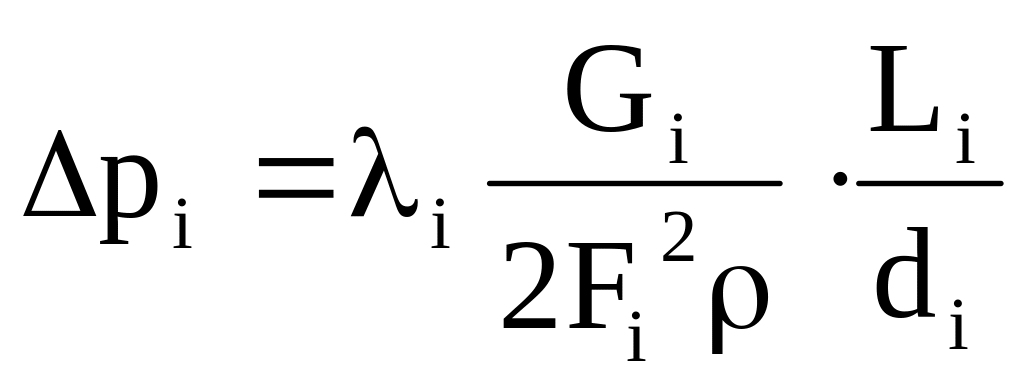(2)

Количество уравнений (2) будет равно количеству участков, т.е. 7.

Сумма всех количеств вещества, которое поступает в узел, равна количеству вещества, которое отбирается:

(3)

Сумма всех дебитов равна дебиту на выходе:

Запишем уравнение перепада давления для каждой ветви:

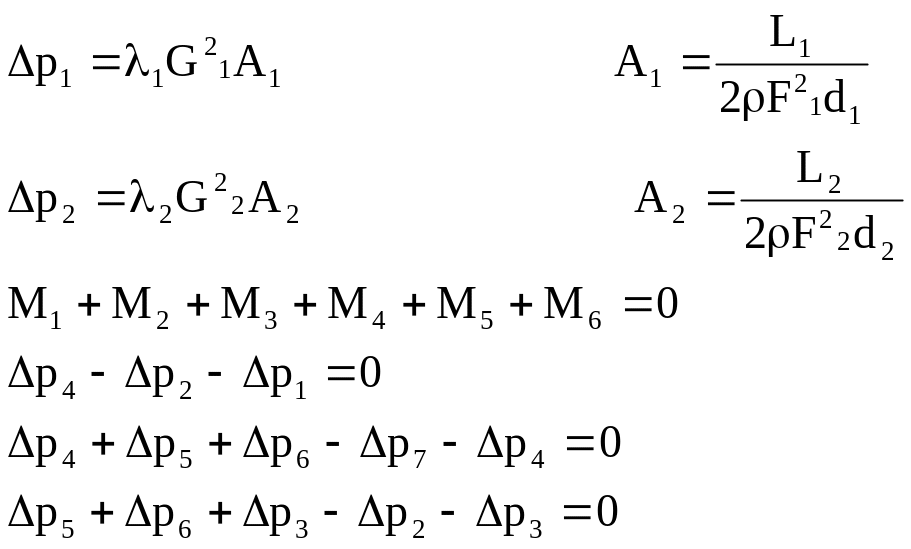
Закон перепадов давлений по замкнутому контуру:

Составляем систему из уравнений системы (2) – их 7 штук, системы (3) – их 6, и из уравнений (4) и (5). Получили систему из 15 уравнений, которая решается численными методами. Для ее решения нам также необходимо знать значение коэффициента гидравлического сопротивления, который является функцией числа Рейнольдса и других параметров.

Задача №8.

Построить математическую модель на основе экспериментальных данных.

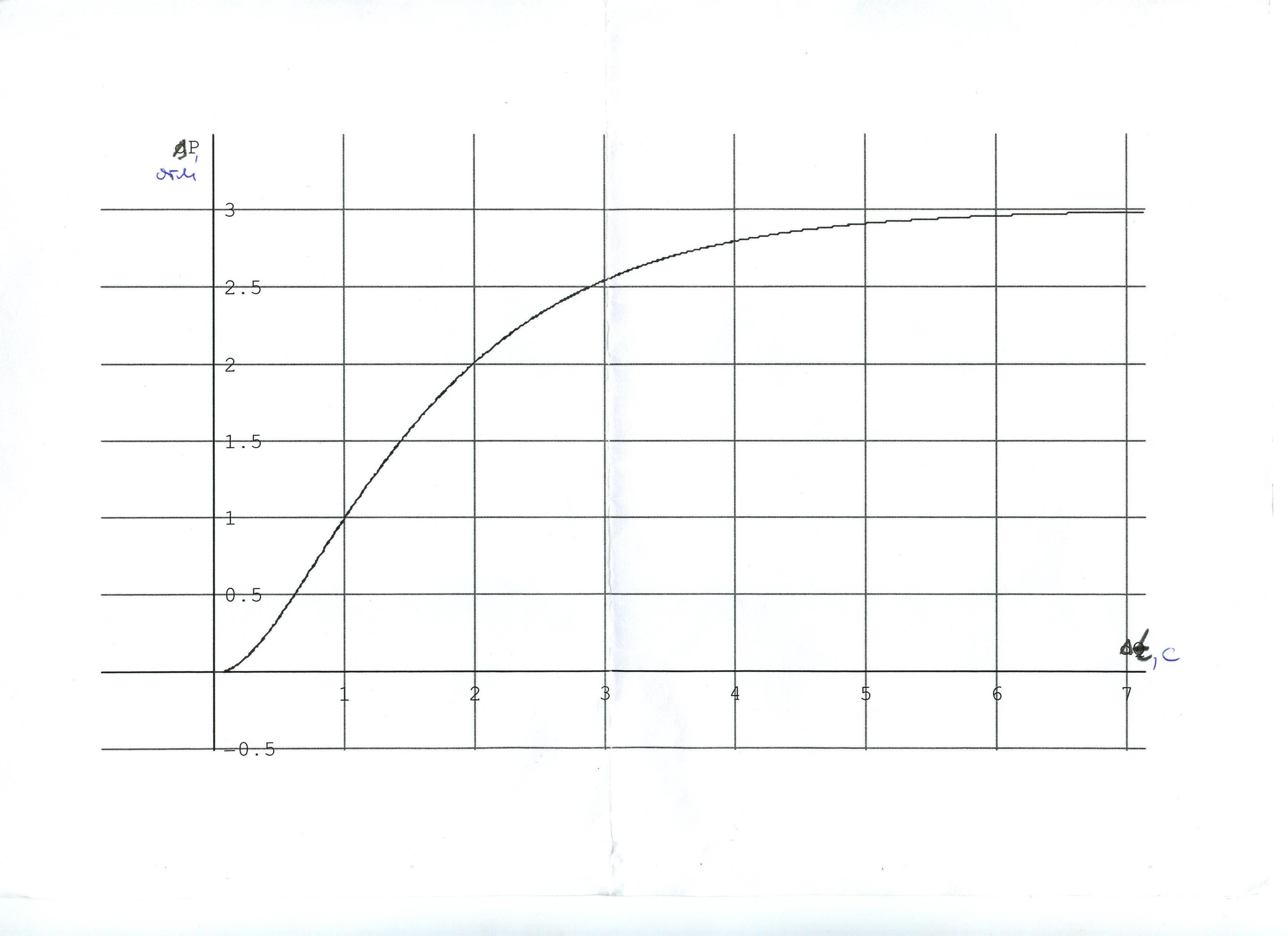
Рис.16. Кривая разгона, полученная экспериментально.

Требуется по кривой разгона идентифицировать технологический объект, то есть получить передаточную функцию методом площадей. Необходимо достигнуть точности в 5%.

Для дальнейшей работы необходимо нормировать и обезразмерить значение входного и выходного сигнала по формулам.

Значения взятых точек в первоначальном и в нормированном виде приведены в таблице 1.

В результате на входе получаем единичный скачок, а на выходе приведенное к единицы отклонение в безразмерном виде, показанное на рисунке 17.

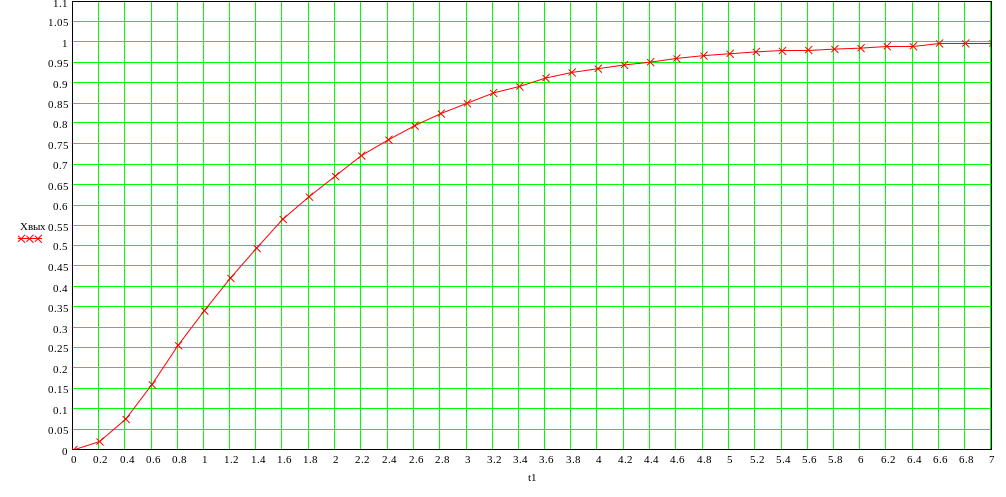Рисунок 17.Нормированный выходной сигнал.

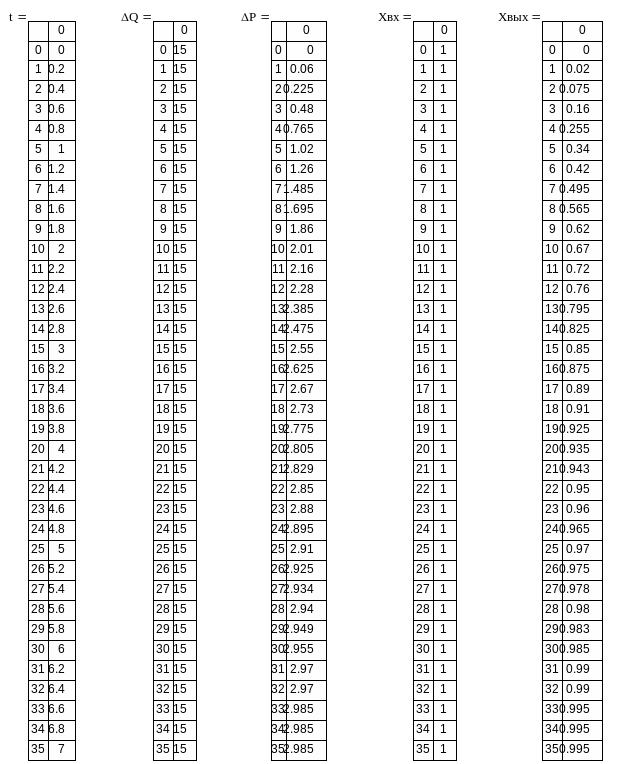
Таблица 1.

М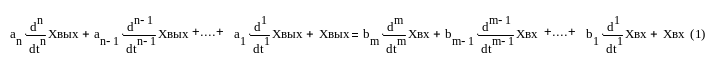 .П. Симою предложил способ определения передаточной функции объекта по графику его кривой разгона рис.16. Предположим, что исследуемый объект может быть описан линейным дифференциальным уравнением с постоянным коэффициентами.

где:

- постоянные коэффициенты.

Передаточная функция объекта, описываемого этим уравнением, может быть представлена в следующем виде:

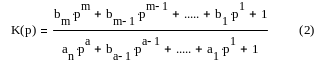
Задача состоит в том, чтобы определить неизвестные коэффициенты

Используя для этого следующую систему уравнений:

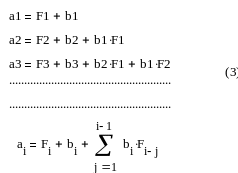
В этой системе уравнений i = m+n и для всех i > n a_i = 0 , а для i > m b_i = 0.

Входящие в уравнения коэффициенты F1,F2,…Fi вычисляются по следующим формулам:

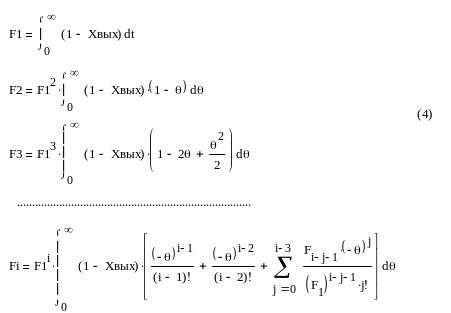
где θ = t / F1

Коэффициенты F1,F2,…Fi связаны с кривой разгона интегральными соотношениями, например для F1 это видно из рисунка 17.

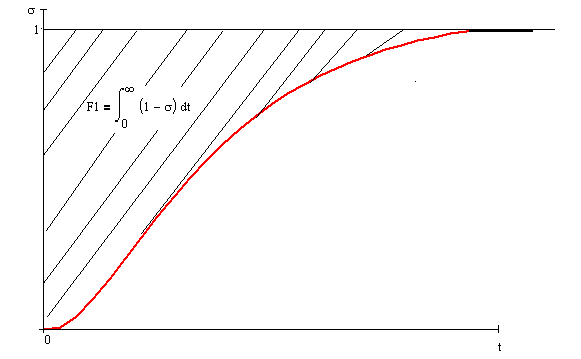
Рис.17. Определение F1 с помощью графика.

Многие промышленные технологические объекты имеют одну из следующих особенностей, влияющих на форму кривой разгона: объект характеризуется отсутствием транспортного запаздывания и наличием самовыравнивания; объект характеризуется отсутствием транспортного запаздывания и самовыравнивания; объект характеризуется наличием транспортного запаздывания и отсутствием или наличием самовыравнивания.

Имеется целый ряд технологических объектов, которые существенно отличаются по своим динамическим характеристикам от перечисленных выше типовых объектов. Их кривые разгона имеют более сложную форму, например не монотонную. Данная методика расчета неприменима для них.

Предположим, что объект является апериодическим звеном второго порядка. Его передаточная функция:

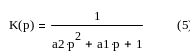
Выбираем интервал разбиения ∆t = 0.2 сек., исходя из условия, что на участке 2∆t функции X_вых мало отличаются от прямой. Выбранные точки приведены в таблице 5 (приведена в конце документа).

Определяем F1 по формуле:

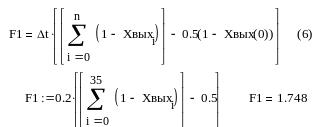
Определяем F2 по формуле:

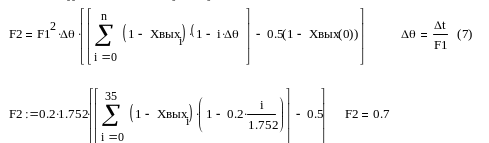
Так как b1=0 и b2=0, поэтом а1=F1=1,748 и а2=F2=0.7.

Передаточная функция объекта:

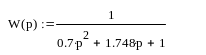
Найдем реакцию полученного объекта на единичный скачок и сравним ее с экспериментальной кривой разгона.

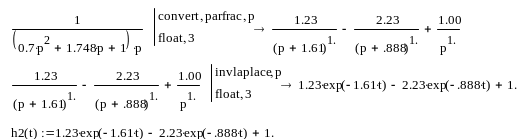
Построим переходную функцию полученного объекта и сравним ее с экспериментальной. Графики функций приведены на рисунке 18.

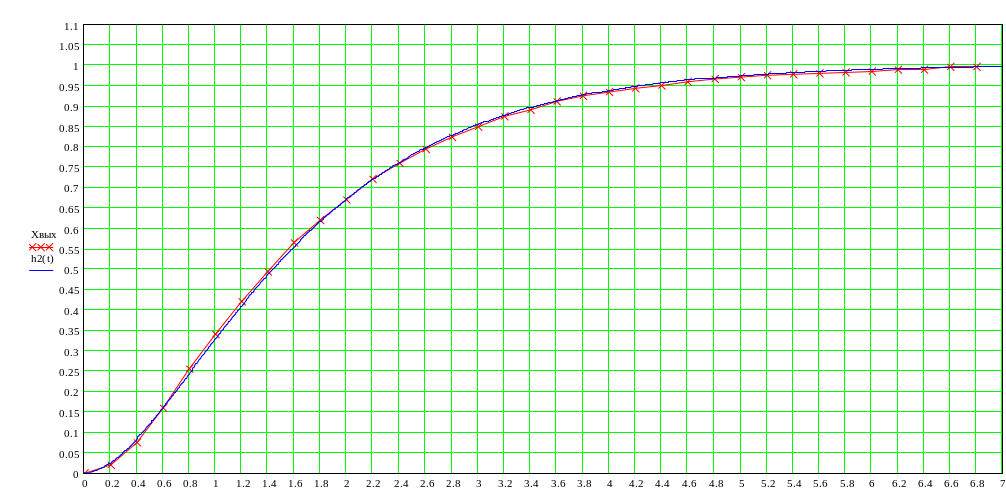
Рис.18 .Графики экспериментальной переходной функции и переходной функции, полученной с помощью метода площадей.

Погрешность 1,2%.

Задача №9.

Требуется по кривой разгона идентифицировать технологический объект, то есть получить передаточную функцию методом аппроксимации в классе экспоненциальных функций. Необходимо достигнуть точности в 5%.

Запишем переходную функцию в параметрическом виде.

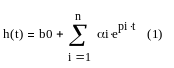
где α и р – неизвестные параметры.

Поскольку b0 может быть определен из экспериментальных данных, будем полагать, что b0 известно. Выделим из переходной функции свободную составляющую.

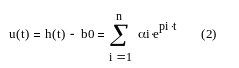
Величины α и р определяют на основе значений приближаемой функции y_i, измеренных в точках ti.

Запишем переходную функцию для данного объекта и выделим свободную составляющую.

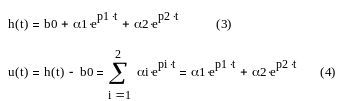
Выбираем 4 точки. Приравнивая поочередно эти значения, получим нелинейную систему уравнений относительно искомых параметров.

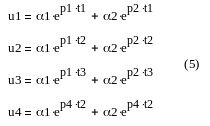
Выберем ti таким образом, чтобы

Перепишем систему (5):

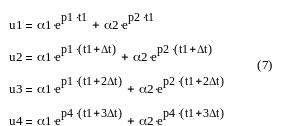
Сделаем замену переменных.

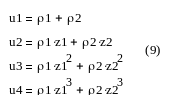
Введем вспомогательный характеристический многочлен:

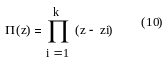
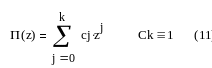
который равен нулю при z=zi.

Составляем вспомогательный многочлен. Для этого воспользуемся следующим приёмом. Умножим первое уравнение системы на С0, второе – на С1, третье – на С2.Полученные результаты сложим.

Предположим, что Z₁, Z₂ известны. Тогда они являются корнями какого-то многочлена

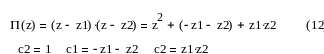
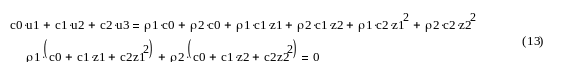
Получаем уравнение:

Умножим второе уравнение системы на С0, третье – на С1, четвертое – на С2.Полученные результаты сложим и получим уравнение.

В итоге получим линейную систему уравнений:

Находим с0,с1 и с2,подставляем в 12 и получаем z1,z2.Получаем значения рi используя формулу:

Получаем передаточную функцию:

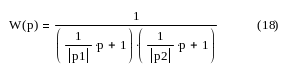
Возьмем четыре точки с шагом Δt=1 (таблица 2) и получим переходную функцию.

t, сек	Ui
0	-1
1	-0.66
2	-0.33
3	-0.15

Таблица 2.

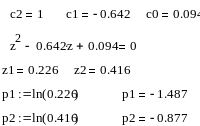
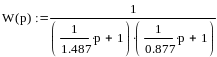
Построим переходную функцию полученного объекта и сравним ее с экспериментальной. Графики функций приведены на рисунке 20.

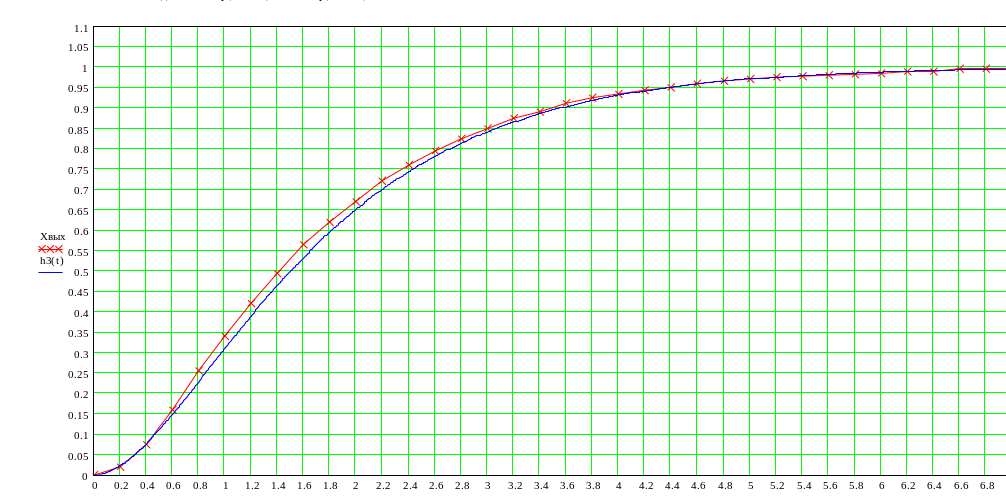
Рис.20. Графики экспериментальной переходной функции и переходной функции, полученной с помощью метода аппроксимации в классе экспоненциальных функций.