Задача №1.

Требуется построить математическую модель газовой емкости, схема которой представлена на рисунке 1. Через участок трубопровода, оборудованный задвижкой, природный газ поступает в емкость и отбирается через аналогичный участок трубопровода с задвижкой.

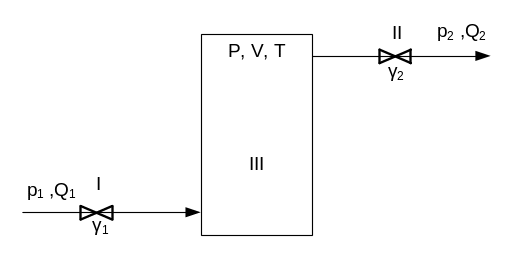
Рис.1 Газовая емкость

P – абсолютное давление в емкости

V – абсолютный объем емкости с газом

T – абсолютная температура в емкости

P1, Q1 – давление и массовый расход газа на входе в емкость

P2, Q2 – давление и массовый расход газа на выходе из емкости

1. γ - коэффициент, учитывающий гидравлическое сопротивление. Зависит от степени открытия задвижки, от температуры, от свойств пропускаемого вещества, от расхода, т.е. от скорости прохождения, от геометрических характеристик задвижки, от шероховатости.

Номинальный режим задается значениями:

Для удобства построения модели расходы Q1 и Q2 - массовые

1) Цель: понижение давления на выходе и его стабилизация

2) Проведем схематизацию объекта - выделим функционально завершенные части объекта: I. - участок трубопровода, оборудованный задвижкой

II. - участок трубопровода, оборудованный задвижкой

III. – емкость, заполненная природным газом

3) Примем ограничения и допущения, в рамках которых будет строиться модель

2. Исходя из особенности технологии и того, что имеется теплоизоляция емкости, допустим, что температура не меняется (или меняется незначительно), т.е. процесс можем считать изотермическим.

3. Примем, что объект с сосредоточенными параметрами (не зависят от координаты, меняются только во времени). Давление в емкости не зависит от координаты, т.к. объем емкости мал.

4. Содержание метана в природном газе обычно превышает 90%, поэтому взаимодействием молекул при данных термобарических условиях (обычно давление – несколько десятков атмосфер и температура близкая к нормальной) можно пренебречь, следовательно, свойства идеального и природного газа схожи, поэтому примем условие, что газ идеальный.

5. Примем, что процесс стационарный, т.е. за малые промежутки времени технологические параметры не изменяются в широких пределах.

4) Составим уравнение материального баланса на основе закона сохранения массы (количества вещества). Масса газа, поступающего в емкость за определенное время, равна массе газа, отбираемого за то же время:

(1) - статический режим

5) Составим уравнение динамики. Запишем изменение массы газа внутри емкости за время :

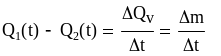(2) - динамический режим

Разность расходов на входе и выходе равно изменению массы газа внутри емкости

6) Запишем данное уравнение, выразив все слагаемые через технологические параметры:

Где:

- потери давления на 1й и 2й задвижках соответственно.

Запишем уравнение состояния идеального газа, в силу принятых ограничений и допущений (уравнение Менделеева– Клайперона):

(5)

Где M – молярная масса

R – универсальная газовая постоянная

Изменение массы связано только с изменением давления:

(6)

Подставим все найденные параметры в выражение (2)

(7)

Перейдем от приращений к производным

(8)

Получили дифференциальное уравнение изменения давления в газовой емкости. Далее нормируем и обезразмерим функции.

Видим, что в правой части уравнения есть нелинейные функции. Линеаризуем их. Разложим в ряд Тейлора вблизи рабочей точки (номинального режима) до первого слагаемого:

(9)

(10)

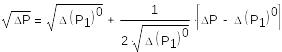
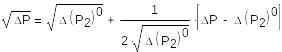
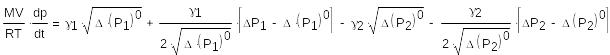
(11)

где

- в номинальном режиме расходы равны

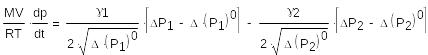
(12)

Введем безразмерные и нормированные функции входа и выхода:

(13)

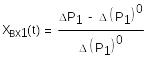
(14)

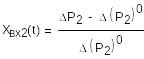
(15)

Подставим полученные выражения в (11):

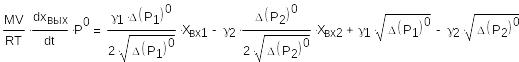
(16)

Из номинального режима получаем:

(17)

Тогда можем переписать уравнение:

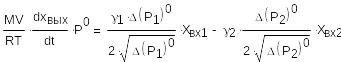
(18)

Разделив обе части уравнения на коэффициент при х_вх2 , получим:

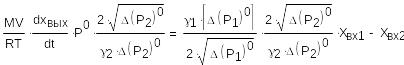
(19)

Введем обозначения:

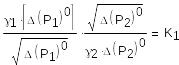
- безразмерный коэффициент

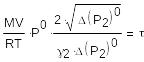
- постоянная времени, имеет размерность секунды

Можем переписать наше уравнение:

(20)

Начальные условия:

(21)

Уравнение (20) с начальными условиями (21) и есть искомая математическая модель газовой емкости.

Найдем передаточную функцию и построим структурную схему.

- интегрирующее звено (22)

Рис.2

Теперь предположим, что:

как было задано в условии

Тогда разложение в ряд Тейлора будет выглядеть следующим образом:

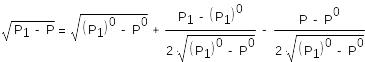
(23)

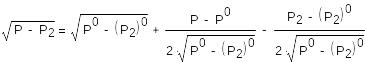
(24)

Проведя преобразования, аналогичные преобразованиям (11) – (17), получим уравнение:

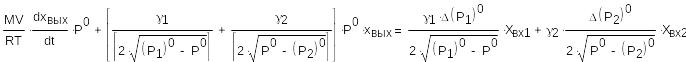
(25)

где:

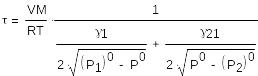
- постоянная времени, имеет размерность секунд.

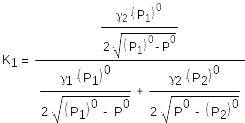
- безразмерный коэффициент

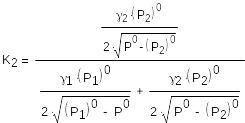
- безразмерный коэффициент

Передаточная функция объекта:

- апериодическое звено. (26)

Изобразим структурную схему:

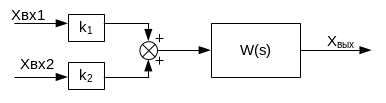
Рис.3

Задача №2.

Необходимо построить математическую модель емкости с жидкостью, схема которой представлена на рисунке 4.

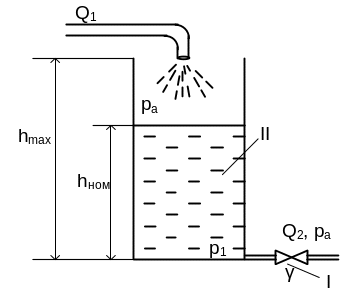
Рис.4

I – участок трубопровода с гидравлическим сопротивлением

II – емкость, наполненная жидкостью

Q1 и Q2 – объемные расходы на входе и выходе емкости

Pa – атмосферное давление

P1 – давление на дне емкости

hmax – максимальный уровень жидкости в емкости (h _m)

hном – номинальный уровень жидкости в емкости (h⁰)

Номинальный режим задается значениями: P₁⁰, Q₁⁰, Q₂⁰.

Ограничения и допущения.

1. Объект с сосредоточенными параметрами. Давление в емкости, которое в данном случае зависит от координаты, нас интересует в одной конкретной точке(точка отбора).

2. Идеальная жидкость, т.е. несжимаемая.

3. Стационарный процесс.

Запишем закон сохранения массы:

(1)

Т.к. жидкость идеальная, т.е. плотность не изменяется, можем в равенстве(1) использовать объемные расходы

Тогда изменение объема жидкости внутри емкости за время будет равно:

2. - уравнение материального баланса

(3)

Где :

S – площадь поперечного сечения емкости

h – уровень жидкости в емкости

Выражаем все слагаемые через технологические параметры:

(4)

(5) - Закон Архимеда

(6)

Начальные условия:

При t=0: h(t)=h⁰

Q₁⁰ = Q₂⁰

_{Можем переписать уравнение (3):}

(7)

Линеаризуем правую часть уравнения в окрестности рабочей точки. Разложим её в ряд Тейлора до первого члена :

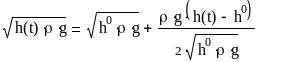
(8)

Подставим выражение (8) в уравнение (7) и приведем к безразмерному виду:

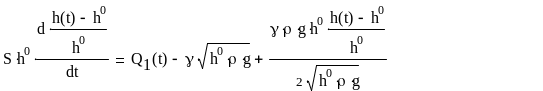
(9)

( 10)

Тогда перепишем:

(11)

Введем безразмерные нормированные функции:

(12) -выход

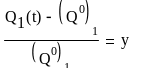
(13) -вход

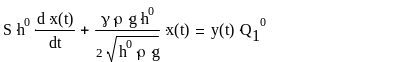
(14)

Разделим обе части уравнения на коэффициент при Х:

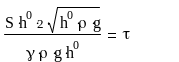
- постоянная времени, имеет размерность времени

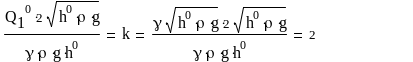(15)

Получили уравнение:

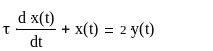
(16)

С начальными условиями:

Х(0)=0;

Y (0)=0.

Передаточная функция:

Структурная схема:

Рис.5

Задача №3.

Требуется построить математическую модель химического реактора идеального смешивания и получить графики зависимости концентрации веществ от времени нахождения в реакторе.

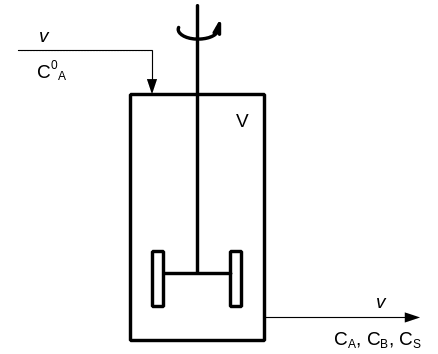
Рис.6

v – объемная скорость

V – объем реактора

- время нахождения части вещества внутри реактора

Рассмотреть 3 случая:

1. В реактор поступает вещество А, на выходе получаем вещество Р, реакция обратимая:

(1) скорость 1й стадии

(2) скорость 2й стадии

Найти:

2. На вход реактора поступает вещество А, из него образуется вещество P и вещество S:

2. с корость 1й стадии

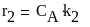2. с корость 2й стадии

Найти :

3. на вход поступает вещество А, из него образуется вещество P, а из Р образуется вещество S.

(5)

(6)

Найти концентрации всех веществ.

Ограничения и допущения.

1. Идеальное перемешивание (параметры становятся одинаковыми во всех точках в зоне идеального смешивания)

2. Объект с сосредоточенными параметрами (не зависят от координаты, меняются во времени. Т.к. емкость мала, концентрация распространяется по всему объему).

3. Процесс стационарный (параметры не изменяются в широком диапазоне в течении малого промежутка времени).

4. Процесс изотермический, т.е. коэффициенты К1 и К2 постоянные.

Диффузия – проникновение молекул одного вещества в межмолекулярное пространство другого.

В процессе конвекции перемешиваются слои или части веществ.

Запишем общее уравнение:

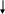
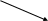(7)

диффузионный конвективный за счет химической реакции

механизм

Концентрация не зависит от координаты, поэтому все производные по координате обращаются в ноль. Получаем:

изменение количества вещества за время .

Пусть на вход поступает элементарный объем , тогда получаем:

(8)

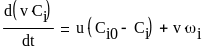
(9), где

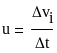
- объемная скорость. (10)

Поделим обе части уравнения на V:

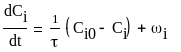
(11)

Рассмотрим 1й случай.

Решаем задачу в статическом режиме (производная по времени обращается в ноль):

(12)

(13) - скорость образования вещества А

Подставляем (13) в (12):

(14)

Т.к. сумма концентраций в любой момент времени постоянна, то запишем:

(15)

Подставляем выражение (15) в (14):

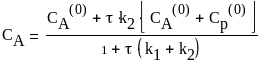
(16)

При:

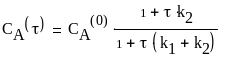
(17)

Подставим Са в выражение для Ср, получим:

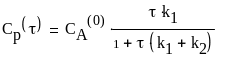
(18)

Построим графики зависимости концентрации веществ от времени пребывания в реакторе:

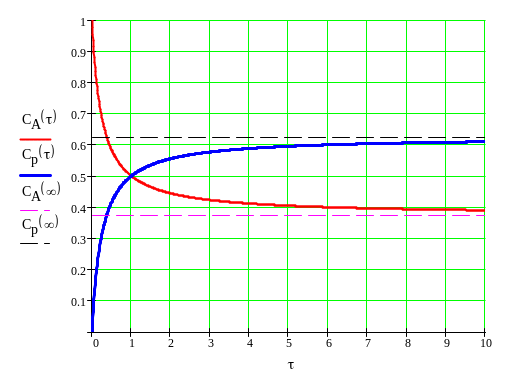
Рис. 7

Рассмотрим 2й случай.

(19)

(20)

В статическом режиме:

(21)

Решая систему (21), получим:

(22) концентрация вещества А

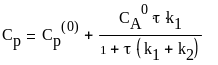
(23) концентрация вещества Р

В частном случае, когда получаем выражение для концентрации вещества Р:

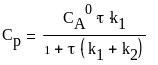
(24)

Т.к. концентрация сохраняется:

(25)

Найдем из выражения (25) концентрацию вещества S:

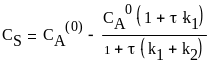
(26)

Построим графики зависимости концентрации веществ от времени пребывания в реакторе:

Рис.8

Рассмотрим 3й случай.

( 27) скорость образования вещества А

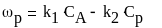28. с корость образования вещества P

В статическом режиме:

(29)

Из системы (29) находим концентрации веществ А и Р:

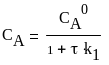
(30)

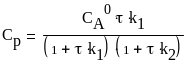
(31)

Запишем скорость образования вещества S:

(32)

Запишем общее уравнение для вещества S:

(33)

Подставим (32) в (33) и учтем, что начальная концентрация вещества S равна нулю:

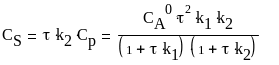
(34)

Построим графики зависимости концентрации веществ от времени пребывания в реакторе (для построения графиков необходимо исследовать функции Cs и Cp на экстремум):

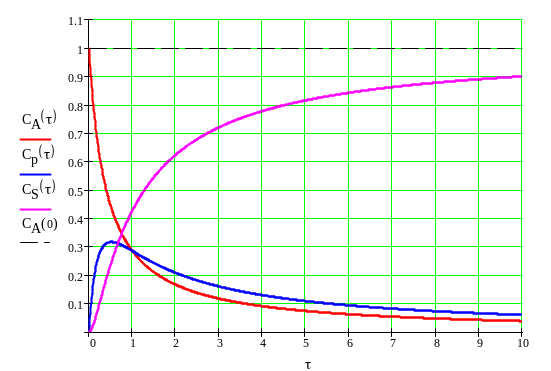
Рис.9

Задача №4.

Требуется построить математическую модель теплообменника типа «смешение - смешение» и определить оптимальную площадь поверхности теплообмена.

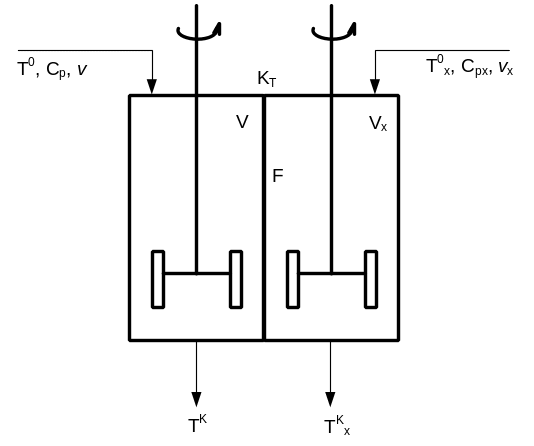
Рис.10

KT – коэффициент теплопередачи

F – поверхность теплообмена

V – объем камеры с теплоносителем

Vх – объем камеры с хладагентом

Cp – теплоемкость теплоносителя

Cpх – теплоемкость хладагента

– температура теплоносителя на входе

– температура хладагента на входе

– температура теплоносителя на выходе

– температура хладагента на выходе

v – объемная скорость теплоносителя

vх – объемная скорость хладагента

Теплообменник представляет собой камеру, разделенную перегородкой на две части, в каждой из которых происходит процесс идеального смешивания. В первой находится теплоноситель - более нагретое вещество, во второй – хладагент. На выходе температура конечная. Идеальное смешивание – параметры мгновенно становятся одинаковыми при попадании в зону идеального смешивания (температура становится конечной).

Допущения и ограничения.

1. Объект с сосредоточенными параметрами, т.к. в зоне идеального смешивания параметры одинаковы, не зависят от координаты.

2. Идеальная теплоизоляция от внешней среды.

3. Теплоемкость поверхности теплообмена пренебрежительно мала по сравнению с теплоемкостью веществ.

4. Тепловой поток через стенку устанавливается мгновенно. Тепловой поток от теплоносителя к хладагенту перпендикулярен поверхности теплообмена.

5. Давление постоянно.

6. Процессы стационарные.

7. Нет внешних и внутренних источников тепла

8. Постоянный коэффициент теплопередачи (поверхность однородная) Kt=const.

Запишем уравнение теплового баланса в статическом режиме. Для этого введем обозначения:

- количество тепла, передаваемое от теплоносителя к хладагенту в процессе теплообмена.

- количество тепла, поступающее в 1ю камеру с теплоносителем

- количество тепла, поступающее во 2ю камеру с хладагентом

- количество тепла, которое отбирается вместе с теплоносителем

- количество тепла, которое отбирается вместе с хладагентом

(1) для теплоносителя

(2) для хладагента

В динамическом режиме:

для теплоносителя

(3)

для хладагента

(4)

(5)

(6)

(7)

(8)

( 9)

Решим вопрос о механизме теплообмена:

Рассмотрим три вида механизмов теплообмена

1. Лучистый.

Излучение характеризуется тем, что всегда есть источник энергии, который с помощью электромагнитных волн передает энергию (тепло). Источник тепла: объект, который преобразует один вид энергии в другой. В данном случае нет источника тепла, соответственно нет и излучения.

2. Конвекция.

Перемешивание частиц слоев вещества

Нет конвекции, т.к. есть твердая перегородка и параметры одинаковы.

3. Теплопередача.

Теплопередача осуществляется засчет свойства теплопроводности веществ, которое реализуется в результате хаотичного теплового движения частиц внутри вещества.

Запишем тепловой поток через поверхность теплообмена:

(10)

Тогда количество тепла, передаваемое от теплоносителя к хладагенту, будет равно:

(11)

Перепишем систему (3) с учетом выражений (4) – (11):

(12)

(13)

Делим обе части уравнений на :

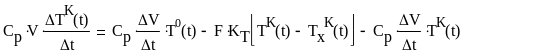
(14)

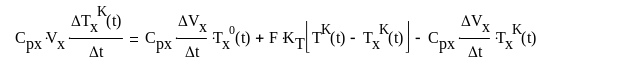(15)

- объемная скорость теплоносителя (16)

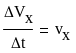
- объемная скорость хладагента (17)

Учитывая (16) (17), перепишем:

(18)

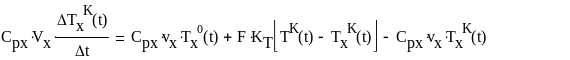
(19)

Преобразуем, приведя подобные слагаемые, и запишем систему в статическом режиме:

(20) для теплоносителя

( 21) для хладагента

Примем неизвестными площадь поверхности теплообмена и конечную температуру теплоносителя.

Сложим уравнения (20) и (21):

Н айдем конечную температуру теплоносителя:

Подставим конечную температуру теплоносителя в выражение (20) и найдем площадь поверхности теплообмена:

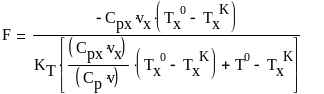
(24)

Найдем оптимальную площадь поверхности теплообмена, для этого будем менять любой из параметров, например vx. Возьмем производную по vx и найдем минимальную площадь:

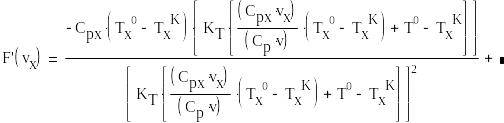
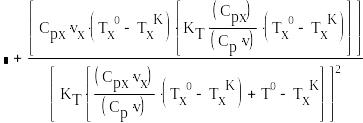
(25)

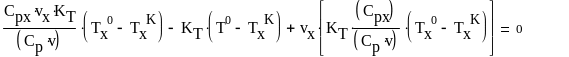
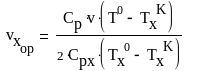
(28)

Теперь подставим (28) в (24):

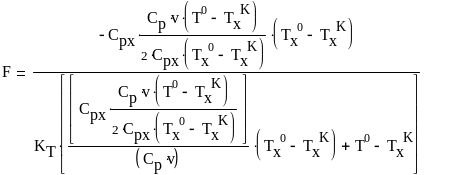
(29)

Сокращаем и получаем оптимальную площадь поверхности теплообмена:

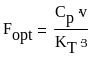
(30)

Задача №5.

Требуется построить математическую модель теплообменника типа «труба – труба» и изобразить графики изменения температуры по длине теплообменника.

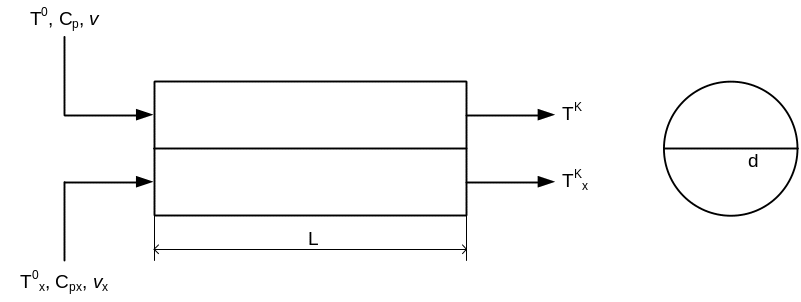
Рис.11

Теплообменник представляет собой трубу, которая разделена перегородкой. В одну камеру поступает теплоноситель со своими параметрами, в другую – хладагент. По длине теплообменника происходит процесс идеального вытеснения. Идеальное вытеснение – процесс, при котором температура меняется только по координате х.

Cp – теплоемкость теплоносителя

Cpх – теплоемкость хладагента

– температура теплоносителя на входе

– температура хладагента на входе

– температура теплоносителя на выходе

– температура хладагента на выходе

v – объемная скорость теплоносителя

vх – объемная скорость хладагента

L – длина теплообменника

d – диаметр теплообменника