41. Геометрический смысл уравнения Бернулли.

Все члены, входящие в уравнение Д. Бернулли, имеют ли­нейную размерность, поэтому их принято называть высотами. Соответственно общеприняты следующие названия для этих членов:

z - геометрическая или геодезическая высота;

- пьезометрическая высота или высота давления;

– динамический или скоростной напор;

Легко усмотреть следующий геометрический смысл урав­нения Д. Бернулли, который заключается в том, что при установившемся движении идеальной жидкости сумма трех высот (геометрической, пьезометрической и скоростной) не меняется вдоль данной элементарной струйки. Это положение наглядно иллюстрируется на рис. 1.

Можно трактовать смысл отдельных членов уравнения

Бернулли иначе. Выше было показано, что сумма

представляет собой удельную энергию жидкости. В соответст­вии с этим можно считать, что:

z - есть удельная энергия положения;

- энергия давления;

- есть удельная кинетическая энергия.

42. Энергетический смысл уравнения Бернулли.

Э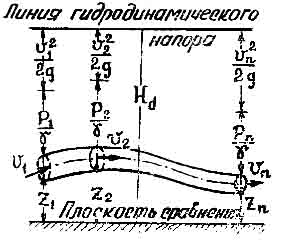 нергетический смысл уравнения Бернулли заключается в том, что при установившемся движении идеальной жидкости сумма удельных энергий положения, давления и кинетиче­ской не меняется вдоль данной элементарной струйки.

Р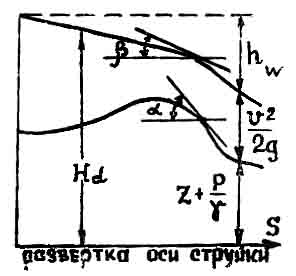 ис. 1

Полная удельная энергия (т. е. потенциальная + кинетиче­ская) называется гидродинамическим напором и обозначается . Таким образом, уравнение Бернулли пока­зывает, что при установившемся движении идеальной жидкости для данной струйки гидродинамический напор есть величина постоянная. На графике линия гидродинамического напора изображается горизонтальной линией.

43. Уравнение Бернулли для элементарной струйки реальной жидкости.

П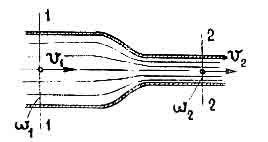 ри движении реальной жидкости между соседними струйками возникают силы трения, на преодоление которых затрачивается часть энергии жидкости. Поэтому удельная энергия жидкости в сечении элементарной струйки 2—2 будет менее удельной энергии жидкости в сечении 1—1 на некото­рую величину , которую называют потерянной высотой или потерянной удельной энергией, затрачиваемой на преодоление гидравлических сопротивлений. Аналитически это положение запишется таким образом:

Следовательно, при установившемся движении реальной жид­кости сумма четырех высот (геометрической, пьезометрической, скоростной и потерянной) или, что то же самое, сумма четырех удельных энергий (положения, давления, кинетиче­ской и потерянной) не изменяется вдоль данной элементар­ной струйки.

Легко изобразить уравнение Бернулли для рассматри­ваемого случая графически. Для этого следует, выбрав произвольную горизонтальную плоскость сравнения, отложить на ней в каждом сечении высоты ; ; ; и . Концы отрезков z, соединенные плавной кривой, покажут положение оси струйки. Соединяя концы отрезков плавной кривой, получим так называемую пьезометрическую линию. Отложив в каждом сечении вверх от пьезометрической линии отрезки, равные скоростным напорам , и соединив их концы плавной кривой, получим линию гидро­динамического напора или, как ее часто называют, гидравличе­скую линию (рис. 2). Отрез­ки, равные расстояниям по вер­тикали от гидравлической ли­нии до горизонтальной плоско­сти, проходящей над плос­костью сравнения на высоте, равной начальной удельной энергии, представляют собой потери энергии на гидравличе­ские сопротивления на участке от начального до рассматриваемого сечения.

Рис. 2

Падение гидравлической линии на единицу длины элементарной струйки назовем гидравлическим уклоном I:

Гидравлический уклон (рис.3) есть всегда величина положитель­ная, так как полная удельная энергия движущейся части жидкости постепенно умень­шается по мере ее продвижения вдоль элементарной струйки, затрачиваясь на преодоление сил трения, превращаясь в теп­ловую энергию и рассеиваясь.