3.2. Проверка ошибок при оценке дисперсии

Для того, чтобы проверить возможные ошибки при оценке дисперсии исходной генеральной совокупности, имея две группы данных (выборка которых была сделана независимо друг от друга) и предполагая, что они получены из одной генеральной совокупности можно основываться на таблице распределения Фишера (F-распределение). При этом, сравнивая значение F₀, вычисленное из данных, с сопоставимыми значениями из таблиц F-распределения, принимают решение отклонить или принять нулевую гипотезу.

Таблица F-распределения составлена так, что большая несмещенная оценка дисперсии принимается за числитель. Следует также иметь в виду то, что таблица предназначена для односторонней проверки и если понадобится проводить двухстороннюю проверку соотношения дисперсий при уровне значимости , то используют значения таблицы F-распределения для  (рис.3.1).

Порядок проверки гипотезы:

1. Строят нулевую гипотезу:

Н₀:_е1² = _е2².

2. Строят альтернативную гипотезу:

Н₁:_е1²  _е2² (двухсторонняя проверка),

_е1²  _е2² или _е1²  _е2² (односторонняя проверка).

3. Определяют несмещенные дисперсии _е1², _е2² из каждой выборки:

_е1² = S₁/Ф₁, Ф₁ = n₁ - 1, (3.3)

_е2² = S₂/Ф₂, Ф₂ = n₂ - 1. (3.4)

4. Определяют соотношение несмещенных оценок дисперсии F₀. В данном случае большее из двух _е1², _е2² принимается за числитель. Если _е1²  _е2², то определяется величина:

F₀ = _е1²/_е2².

5. Если за уровень значимости принять , то при двухсторонней проверке из табл.3 Приложения определяют значение F_ф1, _ф2, /2.

6. Выносят решение. Если: F₀  F_ф1, _ф2, /2, то принимают Н₀ и считают, что в оценке дисперсии расхождений нет.

Если же F₀  F_ф1, _ф2, /2, то принимают Н₁ и считают, что в оценке дисперсии имеется расхождение.

Пример 3.3.

Измерив по шкале С Роквелла значение твердости после закалки, произведенной на высокочастотных закалочных устройствах А и В, получили следующие данные для каждого из них:

Устройство А	53,5	54,0	53,8	54,5	54,8
Устройство В	54,8	53,0	52,8	54,0	53,5	54,5

Можно ли утверждать, что в оценке рассеивания значений имеется расхождение?

1. Н₀:_А² = _В²

2. Н₁:_А²  _В².

3. По формуле (2.3) определяют сумму квадратов отклонений:

4. Определяют несмещенные оценки дисперсии:

_А² = S_А/Ф_А = 1,11/4 = 0,2775

_В² = S_В/Ф_В = 3,25/5 = 0,650.

5. Определяют отношение дисперсий:

F₀ = _B²/_A² = 0,650/0,2775 = 2,34.

6. Сравнивают предельные значения из таблицы F-распределения (табл.3 Приложения) с F₀.

F_5;4;0,025 = 9,36  F₀.

7. Выносят решение. Принимается нулевая гипотеза Н₀, поскольку расхождения в оценках дисперсии от применения этих двух устройств не существенны.

3.3. Проверка различия средних арифметических

Обычно при сравнении существующего технологического процесса с усовершенствованным технологическим процессом, при сравнении производственной методики по способу А и В, при сопоставлении результатов работы группы А и группы В и т.д. среднее генеральной совокупности часто бывает неизвестно. В такого рода ситуациях рекомендуется осуществлять проверку, придерживаясь следующего порядка.

Прежде всего, определяют отношение дисперсий, полученных из несмещенных оценок _е1², _е2² для двух групп выборок, и осуществляют проверку по F-распределению, в результате чего убеждаются, что в дисперсии не обнаруживается существенного различия. В том случае, когда между _е1² и _е2² имеется существенное различие, то определить общую дисперсию ₂² становится невозможным.

Если нет существенного различия между _е1² и _е2², то обозначая средние арифметические измеренных значений двух групп выборок n₁, n₂ через , а сумму квадратов через S₁, S₂, можно построить предположение, что дисперсия генеральной совокупности ² оценивается общей для двух групп несмещенной оценкой :

= (3.6)

При проверке существенного различия средних арифметических в двух группах выборок целесообразно применить формулу:

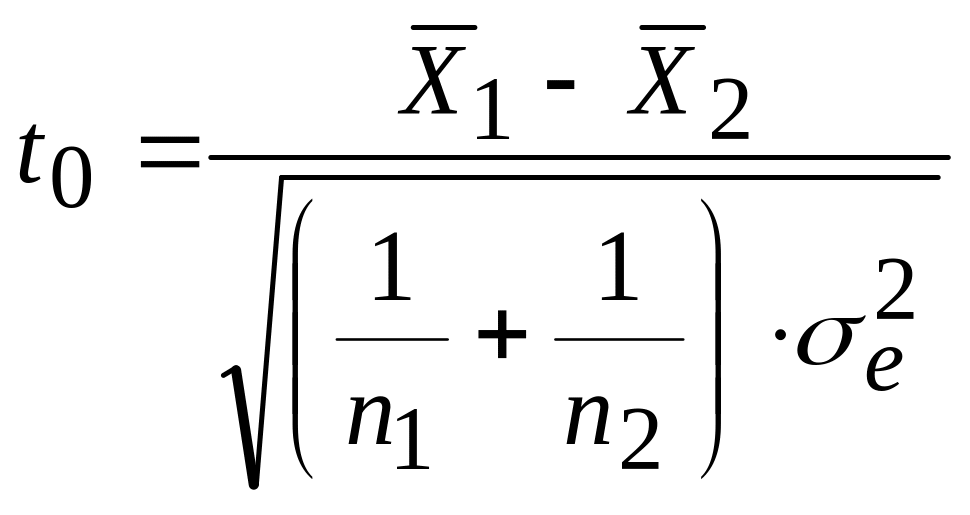(3.7)

и осуществлять проверку по t-распределению. При этом число степеней свободы равно Ф = n₁+n₂ - 2.

Объединив вместе все процедуры проверки при данной ситуации, получают:

1. Н₀:₁² = ₂², а также ₁ = _2.

2. Определяют дисперсии _е1², _е2² и осуществляют проверку по

F-критерию. Если нет существенного различия переходят к следую-

щему процессу.

3. Н₁:₁  ₂.

4. Определив _е², вычисляют t₀.

5. Сравнив t₀ со значениями t_ф, из таблицы t-распределения при

Ф = n₁+n₂ - 2, делают выводы.

Пример 3.4.

Проверить, существенно ли различие в средних значениях твердости после закалки, произведенной на устройствах А и В, пользуясь данными примера 3.3.

Решение:

1. Н₀:_А² = _В², _А = _В.

2. В результате проверки по F-критерию, как уже было описано выше, существенного различия не было установлено.

3. Н₁:_А  _В.

4. Определяют несмещенную оценку дисперсии по зависимости (2.6):

5. Вычисляют по выражению (3.7) t₀:

6. Выносится решение:

t_9;0.01 = 3.25  t_0.

Существенного различия между средними значениями не установлено.