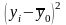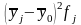2.2. Измеряем тесноту корреляционной связи между названными признаками с использованием коэффициентов детерминации и эмпирического корреляционного отношения.

Рассчитываем эмпирический коэффициент детерминации 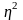и эмпирическое корреляционное отношение .

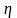Эмпирический коэффициент детерминации оценивает силу связи, определяя, насколько вариация результативного признака Y объясняется вариацией фактора Х. Показатель рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле

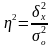, (9)

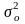– общая дисперсия признака Y,

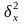– межгрупповая (факторная) дисперсия признака Y.

Значения изменяется в пределах 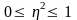. Если нет корреляционной связи между признаками Х и Y, то = 0, если функциональная связь есть, то = 1.

Общая дисперсия характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Формула:

, (10)

y_i – индивидуальные значения результативного признака;

– общая средняя значений результативного признака;

n – число единиц совокупности.

Общая средняя вычисляется как средняя арифметическая простая по всем единицам совокупности:

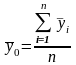(11)

или как средняя взвешенная по частоте групп интервального ряда:

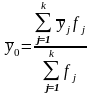(12)

Поскольку в таблице 8 есть значения числителя и знаменателя формулы (11), то используем её для вычисления :

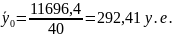
Для расчёта общей дисперсии строим дополнительную таблицу 12.

Таблица 12

Вспомогательная таблица для расчета общей дисперсии

Номер квартиры п/п	Цена 1 кв.м общей площади, у.е.
1	2	3	4	5
1	361,1	68,69	4718,316	130393,210
2	186,7	-105,71	11174,604	34856,890
3	177,6	-114,81	13181,336	31541,760
4	406,4	113,99	12993,720	165160,960
5	310,2	17,79	316,484	96224,040
6	321,0	28,59	817,388	103041,000
7	390,4	97,99	9602,040	152412,160
8	187,3	-105,11	11048,112	35081,290
9	403,1	110,69	12252,276	162489,610
10	433,3	140,89	19849,992	187748,890
11	187,3	-105,11	11048,112	35081,290
12	386,1	93,69	8777,816	149073,210
13	138,9	-153,51	23565,320	19293,210
14	481,4	188,99	35717,220	231745,960
15	256,2	-36,21	1311,164	65638,440
16	266,9	-25,51	650,760	71235,610
17	117,0	-175,41	30768,668	13689,000
18	293,9	1,49	2,220	86377,210
19	500,0	207,59	43093,608	250000,000
20	350,0	57,59	3316,608	122500,000
21	405,2	112,79	12721,584	164187,040
22	210,5	-81,91	6709,248	44310,250
23	193,3	-99,11	9822,792	37364,890
24	437,5	145,09	21051,108	191406,250
25	267,8	-24,61	605,652	71716,840
26	340,9	48,49	2351,280	116212,810
27	394,9	102,49	10504,200	155946,010
28	266,7	-25,71	661,004	71128,890
29	157,9	-134,51	18092,940	24932,410
30	359,2	66,79	4460,904	129024,640
31	286,1	-6,31	39,816	81853,210
32	380,8	88,39	7812,792	145008,640
33	284,2	-8,21	67,404	80769,640
34	350,0	57,59	3316,608	122500,000
35	392,5	100,09	10018,008	154056,250
36	480,5	188,09	35377,848	230880,250
37	402,8	110,39	12185,952	162247,840
38	394,1	101,69	10340,856	155314,810
39	350,1	57,69	3328,136	122570,010
40	363,0	70,59	4982,948	131769,000
Итого	11 696,4	1 176,4	428656,848	4536783,420

Расчет общей дисперсии по формуле (10):

Общую дисперсию можно рассчитать также по формуле

,

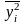– средняя из квадратов значений результативного признака,

– квадрат средней величины значений результативного признака.

Межгрупповая дисперсия измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х. вычисляется по формуле

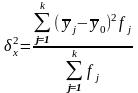, (13)

–групповые средние

– общая средняя,

–число единиц в j-ой группе,

k – число групп.

Для расчета межгрупповой дисперсии строим вспомогательная таблица 13. Средние значения берём из таблицы 9.

Таблица 13

Вспомогательная таблица для расчета межгрупповой дисперсии

Группы квартир по цене 1 кв.м общей площади квартиры	Число квартир,	Среднее значение в группе
1	2	3	4	5
1	8	427,45	135,04	145886,413
2	10	363,55	71,14	50608,996
3	7	288,54	-3,87	104,838
4	6	285,22	-7,19	310,177
5	5	233,48	-58,93	17363,725
6	4	229,8	-62,61	15680,048
Итого	40			229 954,197

Расчет межгрупповой дисперсии по формуле (13):

Рассчитаем эмпирический коэффициент детерминации по формуле (9):

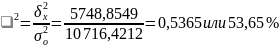
Вывод. 53,7% вариации цены 1 кв.м общей площади квартиры обусловлено вариацией рейтинга района города по удалённости от центра, а 46,3% – влиянием прочих неучтенных факторов.

Эмпирическое корреляционное отношение оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле

(14)

Значение показателя изменяются в пределах 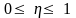. Чем ближе значение к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе служит шкала Чэддока (таблица 14):

Таблица 14

Шкала Чэддока

	0,1 – 0,3	0,3 – 0,5	0,5 – 0,7	0,7 – 0,9	0,9 – 0,99
Характеристика силы связи	Слабая	Умеренная	Заметная	Тесная	Весьма тесная

Расчет эмпирического корреляционного отношения по формуле (14):

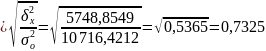
Вывод. Согласно шкале Чэддока связь между ценой 1 кв.м общей площади квартиры и рейтингом района города по удалённости от цента является тесной.

Проверяем статистическую значимость . Рассчитанное значение F-критерия F_расч сравниваем с F_табл (по таблице распределения Фишера).

n – число единиц выборочной совокупности,

m – количество групп,

– межгрупповая дисперсия,

– дисперсия j-ой группы (j=1,2,…,m),

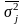– средняя арифметическая групповых дисперсий

Величина рассчитывается, исходя из правила сложения дисперсий:

,

где 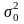– общая дисперсия.

=

F_{табличное}(0,05; 5;34) = 2,49

n	m	k1=m-1	k2=n-m	Fтабл ( ,6, 34)
40	6	5	34	2,49

7,87>2,49. Вывод: поскольку F_расчF_табл, то величина коэффициента детерминации =53,7% признается значимой (неслучайной) с уровнем надежности 95%. Следовательно, найденные характеристики связи между признаками Цена 1 кв. м общей площади квартиры и Рейтинг района города по удалённости от центра правомерны не только для выборки, но и для всей генеральной совокупности квартир.