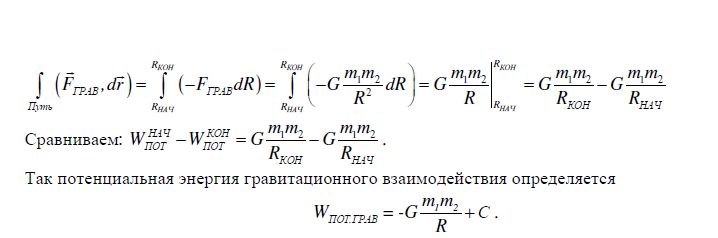- •Билет №1 Вопрос №1.
- •Вопрос №2.
- •Билет №5 Вопрос №1.
- •Вопрос №2.
- •Билет №16
- •Билет №17
- •Билет №18
- •Билет №19
- •Вопрос 2 )Коэффициент силы трения скольжения
- •Билет №20
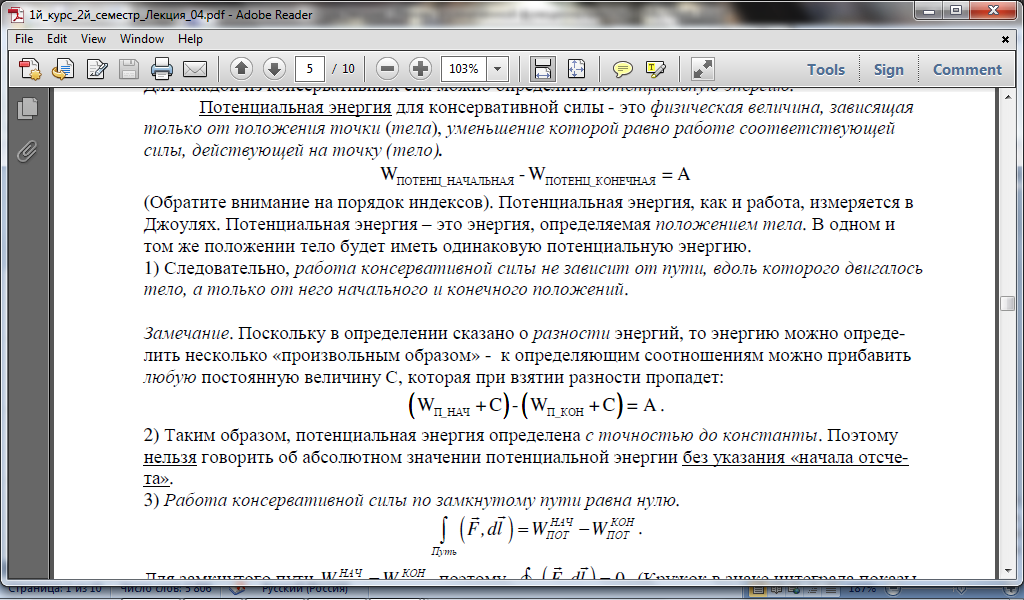
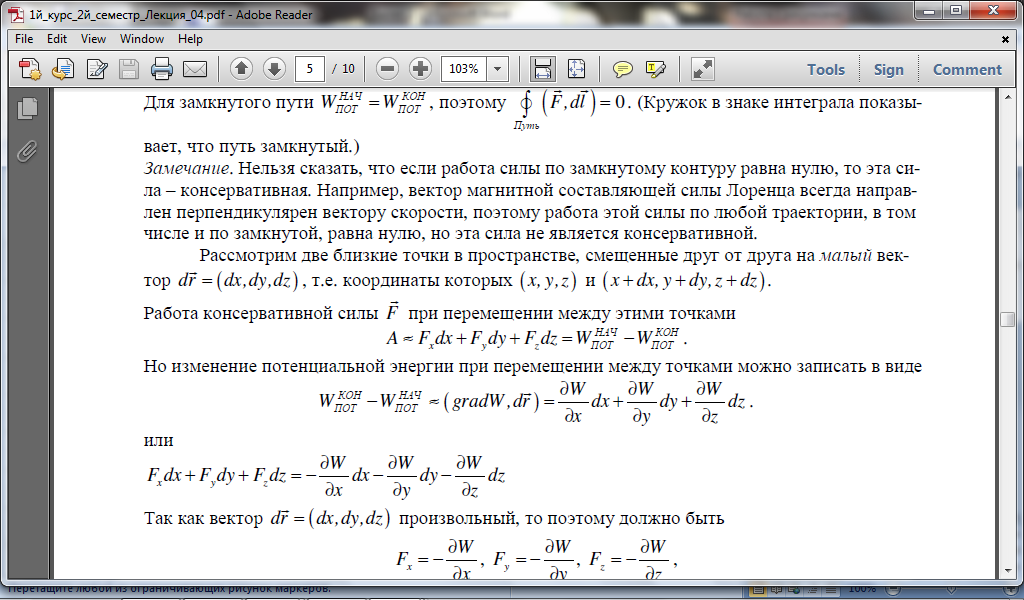
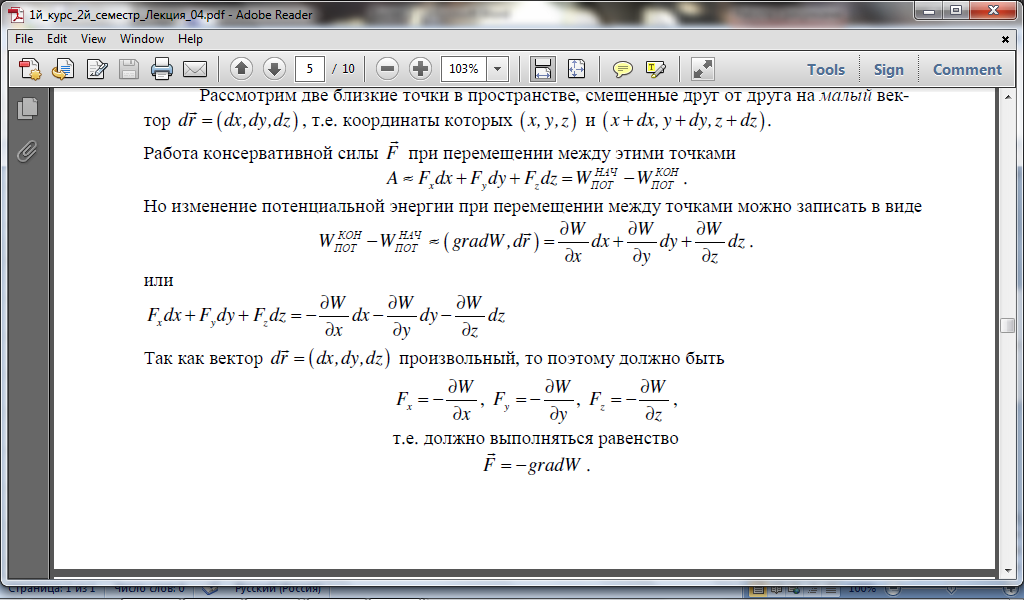
- •1. Связь между потенциальной энергией и силой. Потенциальная энергия тяготения и упругих деформаций.
- •1.Физический маятник. Квазиупругая сила.
- •2.Мощность.Единицы измерения в си.
- •Билет 22.
- •Гармгармонич2.Квазиупругая сила , имерение в си.
- •Билет 25.
Билет №1 Вопрос №1.
Основное уравнение динамики вращения твердого тела с неподвижной осью вращения:
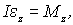 где
где 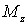 -
суммарный момент всех внешних сил
относительно оси вращения,
-
суммарный момент всех внешних сил
относительно оси вращения,
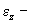 проекция
углового ускорения на ось вращения.
проекция
углового ускорения на ось вращения. Вычисление момента инерции тела проводится по формуле
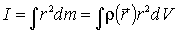
где dm и dV - масса и объем элемента тела,
находящегося на расстоянии ![]() от
интересующей нас оси z,
от
интересующей нас оси z, ![]() -
плотность тела в данной точке.
-
плотность тела в данной точке.
Вопрос №2.
Тангенциа́льное
ускоре́ние — компонента ускорения,
направленная по касательной к
траектории движения. Характеризует
изменение модуля скорости в отличие
от нормальной компоненты, характеризующей
изменение направления скорости
|
Билет №2 Вопрос №1.
Вопрос №2.
|
Билет №3
Вопрос №1.
Пусть
колебания заданы уравнениями:
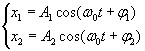 .
.
Тогда
результирующее имеет вид:
![]()
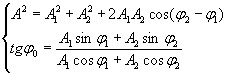
В зависимости от разности фаз (φ2-φ1): 1) (φ2-φ1) = ±2mπ (m=0, 1, 2, …), тогда A= А1+А2; 2) (φ2-φ1) = ±(2m+1)π (m=0, 1, 2, …), тогда A= |А1-А2|
П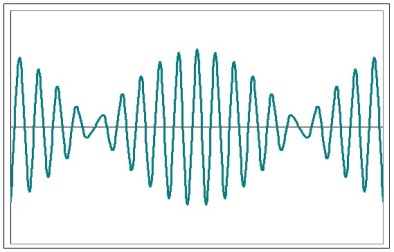 усть
усть
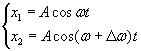 ,
тогда
,
тогда
![]() ,
Амплитуда изменяется по закону
,
Амплитуда изменяется по закону
![]() .
.
Вопрос №2.
Момент импульса материальной точки
относительно точки (полюса) O
определяется векторным произведением
![]() ,
где
,
где
![]() — радиус-вектор, проведенный из точки
O,
— радиус-вектор, проведенный из точки
O,
![]() — импульс материальной точки.
— импульс материальной точки.
Билет №4
Вопрос №1.
Работа переменной силы, действующей на тело, движущееся по криволинейной траектории
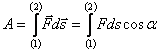 .
.
Приращение кинетической энергии материальной частицы равно суммарной работе всех сил, действующих на частицу:
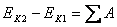
Вопрос №2.
Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси z.
При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса ri со скоростью vi . Скорость vi и импульс mi vi перпендикулярны этому радиусу, т. е. радиус является плечом вектора mi vi. Значит, мы можем записать, что момент импульса отдельной частицы равен
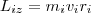 и направлен по оси в сторону, определяемую
правилом правого винта.
и направлен по оси в сторону, определяемую
правилом правого винта.

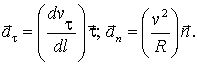 Измеряется в м/c2
Измеряется в м/c2