Высокий уровень

Задача В равнобедренную трапецию вписана окружность с радиусом 2 см. Найдите стороны трапеции, если ее площадь равна 20 см².

Задача Найдите наименьшую высоту треугольника со сторонами 13 см, 14см, 15 см.

Задача В прямоугольном треугольнике АВС из вершины прямого угла провели медиану СМ и высоту СН. Найдите гипотенузу, если СМ:СН = 5:4, а МН = 3 см.

Задача Диагонали трапеции равны 4 см и 3 см, а отрезок, который соединяет середины оснований – 2,5 см. Найдите площадь трапеции.

Задача Диагонали вписанного четырехугольника взаимно перпендикулярны. Докажите, что полусумма квадратов его сторон равна квадрату диаметра окружности.

IV. Этап использования

4.1. Включение теоремы в систему знаний

Прямоугольный треугольник

Катеты

Гипотенуза

Теорема Пифагора

4.2. Применение теоремы

Задача: Мальчик прошел от дома по направлению на восток 800 м. затем повернул на север и прошел 600 м. На каком расстоянии от дома оказался мальчик?

Решение: Так как расстояние – это гипотенуза прямоугольного треугольника, то оно равно по теореме Пифагора 1000 м.

Задача: Лестница длиной 12,5 м приставлена к стене так, что расстояние от ее нижнего конца до стены равно 3,5 м. На какой высоте от земли находится вершина лестницы?

Решение: По теореме Пифагора верхний конец лестницы будет находиться на расстоянии 12 м от земли.

Задача: Имеется бамбук высотой в 1 чжан. Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня (1 чжан = 10 чи).Какова высота бамбука после сгибания?

Решение: Решение: (10-x)²=x²-9; -20x=9-100, -20x=-109, x=109/20 чи. Ответ: x= 4,55 чи.

Задача: в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки 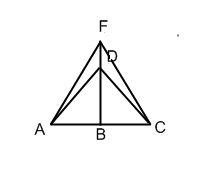AC=8 м., и AB=BF.

Решение:  Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда из треугольника DBC: DB=2,5 м., из треугольника АВF:  АF=√4²+4²=√32≈5,7 м.

Задача: Какую наименьшую высоту должна иметь вышка мобильной связи, поставленной в селе Утянка, чтобы село Ярки попало в зону связи (расстояние от вышки до Ярков по прямой 10 км. , радиус Земли равен 6380 км.)?

Решение: Применив теорему Пифагора, получу уравнение (х+6380)²=10²+6380²; х²+12760х-100=0; D=162817600+400=162818000; ≈12760,016; х≈0,008км.

З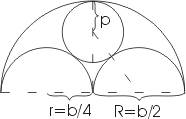 адача: Вычислите радиус меньшей окружности в конструкции рамы окна, внешняя часть которой имеет форму полукруга радиуса R

Решение: ).Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p. По теореме Пифагора имеем: (b/4+p)²=( b/4)²+( b/2-p)²; или b²/16+ bp/2+p²=b²/16+b²/4-bp+p²; откуда bp/2=b²/4-bp. Разделив на b и приводя подобные члены, получим: (3/2)p=b/4, p=b/6.