3. Анализ точности в установившемся режиме

Пусть система описывается дифференциальным уравнением .

В момент времени на вход системы поступает воздействие x(t) и система при этом в момент времени имеет ненулевые начальные условия (наличие в системе запасенной энергии, порожденной действием предыдущего сигнала, поступившего на систему до t = 0). Введем новые понятия.

Сигнал , порожденный входным воздействием , поступившим на систему в момент , называется вынужденным движением (вынужденными колебаниями) системы;

Сигнал , порожденный ненулевыми начальными условиями, называется свободным движением (свободными колебаниями) системы.

Выходной сигнал системы будет иметь вид: .

Изображение выходного сигнала с учётом правила дифференцирования оригинала при ненулевых начальных условиях будет иметь следующий вид:

.

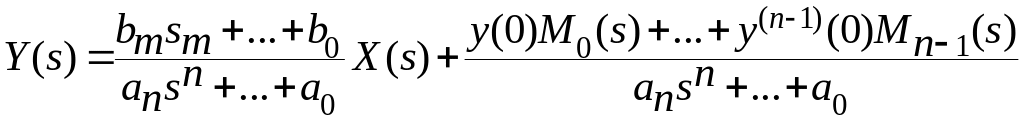Первое слагаемое учитывает влияние внешнего воздействия, второе слагаемое - эффект действия ненулевых начальных условий.

Рассмотрим вынужденный сигнал при нулевых начальных условиях и . Изображение выходного сигнала имеет вид:

.

Выходной сигнал, соответствующий , имеет вид:

,

где – корни уравнения А(s) = 0 (полюса системы);

– нулевой корень, порожденный воздействием .

Введем понятия установившегося (статического) и неустановившегося (динамического) режимов работы системы.

Составляющая порождена полюсом воздействия х(t)=1(t) и называется установившимся сигналом.

Составляющая порождена полюсами передаточной функции и называется переходным сигналом.

Эта составляющая определяет динамические свойства системы, т.к. с физической точки зрения порождена инерционностью системы.

Формулы для расчета имеют вид: , .

Т.о., вынужденный сигнал состоит из двух составляющих .

Режим, при котором составляющая отлична от нуля, называется неустановившимся или переходным (динамическим).

Режим, при котором , называется установившимся или статическим.

Т.о., выходной сигнал может быть записан , где

– сигнал, порожденный полюсами передаточной функции системы;

– сигнал, порожденный полюсами входного воздействия;

– сигнал, порожденный ненулевыми начальными условиями.

Рис. 7. Выходной сигнал системы при x(t) = 1(t)

Разность между входным и выходным сигналом называется ошибкой системы, т.е. .

Ошибка системы при условии, что и отличны от нуля, называется переходной или динамической.

Ошибка системы, определяемая формулой , при условии, что и стремятся к нулю, называется установившейся или статической.

Разность между максимальным отклонением при и статическим отклонением представляет собой динамическое отклонение.

Для определения ошибки в установившемся режиме необходимо уметь вычислять передаточные функции системы при поступлении на неё воздействий, разных по виду и месту воздействия.

Рассмотрим типовую одноконтурную систему управления, на которую поступает задающее воздействие, содержащее цель управления, и возмущение :

Определим передаточные функции системы для разных воздействий и приведём формулы упрощённого вычисления передаточных функций.

Передаточная функция прямой цепи по задающему воздействию при ( ).

1. Передаточная функция разомкнутой системы по при ( ).

,

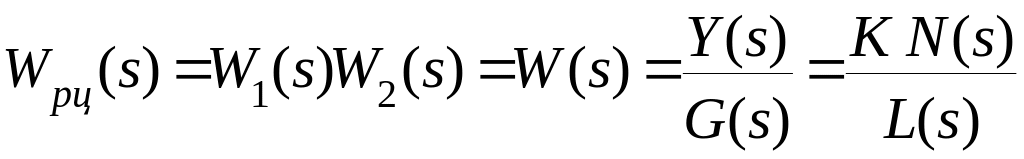где - общий коэффициент усиления,

- многочлены с единичными коэффициентами при младших членах.

2. Передаточная функция замкнутой системы по при ( ).

, где

3. Передаточная функция замкнутой системы по ошибке по задающему воздействию при ( ).

Передаточная функция прямой цепи по возмущению при ( )

4. Передаточная функция разомкнутой системы по возмущению при ( )

5. Передаточная функция замкнутой системы по возмущению при ( )

, где - многочлен зависит от места приложения возмущающего воздействия.

6. Передаточная функция замкнутой системы по ошибке по возмущению при ( ).

Для замкнутой системы изображение выходного сигнала имеет вид:

.
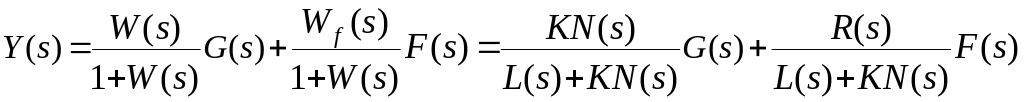