Вопрос8 Критерий выбора вида средней при экономических расчетах

Вопрос 9 абсолютные показатели вариации

Вариация – это изменение значения признака у отдельных единиц совокупности.

 (R). Размах вариации – это разность между наибольшим и наименьшим значением признака в изучаемой совокупности:

R=x_max – x_min,

Размах вариации не отражает отклонений всех значений признака – это его недостаток.

среднее линейное отклонение (d).- применяется для измерения отклонения каждой варианты от средней величины в ряду распределения или в группировке.

а) для несгруппированных данных (ранжировочного ряда)   (простое);

б) для вариационного интервального ряда:   (взве­шенное).

Среднее линейное отклонение показывает, на сколько в среднем каждое значение признака отклоняется от средней величины.

Средние линейные отклонения применяются на практике для анализа состава рабочих, ритмичности производства, равномерности поставок материалов и т.д.

дисперсия признака или средний квадрат отклонений, или квадрат среднего квадратического отклонения ( ). Дисперсия –   – определяется по формулам:

а) для ранжировочного ряда (несгруппировочных данных):  (простая);

б) для интервального ряда:   (взвешенная).

1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:

Или =

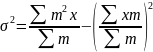
Корень квадратный из дисперсии   представляет среднее квадратическое отклонение ( ):  ; или

а) для ранжировочного ряда:   (простое);

б) для вариационного ряда:   (взвешенное).

Среднее квадратическое отклонение дает обобщенную характеристику признака совокупности и показывает во сколько раз в среднем колеблется величина признака совокупности.

Вопрос10 относительные показатели вариации

Для сравнения вариации в разных совокупностях рассчитываются относительные показатели вариации.

Коэффициент вариации – это отношение среднеквадратического отклонения к среднеарифметическому, рассчитывается в процентах:

.

Коэффициент вариации позволяет судить об однородности совокупности:

–   17% – абсолютно однородная;

–  17–33%% – достаточно однородная;

–  35–40%% – недостаточно однородная;

–  40–60%% – это говорит о большой колеблемости совокупности.

К оэффициентом осцилляции отражает относительную колеблемость крайних значений признака вокруг средней

.

Линейный коэффициент вариации характеризует долю усредненного значения абсолютного отклонения от средней величины.  .

Вопрос11 дисперсия альтернативного признака.

Альтернативный признак тот, который принимает 2 значения (Дихотомный признак) например: Да/нет

Признак оценивается ДОЛЕЙ «P» Пример: Доля домов с лифтами => доля домов без лифтов q=1-P

Пусть n – число единиц совокупности; m – число единиц совокупности, обладающих данным признаком; p – доля единиц, обладающих данным признаком (p=m/n); q - доля единиц, не обладающих данным признаком, причем p+q =1.  Альтернативный признак принимает всего два значения – 0 и 1 с весами соответственно q и p. Вычислим среднее значение альтернативного признака по формуле средней арифметической: 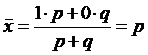 .  Дисперсия альтернативного признака определяется по формуле: 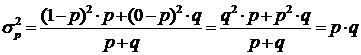 ,  где !Синтаксическая ошибка, R – среднеквадратическое отклонение альтернативного признака.  Вычислим дисперсию альтернативного признака по следующим данным: налоговой инспекций одного из районов города проверено 86 коммерческих киосков и в 37 обнаружены финансовые нарушения. Тогда    Следовательно, дисперсия и среднее квадратическое отклонение доли коммерческих киосков, имеющих финансовые нарушения, во всей совокупности обследованных киосков равны: