7 . Шум резистора

Если резистор сопротивлением R включен в электрическую цепь с полосой пропускания f и эта цепь не соединена с источником питания, то на выводах резистора существует переменное напряжение, имеющее вид случайных колебаний. Среднее значение этих колебаний равно 0, а средний квадрат напряжения определяется формулой Найквиста:

где k =1,3810^-23, , T – температура резистора, находящегося в тепловом равновесии с окружающей средой.

Это случайное напряжение обусловлено хаотическим движением подвижных носителей заряда – электронов в резисторе, в результате чего в каждый момент времени существует разность зарядов на концах резистора, а, следовательно, и напряжения. Хаотическое движение электронов существует при абсолютной температуре Т>0, и поэтому шум называется тепловым.

При анализе шумов электрических цепей шумящий резистор представляется в виде эквивалентной схемы, состоящей из источника случайного напряжения шума и нешумящего резистора.

Воспользовавшись формулой:

,

где - средний квадрат шумового тока, - проводимость резистора, запишем

В этом случае эквивалентную схему шумящего резистора можно представить в виде параллельного соединения генератора шумового тока и нешумящей проводимости G. Эквивалентные схемы шумящего резистора приведены на рис. 10.1.

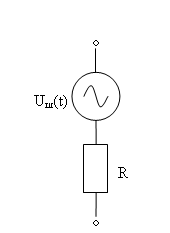
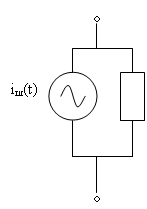
а)

б)

а – последовательная,

б – параллельная.

В колебательном контуре существуют потери, так что в его эквивалентную схему включают резисторы – рис. 10.2.

Рис. 10.2. Эквивалентная схема колебательного контура.

На этом рисунке r₁ и r₂ – сопротивления потерь в индуктивности и емкости контура. Импеданс контура:

jX, , (10.1)

- резонансное сопротивление контура,

,

,

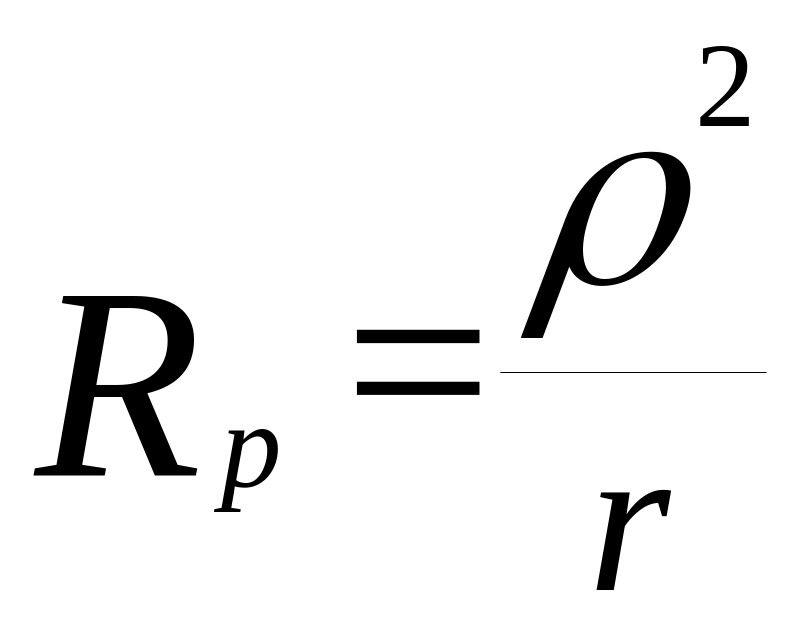- обобщенная расстройка.

Воспользовавшись формулой Найквиста в обобщенном виде

и подставив сюда выражение (10.1), получим формулу для расчета шума колебательного контура:

,

где - (10.2.)

шумовая полоса колебательного контура.

Обычно при анализе колебательного контура интегрируется частотами вблизи резонансной частоты, находящимися в полосе ее пропускания. Как известно, границы полосы пропускания соответствуют частотам, на которых а=1. Получим связь шумовой полосы контура с его полосой пропускания.

В этой целью в (10.2) заменим переменную f на a. Используя выражения для а, получим:

. =>

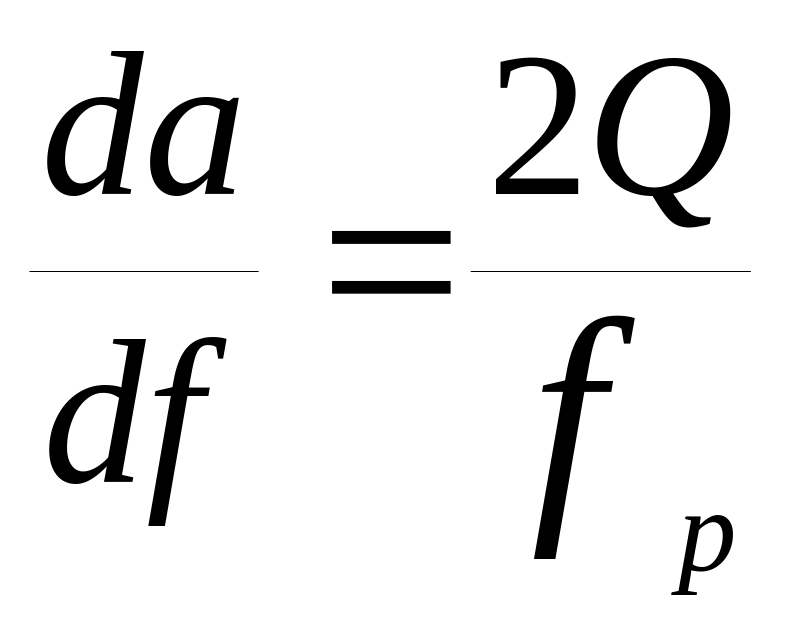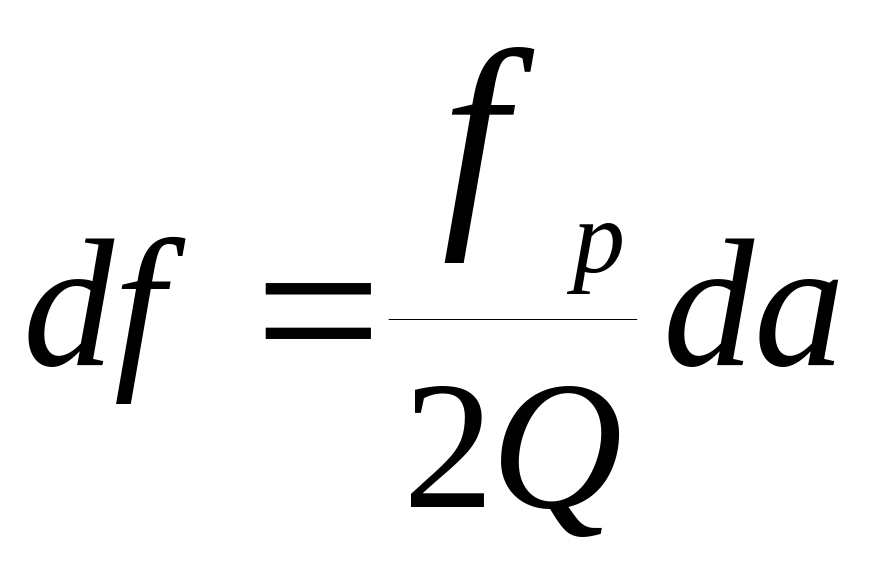
и возьмем интеграл (10.2.) в пределах от а₁=-2Q до а₂=

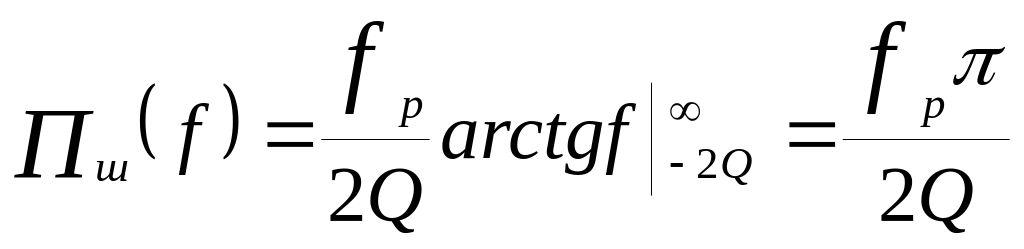
Так как полоса пропускания контура по уровню – 3дБ

то шумовая полоса контура

Таким образом, можно считать, что шумовая полоса контура приблизительно равна его полосе пропускания.

Коэффициент шума четырехполюсника

Допустим, на входе четырехполюсника имеется источник входного напряжения с внутренним сопротивлением R_ист – рис. 10.3.

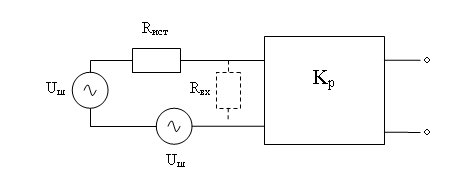
Рис. 10.3. Подключение источника колебаний к четырехполюснику.

Для максимальное передачи мощности от источника к четырехполюснику требуется, чтобы его входное сопротивление было равно внутреннему сопротивлению источника R_ист. В этом случае мощность шума, поступающего от сопротивления R_ист в четырехполюсник,

,

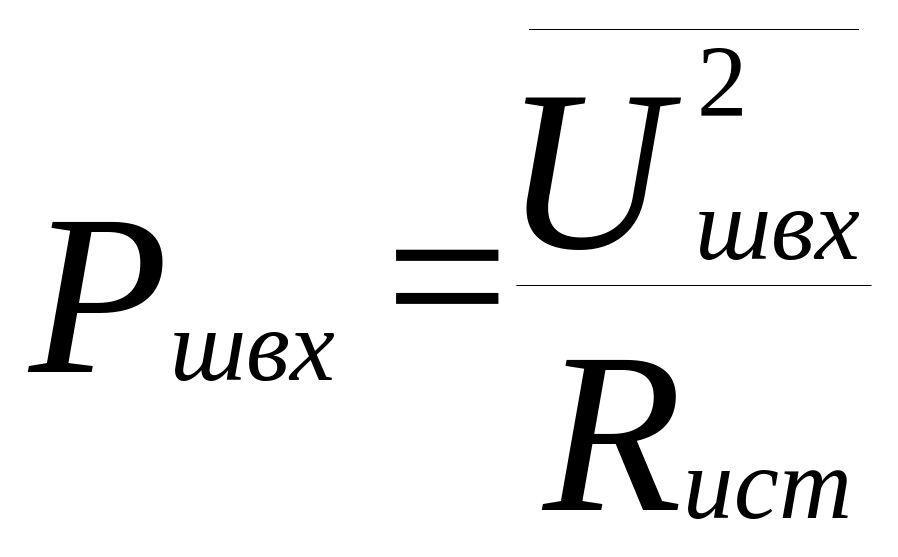где - средний квадрат шумового напряжения на входном сопротивлении ,

и мощность шума на входе четырехполюсника

(10.3.)

Если бы четырехполюсник был идеальным, нешумящим, то мощность шума на его выходе была бы равна , где – коэффициент передачи мощности. Реальный четырехполюсник добавляет к этому значению собственный шум мощности . Поэтому мощность шума на выходе четырехполюсника:

(10.4.)

Отношение мощности шума на выходе реального четырехполюсника к мощности выходного шума идеального, нешумящего, четырехполюсника называют коэффициентом шума N.

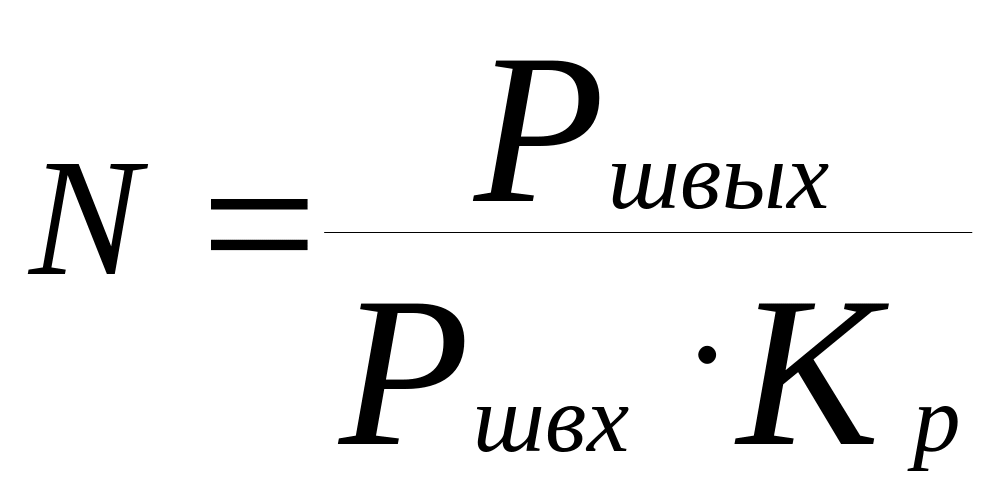(10.5.)

В радиоприемниках часто используют величину сигнал/шум, т.е. отношение мощности сигнала к мощности шума. В связи с этим, применяют другое определение коэффициента шума:

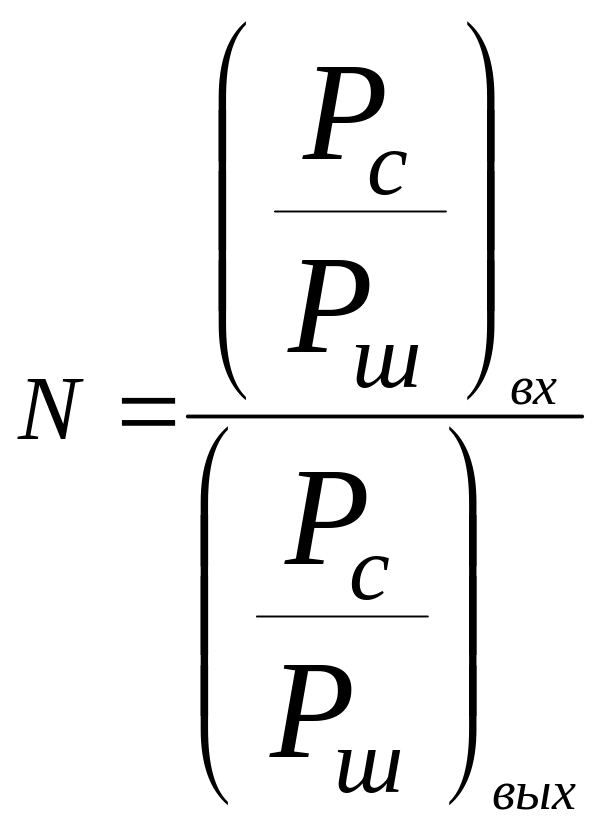(10.6)

Учитывая, что , легко показать, что определения коэффициента шума (10.5.) и (10.6.) равноценны. С использованием (10.4.) можем записать:

(10.7.)

Из (10.7.) видно, что коэффициент шума четырехполюсника всегда больше 1. Часто N выражают в децибеллах, при этом, всегда коэффициент шума в децибеллах:

10 lg N>0 дБ.

Шумовая температура приемной антенны.

Шумовые свойства антенны можно проанализировать, представляя ее последовательным включением двух сопротивлений – сопротивления излучения R_изл и сопротивлением тепловых потерь R_пот. Сопротивление излучения R_изл – это некоторый коэффициент пропорциональности между принимаемой мощностью и наведенным в приемной антенне напряжением амплитудой U_пр:

Шум сопротивления излучения определяется формулой Найквиста

,

где температура отличается от температуры окружающей среды Т и зависит от диаграммы направленности антенны и ее ориентации в пространстве. Например, если диаграмма направленности узкая, то становится меньше T, при ориентации луча антенны на Солнце становится больше Т.

Шум сопротивления потерь R_пот также определяется формулой Найквиста, куда следует поставить температуру окружающей среды.

Суммарный шум антенны:

Средний квадрат суммарного шумового напряжения можно представить в виде:

Суммарное сопротивление антенны:

Шум антенны может быть записан в виде:

,

Величина T_A – шумовая температура антенны.