Точки в бесконечности

Двумерный вектор однородных координат образует точку в бесконечности на линии

Для иллюстрации этого рассмотрим линию и точку, однородные координаты которой имеют вид , при .

Видно, что при . При этом все время сохраняется соотношение , то есть точка движется в бесконечность по указанной прямой. Из этого следует, например, что вектор однородных координат характеризует точку в бесконечности на оси абсцисс ; вектор – точку в бесконечности на оси ординат .

4) Трехмерные преобразования и проекции.

Процесс вывода трехмерной графической информации по сути своей является более сложным, чем соответствующий двумерный процесс. Это связано с тем, что экран ЭВМ–это плоскость, и в процессе визуализации трехмерная информация все равно должна быть преобразована в двумерную. Это осуществляется с помощью проекций. Рассмотрим сначала способы преобразования трехмерной информации. Точка в трехмерном пространстве с использованием однородных координат представится четырехмерным вектором или .

Преобразование однородных координат описывается соотношениями

;

,

где –матрица преобразования. Обобщенная матрица для трехмерных однородных координат имеет порядок и записывается как

Эта матрица может быть представлена как совокупность четырех частей:

Матрица

осуществляет покоординатное изменение масштаба, сдвиг и вращение; матрица – перенос

матрица – преобразования в перспективе;

матрица – общее изменение масштаба

Иногда преобразование матрицей размера для плоских однородных координат называется линейным. Соответственно, преобразование матрицей размера для трехмерных однородных координат называется билинейным.

Изменение масштаба

Покоординатное изменение масштаба выполняется с помощью диагональных элементов :

Сдвиг

За преобразование сдвига “отвечают” недиагональные элементы верхней левой подматрицы

Вращение вокруг координатных осей

В трехмерном случае вращение вокруг оси

то есть первая строка и первый столбец имеют вид

Вокругоси аналогично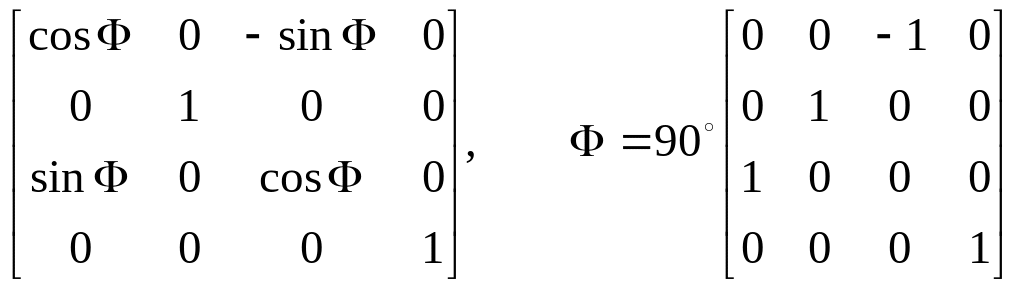 В

округ оси

Положительное направление определяется как направление против часовой стрелки, если смотреть вдоль оси, вокруг которой осуществляется вращение, к началу координат.

Отображение относительно координатных плоскостей

Отображение относительно плоскости меняет лишь знак координаты точек. Таким образом,

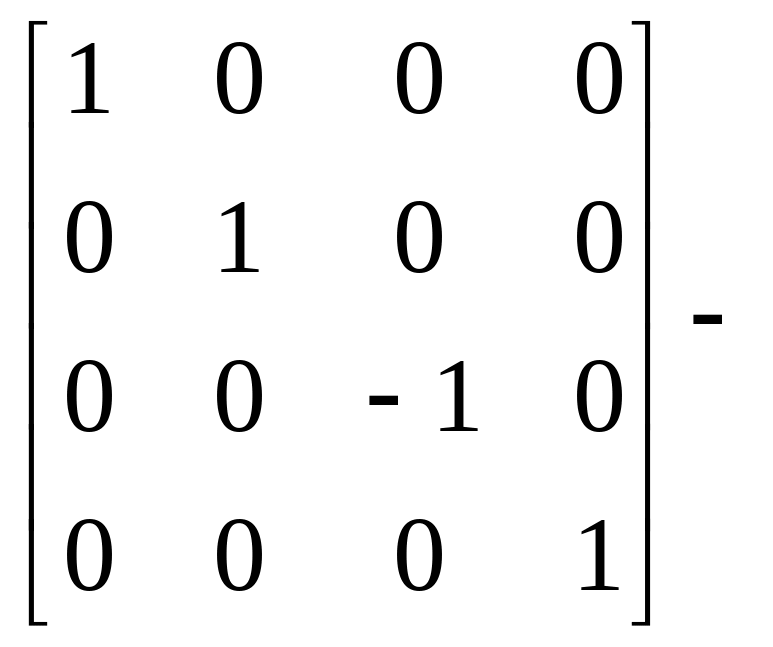отображение относительно

отображение относительно

Пространственный перенос

Трехмерный линейный перенос изображения определяется выражением:

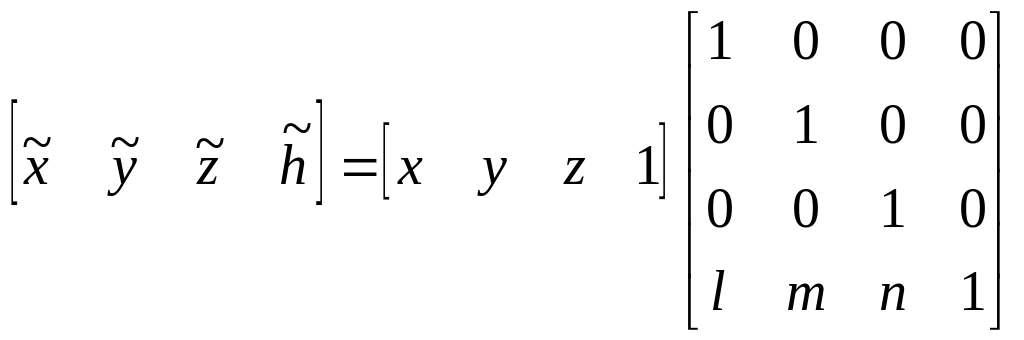
откуда

то есть

Трехмерное вращение вокруг произвольной оси

В трехмерном случае ставится задача вращения вокруг произвольной оси в трехмерном пространстве. Метод заключается в последовательном выполнении переноса, вращения вокруг оси, проходящей через начало координат и обратного переноса – переноса начала координат в исходное состояние

При этом ось вращения должна быть перпендикулярна плоскости .

При этом, однако, ось, проходящая через начало координат, может иметь произвольное направление.

Итак, если ось, вокруг которой выполняется вращение, проходит через точку , то матрица преобразования однородных координат определяется как