4.6. Расчет области устойчивости

Для построения границ области устойчивости для дискретных систем, порядок характеристического полинома которых выше третьего, рационально использовать критерий Михайлова. Для того, чтобы дискретная система была устойчива, необходимо и достаточно, чтобы при возрастании относительной частоты от 0 до π годограф характеристического уравнения

системы, начинаясь с положительной части действительной оси, последовательно обходил 2n квадрантов против часовой стрелки, нигде не обращаясь в нуль, где n- порядок характеристического уравнения системы.

Если характеристический полином замкнутой системы имеет вид:

(14)

то апериодическая граница устойчивости системы получается из уравнения при z=1, что соответствует .

Условие нахождения системы на колебательной границе устойчивости заключается в прохождении кривой Михайлова через начало координат. Тогда уравнение границы устойчивости получаем из (14) заменой и приравниванием к нулю вещественной и мнимой частей выражения. Формула Эйлера для относительной частоты принимает вид: , а для старших степеней переменной z - .

Для рассматриваемого примера характеристический полином найдем из выражения для передаточной функции замкнутой системы

.

Тогда выражения для границ области устойчивости примут вид:

для апериодической границы или ;

для колебательной границы

Отсюда и

.

Изменяя от 0 до π, получим область устойчивости в плоскости настроек регулятора k₁ и k₂ (рис.10). Из рисунка видно, что начальное значение относительной частоты отлично от 0. Это связано с тем, что при вычислении параметра k1 для рассматриваемого примера в знаменателе содержится и при появляется ошибка «Деление на 0».

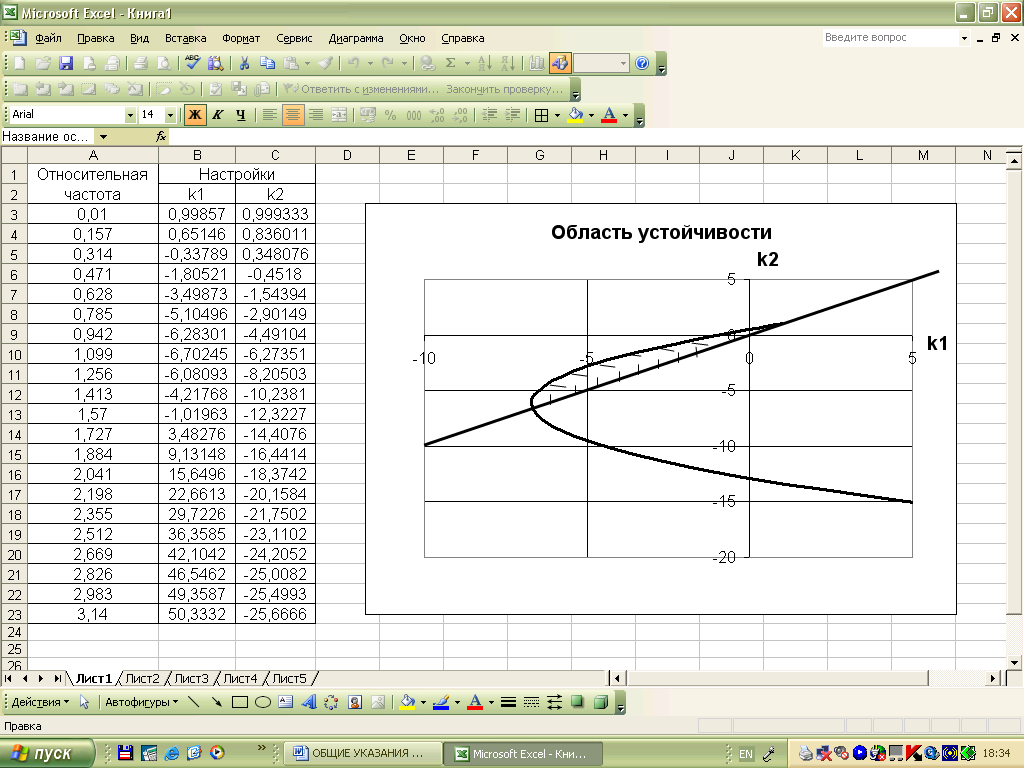
Рис.10 Фрагмент расчета области устойчивости замкнутой дискретной системы регулирования

4.7.Выбор оптимальных параметров управления

Устойчивость системы является, как правило, необходимым, но далеко не достаточным условием для того, чтобы система выполняла свое назначение. Возникает задача обеспечения не только устойчивости, но и надлежащего качества системы и, более того, наилучшего в том или ином смысле режима функционирования. Такая задача может быть названа задачей оптимизации. В качестве критерия оптимальности могут быть приняты различные технические и технико-экономические показатели (производительность, расходы технологических и энергетических ресурсов, показатели технологического процесса и т.д.) В данной курсовой работе критерии качества системы определяются в задании. Они могут быть сформулированы, например, в виде следующих показателей качества ее работы:

• точность работы системы в установившемся режиме не должна быть меньше заданной;

• система должна иметь заданный запас устойчивости;

• время регулирования не должно превышать заданной значение или должно быть минимальным.

В качестве критерия оценки запаса устойчивости используются различные показатели и методы. Наиболее распространенными численными показателями запаса устойчивости являются:

• запасы по фазе φ_з, по модулю L₁, L₂ и показатель колебательности М, определяемые с использованием частотных методов исследования;

• степень колебательности m, определяемая с использованием корневых методов исследования.

В этой части методических указаний рассмотрим вопрос выбора области параметров системы, обеспечивающих заданный запас устойчивости в виде степени колебательности m.

Степень колебательности m характеризует скорость затухания колебательных составляющих переходного процесса, определяетмых комплексными корнями характеристического уравнения вида

и определяется как

, .

Задание степени колебательности ограничивает область расположения корней характеристического уравнения системы на плоскости корней p двумя лучами ОА и ОВ, которые составляют с вещественной осью угол, равный (рис. 11, а). На практике вместо понятия степень колебательности часто применяют понятие степень затухания, которая определяется по соотношению между амплитудами колебаний переходного процесса y(t)(рис.11, б) и часто выражается в процентах

.

Рис. 11 Определение запаса устойчивости системы по степени колебательности

Рис.12 Определение запаса устойчивости системы по степени затухания

При синтезе системы на заданную степень колебательности m или степень затухания Ψ необходимо, чтобы пара ближайших к мнимой оси комплексно-сопряженных корней и характеристического уравнения замкнутой системы регулирования была расположена на лучах ОА и ОВ. Обеспечивается это соответствующим выбором параметров системы, чаще всего регулятора. Прямой метод подбора параметров и анализ расположения корней трудоемок. Удобнее производить расчет системы на заданную степень колебательности с помощью метода расширенных АФЧХ.

Расширенная АФЧХ определяет свойства звена или системы в частотной области при подаче на вход периодического возмущения в виде

.

Процесс получения расширенных АФЧХ для дискретных систем является аналогичным такому же процессу для непрерывных систем. Последовательность действий по выбору оптимальных параметров СУ по заданному запасу устойчивости и минимуму дисперсии отклонения регулируемой величины от заданного постоянного значения такая же как и для непрерывных систем [1].

1. Находят выражения расширенных АФЧХ для непрерывной приведенной части системы и дискретного регулятора из соответствующих нормальных АФЧХ заменой z на .

2. Для определения границы с заданной степенью колебательности m в плоскости варьируемых параметров используют критерий Найквиста в виде выражения:

, (15)

что равносильно соблюдению следующих равенств

(16)

Если уравнение регулятора записывается со знаком «минус», то условие (15) запишется как

(17)

или

(18)

3. На полученной границе с заданным значением m выбираются конкретные значения варьируемых параметров (например, настроек регулятора).

Следующим этапом является выбор конкретных значений k₁ и k₂ на линии равного затухания. Кривые переходных процессов рассматриваемой системы по задающему воздействию приведены на рис.14.

Анализ переходных процессов, соответствующих разным значениям k₁ и k₂, лежащим на одной кривой, показывает, что качество процесса при заданной степени колебательности изменяется в зависимости от выбранных значений k₁ и k₂ .

Так, если двигаться по кривой при m=0,8 от меньших значений относительной частоты к большим, то сначала амплитуда колебаний регулируемой величины увеличивается (рис.14, кривые 1,2,3), затем амплитуда колебаний начинает уменьшатся с одновременным уменьшением времени переходного процесса (рис.14, кривые 4,5). При дальнейшем движении по кривой переходный процесс «затягивается» и система начинает характеризоваться остаточной неравномерностью (кривая 6).

Рис.14 Кривые переходных процессов дискретной системы управления

В результате рассмотрение этих кривых можно признать близким к оптимальному процесс, соответствующий кривой 5, при этом отсутствует остаточная неравномерность, длительность переходного процесса минимальна, а перерегулирование – в допустимых пределах.

Оптимальные настройки, соответствующие минимуму дисперсии регулируемого параметра, определяются на линии равной степени затухания при движении по ней в сторону увеличения относительной частоты за ее максимумом.