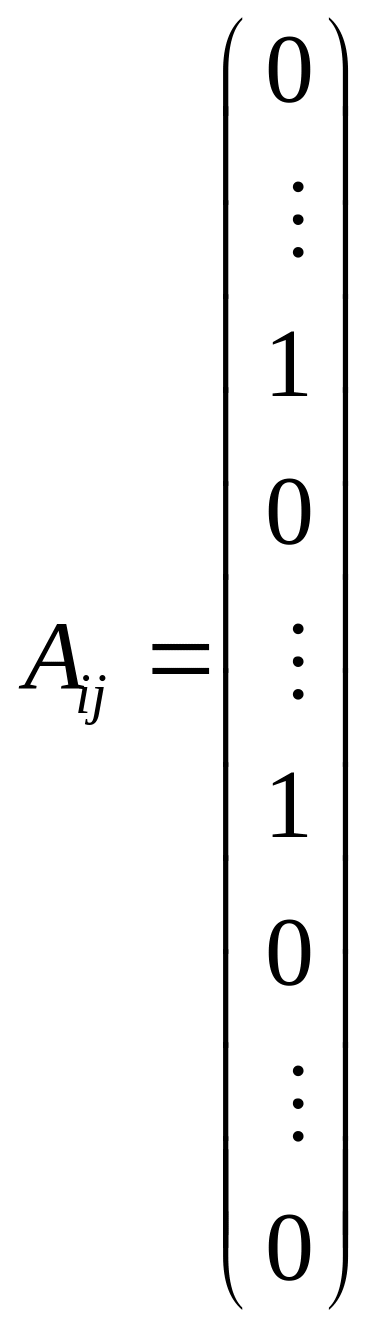- •Глава 3. Спеціальні задачі лінійного програмування та методи їх розв’язування
- •3.1. Транспортна задача
- •3.1.1. Постановка та математична модель транспортної задачі
- •3.1.2. Розв’язування транспортної задачі
- •3.2. Задача про призначення
- •3.3. Динамічне програмування
- •3.3.1. Вступ до динамічного програмування
- •3.3.2. Рекурентні співвідношення динамічного програмування
- •3.3.3. Обчислювальний алгоритм
- •3.3.4. Метод динамічного програмування за наявності двох обмежень
- •3.3.5. Задача про заміну обладнання
- •3.4. Задачі лінійного програмування великої розмірності
- •3.4.1. Характеристика підходів до розв’язування задач великої розмірності
- •3.4.2. Метод декомпозиції Данцига-Вульфа
- •3.5. Перевір себе
- •3.5.1. Контрольні запитання
- •3.5.2 Завдання та приклади для самостійної роботи
Глава 3. Спеціальні задачі лінійного програмування та методи їх розв’язування
3.1. Транспортна задача
3.1.1. Постановка та математична модель транспортної задачі
Серед задач лінійного програмування можна виділити деякі види задач, моделі яких мають певну специфіку. Прикладом такої задачі є, так звана, транспортна задача.
Постановка транспортної задачі пов’язана з визначенням такого плану перевезення вантажу від постачальників до споживачів, щоб загальні транспортні витрати були найменшими, за умов що мають бути задоволені потреби споживачів. Можливості кожного постачальника, а також потреби кожного споживача вважаються відомими.
Для
побудови економіко-математичної моделі
транспортної задачі введемо позначення:
![]() -
кількість постачальників;
-
кількість постачальників;
![]() -
номер постачальника,
-
номер постачальника,
![]() ;
;
![]() -
кількість вантажу у
-го
постачальника,
;
-
кількість вантажу у
-го
постачальника,
;
![]() -
кількість споживачів;
-
кількість споживачів;
![]() -
номер споживача,
-
номер споживача,
![]() ;
;
![]() -
потреби
-го
споживача;
-
потреби
-го
споживача;
![]() ;
;
![]() -
вартість перевезення одиниці вантажу
від
-
вартість перевезення одиниці вантажу
від
![]() -го
постачальника до
-го
споживача;
-го
постачальника до
-го
споживача;
![]() .
Невідомі моделі
.
Невідомі моделі
![]() ,
означають кількість вантажу, який
перевозиться від
-го
постачальника до
-го
споживача.
,
означають кількість вантажу, який
перевозиться від
-го
постачальника до
-го
споживача.
Загальні
транспортні витрати
![]() обчислюються за формулою:
обчислюються за формулою:
![]() .
.
Згідно з критерієм оптимальності ці витрати мають бути мінімальними, тому цільова функція транспортної задачі прямує до мінімуму:
|
(3.1.1) |
План
перевезень
![]() має задовольняти умовам:
має задовольняти умовам:
загальний обсяг вантажу, який вивозиться від кожного постачальника, не повинен
перевищувати його запасу:
|
(3.1.2) |
- обсяг вантажу, який надходить кожному споживачеві, не повинен бути менше від його
потреб:
|
(3.1.3) |
- обсяги вантажу на кожному з маршрутів повинні бути невід’ємними:
|
(3.1.4) |
Система умов (3.1.1) - (3.1.4) є математичною моделлю транспортної задачі.
Приклад
3.1.
Три пекарні
![]() та
та
![]() поставляють хлібобулочні вироби до
чотирьох магазинів
поставляють хлібобулочні вироби до
чотирьох магазинів
![]() та
та
![]() .
Добові потужності пекарень відповідно
складають 100 кг, 150 кг та 120 кг виробів.
Попит на хлібобулочні вироби у магазині
.
Добові потужності пекарень відповідно
складають 100 кг, 150 кг та 120 кг виробів.
Попит на хлібобулочні вироби у магазині
![]() не перевищує 130 кг, у магазині
не перевищує 130 кг, у магазині
![]() — 80 кг, у магазині
— 80 кг, у магазині
![]() — 100 кг, а у магазині
— 100 кг, а у магазині
![]() — 60 кг за добу. Транспортні витрати за
доставку одного кілограму виробів від
пекарень до магазинів наведені у таблиці
3.1.
— 60 кг за добу. Транспортні витрати за
доставку одного кілограму виробів від
пекарень до магазинів наведені у таблиці
3.1.
Таблиця 3.1.
|
|
|
|
|
|
3 |
2 |
5 |
4 |
|
5 |
6 |
2 |
1 |
|
7 |
9 |
10 |
12 |
Побудуємо математичну модель визначення оптимального плану доставки хлібобулочних виробів.
Змінні
моделі
![]() ,
будуть означати величину поставки
виробів з
-ої
пекарні до
-го
магазину. Критерій оптимальності плану
поставок визначається витратами, які
мінімізуються:
,
будуть означати величину поставки
виробів з
-ої
пекарні до
-го
магазину. Критерій оптимальності плану
поставок визначається витратами, які
мінімізуються:
![]()
![]() ,
,
за умов:
загальна величина поставок хлібобулочних виробів з кожної пекарні у різні
магазини не може перевищувати її потужності, тобто
![]() ,
,
![]() ,
,
![]() ;
;
кількість виробів, що завозяться до кожного магазину, не повинна бути меншою за
відповідний попит, тобто
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
- величини поставок продукції не можуть бути від’ємними
![]() .
.
Якщо
загальна пропозиція дорівнює загальним
потребам, тобто
![]() ,
тоді транспортна задача є збалансованою
(закритою). В цьому випадку
математична модель транспортної задачі
має вигляд:
,
тоді транспортна задача є збалансованою
(закритою). В цьому випадку
математична модель транспортної задачі
має вигляд:
|
(3.1.5) |
|
(3.1.6) |
|
(3.1.7) |
|
(3.1.8) |
Оскільки попит в усіх магазинах (130+80+100+60=370) дорівнює виробничим потужностям усіх трьох пекарень (100+150+120=370), тоді приклад 3.1. — приклад збалансованої транспортної задачі. Її модель можна записати у вигляді:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Теорема 3.1.1. Будь-яка збалансована транспортна задача є розв’язуваною задачею.
Доведення. Розглянемо матрицю , де
|
(3.1.9) |
По-перше,
покажемо, що
![]() є допустимим розв’язком задачі (3.1.5) -
(3.1.8). Невід’ємність величин
є допустимим розв’язком задачі (3.1.5) -
(3.1.8). Невід’ємність величин
![]() випливає з їх економічної інтерпретації,
а значить виконується умова (3.1.8) про
невід’ємність змінних транспортної
задачі. Підставимо вираз для
випливає з їх економічної інтерпретації,
а значить виконується умова (3.1.8) про
невід’ємність змінних транспортної
задачі. Підставимо вираз для
![]() в обмеження задачі (3.1.6) ті (3.1.8):
в обмеження задачі (3.1.6) ті (3.1.8):
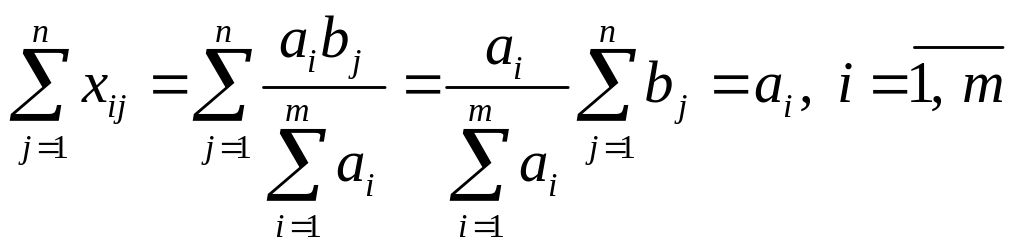 ;
;
 .
.
Змінні
![]() ,
визначені за формулою (3.1.9), задовольняють
обмеженням задачі, тобто існування
допустимих розв’язків транспортної
задачі доведено.
,
визначені за формулою (3.1.9), задовольняють
обмеженням задачі, тобто існування
допустимих розв’язків транспортної
задачі доведено.
По-друге, існування оптимального розв’язку транспортної задачі випливає з обмеженості допустимого многогранника. Дійсно,
![]() .
.
Теорему доведено.
При розв’язуванні реальних прикладних задач можливі ситуації, коли загальні потреби не дорівнюють загальним пропозиціям. Така транспортна задача називається незбалансованою. Щоб розв’язати таку транспортну задачу, треба спочатку звести її до збалансованої. Можливі дві ситуації:
1. Загальні потреби споживачів більші від загальної пропозиції постачальників:
![]() .
.
У такому разі транспортна задача нерозв’язувана через наявність дефіциту продукції у постачальників у кількості
![]() .
.
Постає
задача оптимізації перевезення наявної
кількості продукції. Для розв’язування
такої задачі необхідно ввести фіктивного
постачальника, який забезпечує
![]() одиниць продукції. Фіктивні поставки
продукції
одиниць продукції. Фіктивні поставки
продукції
![]() ,
означають дефіцит продукції у
,
означають дефіцит продукції у
![]() -го
споживача.
-го
споживача.
2. Загальні пропозиції постачальників більші від загальної потреби споживачів:
![]() .
.
У такому разі у постачальників залишається невивезеною продукція. Для розв’язування такої задачі необхідно ввести до неї фіктивного споживача, потреби у продукції якого дорівнюють
![]() .
.
Фіктивні
поставки продукції
![]() ,
означають залишок продукції в
-го
постачальника.
,
означають залишок продукції в
-го
постачальника.
І в
першій, і в другій ситуації нормативи
витрат на доставку продукції від
фіктивного постачальника
![]() ,
а також до фіктивного споживача
,
а також до фіктивного споживача
![]() ,
дорівнюють нулю.
,
дорівнюють нулю.
Математична модель транспортної задачі (3.1.5) – (3.1.8) є задачею лінійного програмування. Специфіка цієї задачі пов’язана з системою її обмежень. У розгорнутому вигляді система обмежень збалансованої транспортної задачі має вигляд:
|
(3.1.10) |
Умови
(3.1.10) — система (![]() )
лінійних рівнянь відносно (
)
лінійних рівнянь відносно (![]() )
змінних
.
По-перше, кожне рівняння цієї системи
є лінійною комбінацією решти рівнянь.
Наприклад, якщо додати (
)
змінних
.
По-перше, кожне рівняння цієї системи
є лінійною комбінацією решти рівнянь.
Наприклад, якщо додати (![]() )-е,
(
)-е,
(![]() )-е,
... та (
)-е
рівняння, а потім відняти з отриманої
суми 2-е, 3-є, ... та
-е
рівняння – дістанемо перше. Аналогічно
можна отримати будь-яке рівняння системи,
використовуючи інші рівняння. Таким
чином, система (3.1.10) містить (
)-е,
... та (
)-е
рівняння, а потім відняти з отриманої
суми 2-е, 3-є, ... та
-е
рівняння – дістанемо перше. Аналогічно
можна отримати будь-яке рівняння системи,
використовуючи інші рівняння. Таким
чином, система (3.1.10) містить (![]() )
лінійно незалежних рівнянь. Тому базис
цієї системи складається з (
)
лінійно незалежних векторів і кількість
базисних маршрутів
для будь-якої транспортної задачі
дорівнює (
).
)
лінійно незалежних рівнянь. Тому базис
цієї системи складається з (
)
лінійно незалежних векторів і кількість
базисних маршрутів
для будь-якої транспортної задачі
дорівнює (
).
По-друге,
кожна змінна
входить до системи обмежень (3.1.10) тільки
двічі — у
-те
та (![]() )-те
рівняння, причому щоразу з коефіцієнтом
1. Позначимо (
)-вимірний
вектор, складений з коефіцієнтів при
змінній
в обмеженнях транспортної задачі, через
)-те
рівняння, причому щоразу з коефіцієнтом
1. Позначимо (
)-вимірний
вектор, складений з коефіцієнтів при
змінній
в обмеженнях транспортної задачі, через
![]() .
Тоді структура цього вектора буде
наступною:
.
Тоді структура цього вектора буде
наступною:
|
- -е місце - ( )-е місце |
|
Для розв’язування транспортної задачі можна використовувати загальний метод лінійного програмування - симплекс-метод, але, враховуючи специфіку її математичної моделі, розроблено більш економний алгоритм, спеціально для транспортної задачі - метод потенціалів.

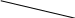 Магазини
Пекарні
Магазини
Пекарні .
.