13. Тепловое подобие.

Аналитическую зависимость между параметрами, определяющими значение коэффициента теплоотдачи, получить невозможно, поэтому на помощь привлекается эксперимент и теория подобия.

(1)

Уравнение, характеризующее условия теплообмена на границе раздела движущейся среды и твёрдого тела, имеет вид:

(2)

Точное решение дифференциальных уравнений (2) и (3) возможно лишь в редких случаях. Поэтому из данных уравнений методом теории подобия выводятся критерии подобия, и конвективный теплообмен представляется обобщённым уравнением в форме зависимости между критериями подобия. Эта зависимость имеет вид: Nu = f(Re, Pr, Gr, l/l_o … l_n/l_o), (4)

где Nu = al/l, критерий Нуссельта Nu характеризует отношение суммарного переноса теплоты конвекцией и теплопроводностью (т.е. теплоотдачей) к теплоте, передаваемой теплопроводностью (l – определяющий геометрический размер: например, для потоков, движущихся в трубе, - диаметр трубы) .

Re = wdr/m, критерий Рейнольдса Re, характеризует режим течения жидкости или газа или отношение сил трения к инерционным силам.

Pr = mc/l, критерий Прандтля Pr, характеризует подобие физических свойств теплоносителей и выражает меру отношения переноса импульса посредством внутреннего трения к переносу тепла посредством теплопроводности.

Gr = glr²bDt/m, критерий Грасгофа Gr, показывает отношение сил вязкости к произведению подъёмной силы, определяемой разностью плотностей в различных точках неизотермического потока и силы инерции. Он характеризует движение при естественной конвекции

где b - коэффициент объёмного расширения, град^-1

l – геометрический размер, м

Dt – разность температур между теплопередающей поверхностью и

жидкостью или газом, град

C – теплоёмкость потока, Дж/(кг×град).

При вынужденном движении жидкости (принудительная конвекция) уравнение (4) имеет вид:

Nu = с Re^m Prⁿ (l/d)^R или Nu = f₁(Re, Pr, l/l_o … l_n/l_o)

где m, n, k, c – величины, определяемые из опытов.

При естественной конвекции уравнение (4) может быть представлено в виде

Nu = с Gr^m Prⁿ (l/d)^R или Nu = f₂(Gr, Pr, l/l_o … l_n/l_o)

14. Теплопередача при стационарном режиме. Теплопередача через плоскую стенку.

Теплопередачей называется теплообмен между двумя средами через разделяющую их перегородку. Теплопередача является сложным видом теплообмена, в котором участвуют две среды и тело. Кроме того, в нём действуют одновременно и совместно все элементарные явления переноса теплоты (теплопроводность, конвекция, лучеиспускание).Количество переданной теплоты теплопередачей при стационарном режиме определяется по основному уравнению теплопередачи:Q = K×F×Dt, Вт,где Q – количество переданной теплоты, Вт. Dt – t_г – t_х, ^оС. t_г – температура горячего теплоносителя, ^оС, t_х – температура холодного теплоносителя, ^оС;F – теплообменная поверхность, м²,K – коэффициент теплопередачи, размерность которого получается из основного уравнения:[K] = [Q/FDt] = [Вт/м² × град] Коэффициент теплопередачи представляет собой количество теплоты, переданной через единицу поверхности в единицу времени от одного теплоносителя к другому при разности температур между ними в один градус. Коэффициент теплопередачи связывает между собой коэффициент теплопроводности и теплоотдачи.Рассмотрим случай, когда две среды разной температуры разделены однородной плоской стенкой. Коэффициент теплопроводности стенки - l и толщина её - d. Температура - t_C1 и t_C2, причём t_C1 > t_C2. Температура поверхностей стенки неизвестны, обозначим их как t_n1 и t_n2. Суммарный коэффициент теплоотдачи со стороны горячего теплоносителя равен a₁, а со стороны холодного - a₂По условию задачи температурное поле одномерно, режим стационарный. В этом случае вся теплота, переданная от горячего теплоносителя к поверхности стенки, проходит сквозь стенку и отдаётся холодному теплоносителю, т.е. указанные количества теплоты равны между собой.

Следовательно, для теплового потока q, где q = Q/Ft, можно написать систему из трёх уравнений:

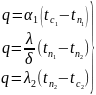
Из уравнений (1) находятся частные температурные напоры:

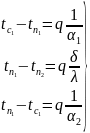
После сложения левых и правых частей уравнений (2) получается выражение для полного температурного напора t_C1 - t_C2 = q(1/a₁ + d/l + 1/a₂), (3)  откуда определяется значение удельного теплового потока:

Согласно формуле (4), тепловой поток прямо пропорционален разности температур между двумя теплоносителями и обратно пропорционален сумме термических сопротивлений.Вводя обозначение: К = 1/(1/a₁ + d/l + 1/a₂) в выражение (4), получим:q = K(t_C1 - t_C2) 

Величина К называется коэффициентом теплопередачи. Он устанавливает связь между элементарными видами теплообмена через коэффициенты теплоотдачи и коэффициенты теплопроводности.Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи:1/K = 1/a₁ + d/l + 1/a₂ , [м²×град/Вт] где d/l - термическое сопротивление стенки 1/a₁ и 1/a₂ - являются термическими сопротивлениями теплоотдачи от горячего теплоносителя к холодному.