Вариант 10
1. Вычислить неопределенные интегралы:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
.2. Вычислить определенные интегралы:
а)
|
б)
|
в)
|
.3. Пяти полевым радиостанциям разрешено во время учений работать на 6 радиоволнах. Выбор волны на каждой станции производится наудачу. Найти вероятность того, что будут использованы различные радиоволны.
4. Девушка забыла последнюю цифру номера телефона своего жениха и набрала ее наугад. Определить вероятность того, что ей придется набирать номер не более трех раз.
5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.
а) Вероятность появления некоторого события в каждом из 5 независимых опытов равна 0,2. Определить вероятность появления этого события по крайней мере 3 раза.
б) Всхожесть семян данного сорта растений составляет 90%. Найти вероятность того, что из 900 посаженых семян число проросших будет: 1) равно 800, 2) заключено между 805 и 820.
6. Дискретная случайная величина Х имеет только два возможных значения: x1 и x2, причем x1 < x2. Вероятность того, что Х примет значение x1 равно 0,3. Найти закон распределения Х, зная математическое ожидание М[X] = 2,7 и дисперсию D[X] = 0,21.
7. Непрерывная случайная величина Х задана функцией распределения
Найти: а) параметр k; б) математическое ожидание; в) дисперсию.
8. Известны математическое ожидание а=9 и среднее квадратичное отклонение =4 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (2, 10); б) отклонения этой величины от математического ожидания не более, чем на .
Вариант 11
1. Вычислить неопределенные интегралы:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
.2. Вычислить определенные интегралы:
а)
|
б)
|
в)
|
.3. На каждой из шести одинаковых карточек напечатана одна из следующих букв: а, т, м, р, с, о. Карточки тщательно перемешаны. Найти вероятность того, что на четырех, вынутых по одной и расположенных "в одну линию" карточках, можно будет прочесть слово "трос".
4. Вероятность брака из-за нарушения режима обработки деталей равна 0,02, а вследствие неисправности станка – 0,08. Какова вероятность выпуска бракованных деталей?
5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.
а) Вероятность хотя бы одного попадания стрелком в цель при 4 выстрелах равна 0,9919. Найти вероятность попадания в цель при одном выстреле, если вероятность попадания в цель при одном выстреле.
б) Посажено 600 семян кукурузы с вероятностью 0,9 прорастания для каждого семени. Найти вероятность того, что взойдет: 1) ровно 550 семян, 2) больше 535 и меньше 555.
6. Дискретная случайная величина Х имеет только два возможных значения: x1 и x2, причем x1 < x2. Вероятность того, что Х примет значение x1 равно 0,2. Найти закон распределения Х, зная математическое ожидание М[X] = 2 и дисперсию D[X] = 4.
7. Непрерывная случайная величина Х задана функцией распределения
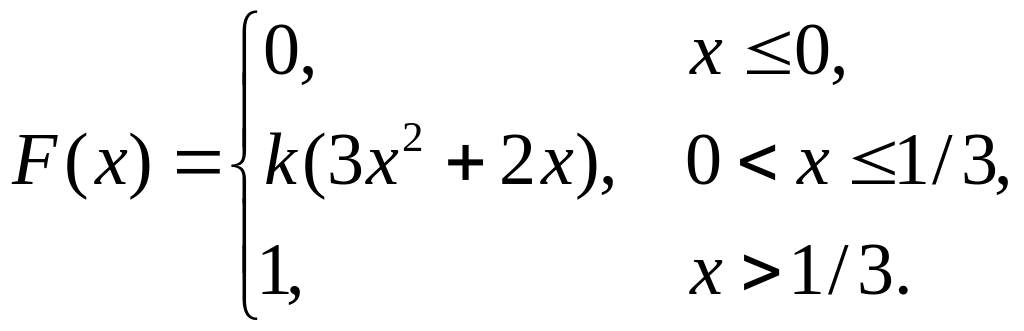
Найти: а) параметр k; б) математическое ожидание; в) дисперсию.
8. Известны математическое ожидание а=8 и среднее квадратичное отклонение =3 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (3, 5); б) отклонения этой величины от математического ожидания не более, чем на .
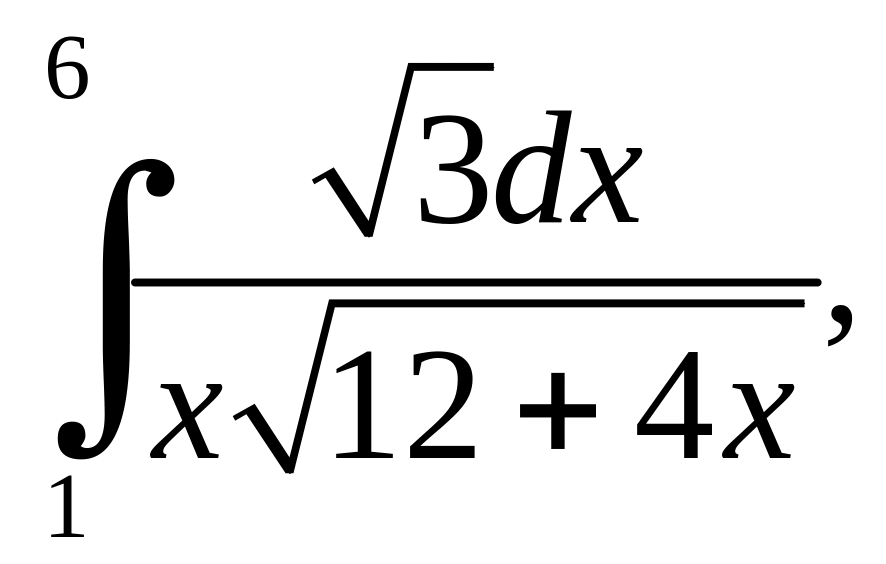
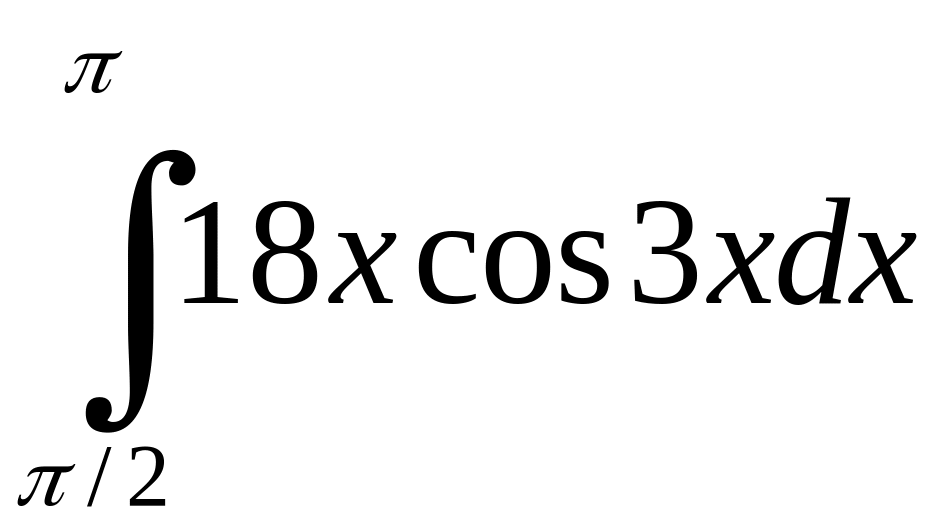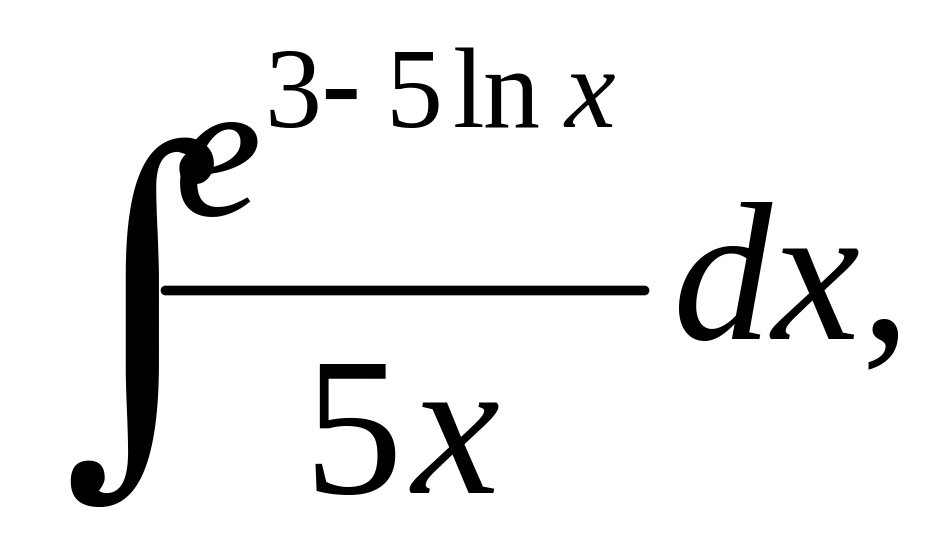
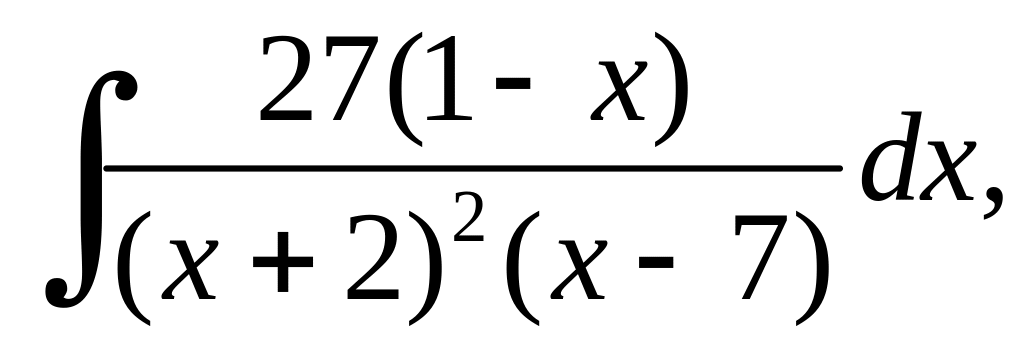
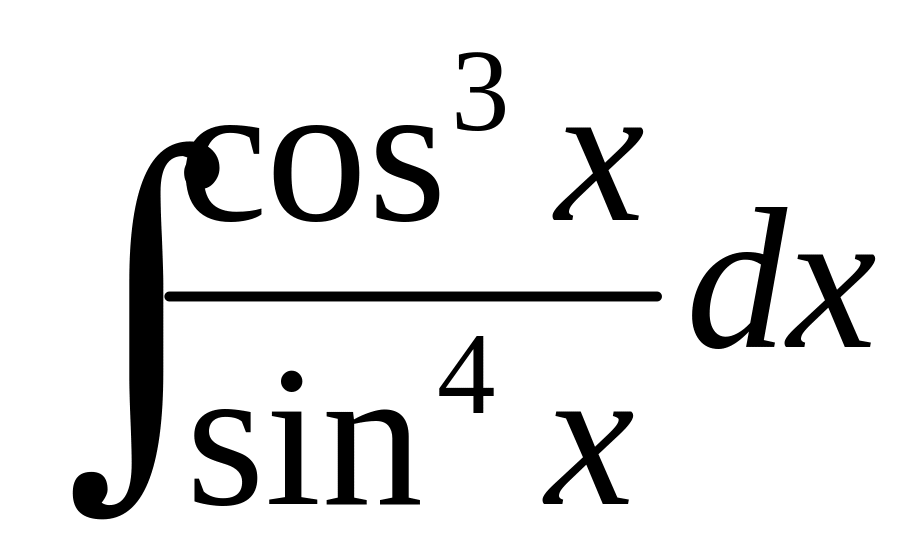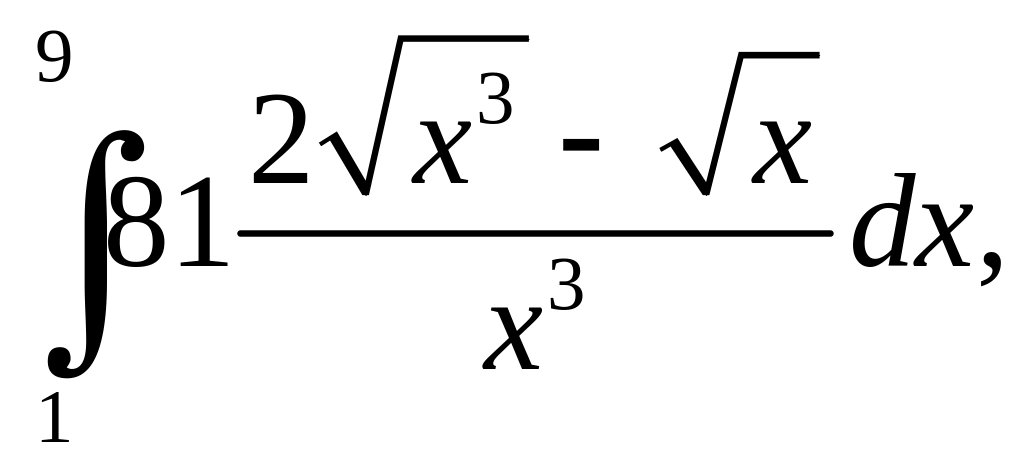
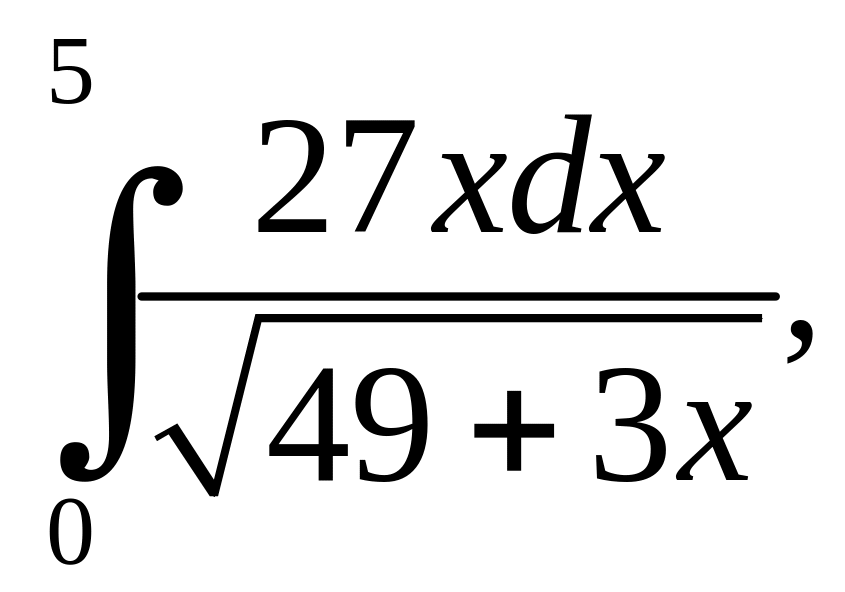