Вариант 4
1. Вычислить неопределенные интегралы:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
.2. Вычислить определенные интегралы:
а)
|
б)
|
в)
|
.3. Зенитная батарея, состоящая из 5 орудий, производит залп по группе, состоящей из 3 самолетов. Каждое из орудий выбирает себе цель наудачу независимо от остальных. Найти вероятность того, что все орудия выстрелят по одному и тому же самолету.
4. Вероятность боя стеклянной тары при погрузке на автомашины равна 0,06, а при транспортировке – 0,05. Какова вероятность боя стеклянной тары?
5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.
а) Найти вероятность того, что при 4 испытаниях событие наступит ровно 2 раза, если вероятность его появления в каждом испытании равна 0,2. б) Вероятность попадания в цель при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена: 1) ровно 85 раз; 2) не менее 70 и не более 80 раз.
6. Дискретная случайная величина Х имеет только два возможных значения: x1 и x2, причем x1 < x2. Вероятность того, что Х примет значение x1 равно 0,4. Найти закон распределения Х, зная математическое ожидание М[X] = 0,4 и дисперсию D[X] = 3,84.
7. Непрерывная случайная величина Х задана функцией распределения
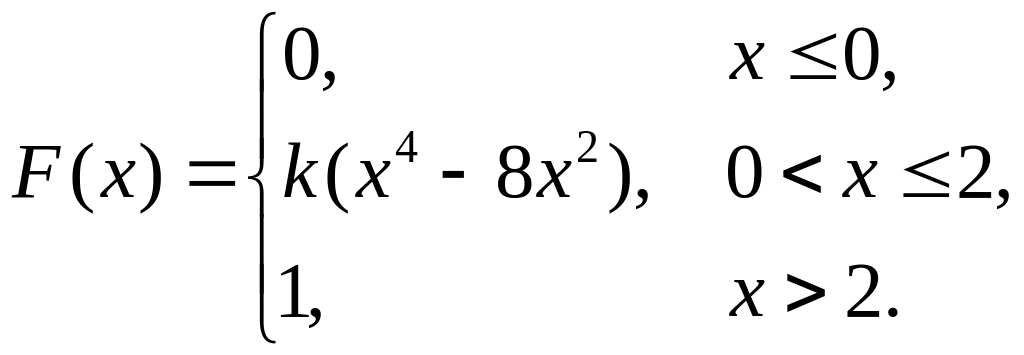
Найти: а) параметр k; б) математическое ожидание; в) дисперсию.
8. Известны математическое ожидание а=5 и среднее квадратичное отклонение =5 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (2, 6); б) отклонения этой величины от математического ожидания не более, чем на .
Вариант 5
1. Вычислить неопределенные интегралы:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
.2. Вычислить определенные интегралы:
а)
|
б)
|
в)
|
.3. 10 вариантов контрольной работы распределяются случайным образом среди 10 студентов, сидящих в один ряд. Найти вероятность того, что варианты с номерами 1 и 2 достанутся рядом сидящим студентам.
4. В электроприборе вышел из строя некоторый элемент. Для его замены решили воспользоваться двумя списанными приборами. Вероятность того, что нужный элемент находится в рабочем состоянии равна 0,4 для каждого прибора. Найти вероятность того, что испорченный элемент будет заменен.
5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.
а) Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 10 выстрелах мишень будет поражена 5 раз. б) Монету бросают 300 раз. Найти вероятность того, что герб появится: 1) ровно 150 раз; 2) от 135 до 145 раз.
6. Дискретная случайная величина Х имеет только два возможных значения: x1 и x2, причем x1 < x2. Вероятность того. что Х примет значение x1 равно 0,3. Найти закон распределения Х, зная математическое ожидание М[X] = 0,8 и дисперсию D[X] = 3,36.
7. Непрерывная случайная величина Х задана функцией распределения
Найти: а) параметр k; б) математическое ожидание; в) дисперсию.
8. Известны математическое ожидание а=4 и среднее квадратичное отклонение =3 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (3, 10); б) отклонения этой величины от математического ожидания не более, чем на =4.