Вариант 22

1. Вычислить неопределенные интегралы:

а)	б)
в)	г)
д)	е) .

2. Вычислить определенные интегралы:

а)

б)

в) .

3. Брошены две игральные кости. Найти вероятности того, что: а) на первой кости выпала 1, б) выпала хотя бы одна 6.

4. Вероятность сдать экзамен студентом равна 0,9. Какова вероятность того, что студент сдаст экзамен со второй попытки?

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) Всхожесть семян составляет 80%. Определить вероятность того, что из 7 посеянных семян взойдет не менее 5.

б) Вероятность попадания стрелком в цель равно 0,95. Найти вероятность того, что при 90 выстрелах он попадет в цель: 1) ровно 85 раз; 2) не менее 83, но не более 88 раз.

6. Дискретная случайная величина Х имеет только два возможных значения: x₁ и x₂, причем x₁ < x₂. Вероятность того, что Х примет значение x₁ равно 0,7. Найти закон распределения Х, зная математическое ожидание М[X] = –1,1 и дисперсию D[X] = 1,89.

7. Непрерывная случайная величина Х задана функцией распределения

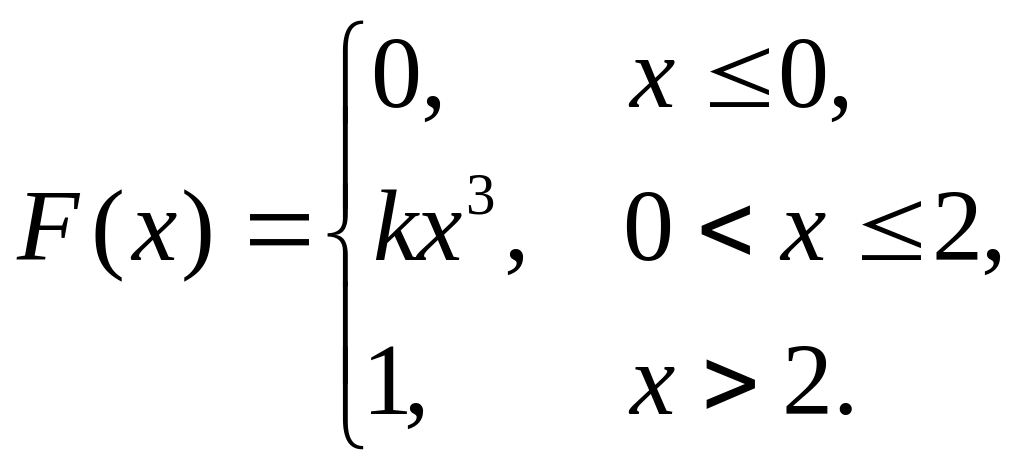
Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а=2 и среднее квадратичное отклонение =4 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (1, 8); б) отклонения этой величины от математического ожидания не более, чем на .

Вариант 23

1. Вычислить неопределенные интегралы:

а)	б)
в)	г)
д)	е) .

2. Вычислить определенные интегралы:

а)

б)

в) .

3. Четырем полевым радиостанциям разрешено во время учений работать на 5 радиоволнах. Выбор волны на каждой станции производится наудачу. Найти вероятность того, что будут использованы различные радиоволны.

4. На начальном участке для мотоциклиста-гонщика имеются 4 препятствия, вероятность остановки на каждом из которых равна 0,1. Вероятность остановки на заключительном участке равна 0,6. Какова вероятность того, что мотоциклист доедет до финиша без единой остановки?

5. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.

а) При передаче сообщения вероятность искажения одного знака равна 0,15. Какова вероятность того. что сообщение из 8 знаков содержит менее 4 искажений?

б) Было посажено 250 деревьев. Вероятность того, что отдельное дерево приживется равно 0,7. Найти вероятность того. что число прижившихся деревьев: 1) равно 190, 2) больше 165, но меньше 185.

6. Дискретная случайная величина Х имеет только два возможных значения: x₁ и x₂, причем x₁ < x₂. Вероятность того, что Х примет значение x₁ равно 0,2. Найти закон распределения Х, зная математическое ожидание М[X] = 2,6 и дисперсию D[X] = 7,84.

7. Непрерывная случайная величина Х задана функцией распределения

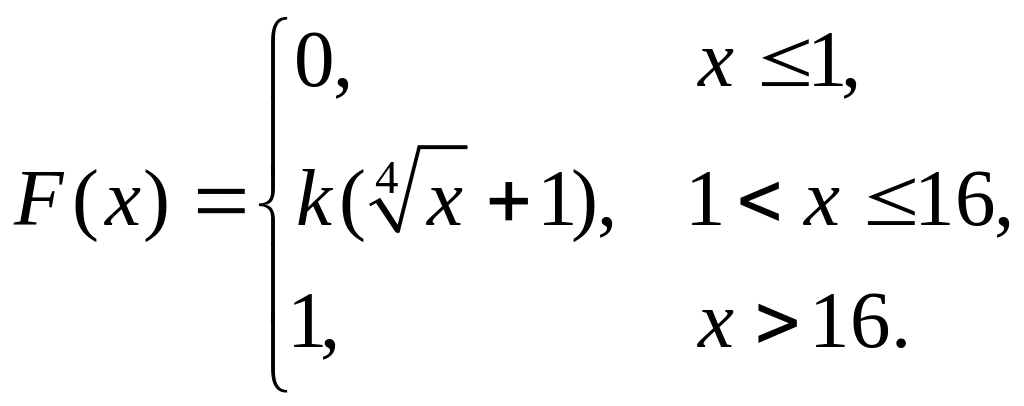
Найти: а) параметр k; б) математическое ожидание; в) дисперсию.

8. Известны математическое ожидание а=2 и среднее квадратичное отклонение =4 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (1, 6); б) отклонения этой величины от математического ожидания не более, чем на .
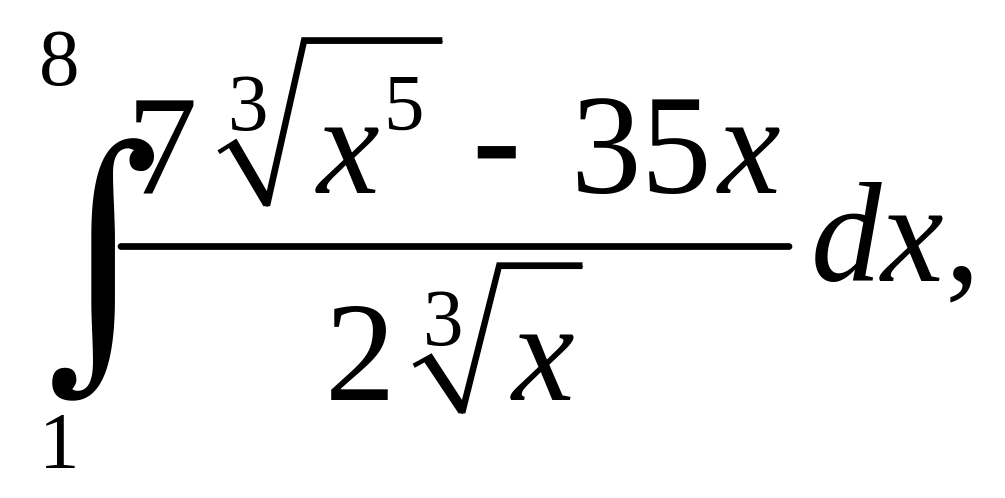
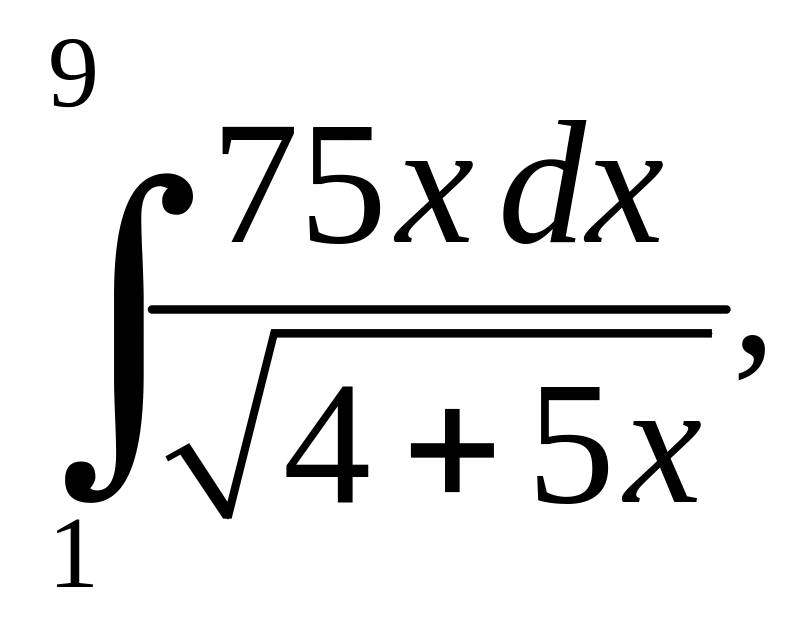
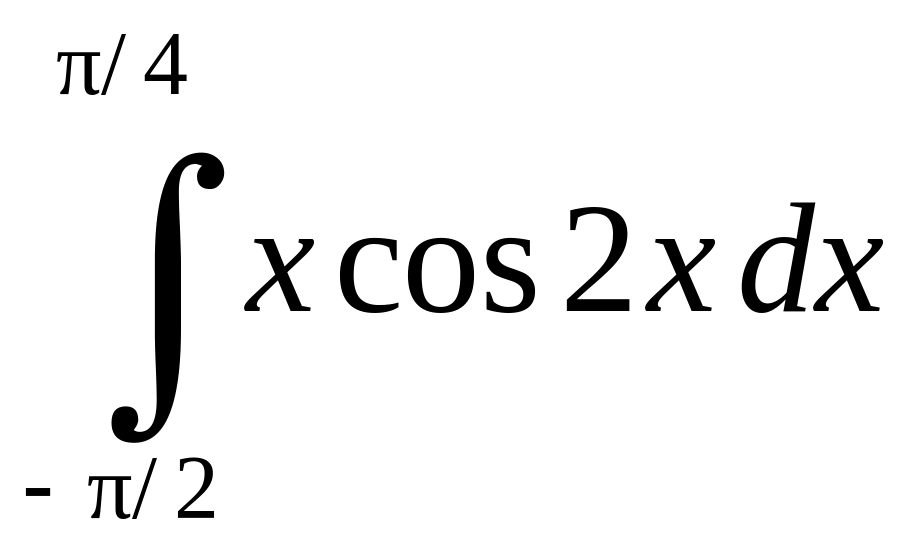