Глава 4. Программная реализация и результаты экспериментальных исследований матричного алгоритма
4.1. Экспериментальные исследования алгоритма
Для проведения исследований, на языке C#, в среде Microsoft Visual Studio 2008, была разработана программа CutGraf. Программа реализует матричный алгоритм, и разработана так, чтобы пользователю было удобно проводить эксперименты по изучению свойств алгоритма в различных условиях. Целью исследования являлось выявление условий применения алгоритма, влияющих на качество решения задачи. Программа CutGraf позволяет получить один из возможных локальных оптимумов. Основные исследования были направлены на поиск возможности перехода от одного локального оптимума к другому и сопоставления их значений.
Экспериментальные
исследования проводились на графах,
содержащих 10, 20 и 30 вершин. Для каждого
графа менялись условия применения
алгоритма: число, размерность и
расположение блоков в шаблоне; стратегия
выбора оценки
- максимальная среди элементов
или первая положительная; коэффициент
заполнения матрицы R ненулевыми элементами
и область изменения их значений. Для
фиксированных условий применения в
ходе эксперимента определялся разброс
значений получаемых локальных оптимумов.
В результате исследования было
установлено, что разброс составляет не
более 10% . С увеличением числа блоков и
различия в их размерностях наблюдалась
тенденция к увеличению разброса. Рост
коэффициента заполнения матрицы
ненулевыми элементами и увеличение их
значений приводил к снижению разброса.
В
ходе исследований была найдена возможность
перехода от одного локального оптимума
к другому. Такой переход осуществляется
следующим образом. Применяя стратегию
преобразования матрицы для положительных
и максимальных оценок
,
получаем некоторый локальный оптимум.
Если работу алгоритма продолжить для
оценок
,
то возможен переход на «склон» к другому
локальному оптимуму. Установлено, что
переход на «склон», как правило, происходит
в тех случаях, когда новое решение имеет
значительное отклонение от достигнутого
ранее. В общем случае, при решении задачи,
сведенья об отклонении отсутствуют,
поэтому предложено дополнить алгоритм
режимом работы с оценками
.
Переход к новому решению выполняется
через оценку
.
Это позволило после получения исходного
локального оптимума частично «прощупать»
его окрестности и улучшить решение или
получить подтверждение того, что оно
далеко не самое плохое.
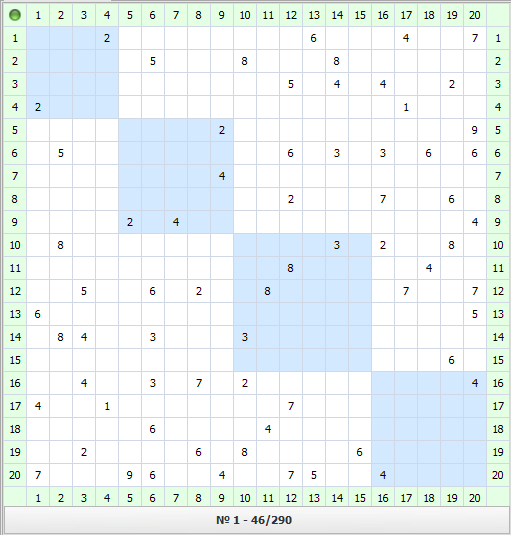
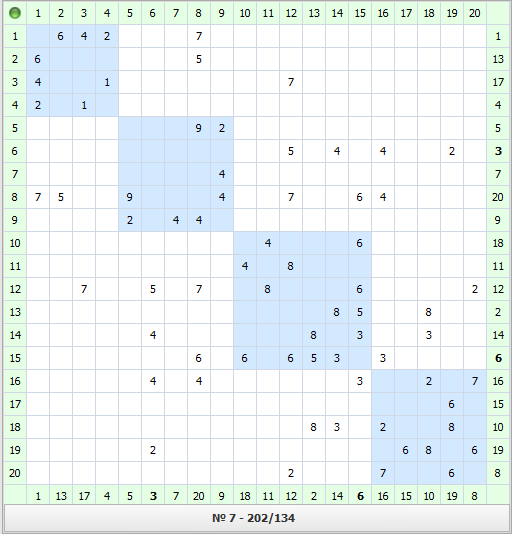
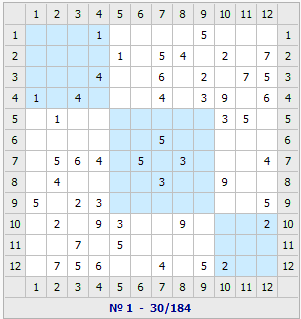
Пример работы алгоритма показан на рис. 7. Под матрицами на рис. 7 в числителе указана сумма весов элементов блоков, а в знаменателе – области сечения Vс. Второй локальный оптимум (рис. 7в) получен путём случайного выбора оценки (рис. 7г) для выхода из локального оптимума, полученного алгоритмом (рис. 7б). При переходе к другому локальному оптимуму следует использовать несколько итераций с отрицательными оценками, а после этого использовать положительные оценки.
а) б)
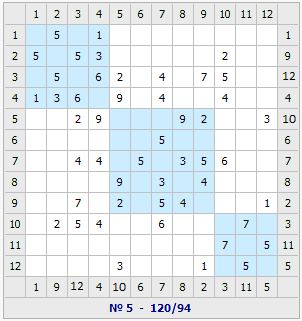
в) г)
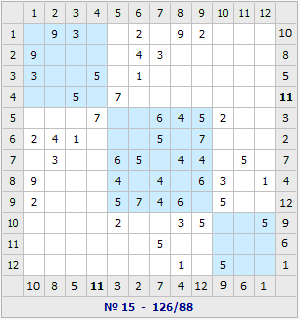
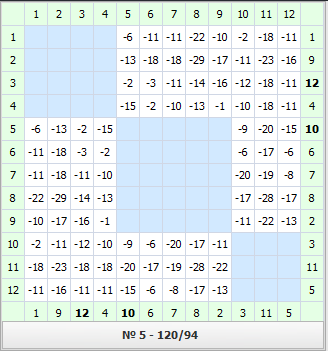
Рис. 7. а – исходный вариант матрицы; б – результат работы алгоритма; в – второй локальный оптимум; г – матрица оценок для первого локального оптимума
|
|
Рис. 8. Разрезание графа, содержащего 20 вершин
|
|
Рис. 9. Разрезание графа, содержащего 30 вершин