Девиз «Работай без ошибок!»

Графовые модели территориально распределённых систем и задачи их декомпозиции

Томск 2010

Реферат

Отчёт по научной работе содержит 38 с., 20 рисунков, 6 источников литературы.

Ключевые слова: территориально распределённая система, топологический граф, двудольный граф, обыкновенный граф, матричный алгоритм разрезания графов, локальный оптимум.

Объектом исследования является графовые модели территориально распределённых систем и методы их декомпозиции.

Цель работы – представление структуры территориальной системы в виде графовой модели и исследование матричного алгоритма решения задачи разрезания обыкновенных графов.

В процессе работы, в среде Microsoft Visual Studio 2008, на языке C#, была разработана программа CutGraf, реализующая матричный алгоритм разрезания графов. С помощью программы проведены экспериментальные исследования данного алгоритма и предложен один из путей его улучшения.

Программа CutGraf может быть использована при определении топологии сети вычислительной системы при проектировании распределённых систем.

Время работы программа не является критичным при решении задач для графов размерностью до 100 вершин (не превышает двух секунд).

Содержание

ВВЕДЕНИЕ 4

Глава 1. Описание предметной области 5

Глава 2. Постановка задачи разрезания графов 11

Глава 3. Матричный алгоритм решения задачи разрезания графов 14

3.1. Основные положения матричного алгоритма 14

3.2. Перемещение элементов матрицы 16

3.3. Выбор элементов для перемещения 18

3.4. Матричный алгоритм и пример его применения 20

Глава 4. Программная реализация и результаты экспериментальных исследований матричного алгоритма 25

4.1. Экспериментальные исследования алгоритма 25

4.2. Описание программы 28

4.3. Руководство для пользователя 29

Заключение 37

Литература 39

Введение

В работе рассматриваются системы, оборудование которых представлено совокупностью объектов и размещено на заданной территории. В территориально распределённых системах расстояние между объектами, как правило, играет важную роль. Наряду с расстояниями могут использоваться другие величины, характеризующие отношения между объектами, например время и (или) стоимость проезда, транспортировки грузов, а при наличии сетевых коммуникаций – их надёжность, пропускная способность, объём передаваемых данных, стоимость эксплуатации.

Глава 1. Описание предметной области

Территории, на которых расположено оборудование распределённых систем, могут быть представлены планами цехов промышленных производств, электронными картами геоинформационных систем [1] с указанием мест расположения пунктов сбора и приёма информации и других объектов. Это могут быть станции гидрометеослужбы, оборудование и газовых месторождений, транспортных и энергетических систем, распределённых систем управления данными и управлениями, систем мониторинга, информационно-телекоммуникационных систем различного назначения. В последующем такие территории будем именовать топологическими полями и представлять их виде координатной плоскости.

На топологическом поле каждый объект представлен точкой (центром объектов) с указанием его координат. Будем считать, что на топологическом поле представлен взвешенный граф. TG=(Q, R) с множеством вершин (объектов) Q={q_i} i=1,2,…,n и множеством рёбер с весами , определяющими расстояния между вершинами q_i и q_j. Данный граф отличается от обыкновенного взвешенного графа [2] тем, что его вершины имеют фиксированные, заданный координатами, места расположения на плоскости, а каждая пара вершин q_i и q_j связана ребром с весом , который равен расстоянию между соответствующими точками плоскости.

Граф TG будем именовать топологическим. На топологическом поле граф TG визуально представляется множеством вершин (точек) с заданием координат (x_i, y_i). Граф TG может быть представлен также матрицей расстояний , которая получается на основе визуального представления графа. Матрица R является симметричной, а диагональные элементы .

При проектировании территориально распределённых систем управления, как правило, возникает задача разбиения множества объектов на заданное число подмножеств так, чтобы сумма расстояний между объектами в подмножествах была минимальной.

Данная задача соответствует получению компактного разбиения [3] и может рассматриваться, как задача разрезания графа на подграфы. В последующем мы будем рассматривать обыкновенные графы, вершины которых не зависят от координат на топологическом поле. Такие графы возникают при проектировании распределённых систем управления, построенных на базе совокупности контроллеров (станций), связанных в локальную сеть. Для таких систем на топологическом поле указываются места расположения датчиков информации и исполнительных механизмов систем управления, пунктов сбора и обработки первичных данных и пунктов, в которые поступают данные.

Точки с координатами этих мест будем именовать терминальными точками или просто точками, если это не приводит к неоднозначному толкованию. В каждой терминальной точке данные либо зарождаются либо используются. Все терминальные точки подключаются к станциям так, чтобы минимизировать суммарную длину линий связи. После этого решаются задачи, связанные с определением архитектуры и топологии сети вычислительной системы, реализующей функции управления в проектируемой системе.

Для решения данной задачи разрабатывается модель алгоритмов, реализующих программное обеспечение в форме графа потока данных (ГПД)[4]. Пример ГПД с указанием объёмов данных, передаваемых между модулями графа, показан на рис.1.

ГПД содержит программные модули (на рис.1 показаны в виде планок) и данные (показаны в виде кружков). Рёбра ГПД показывают отношение данных и модулей. Веса рёбер характеризуют объём данных, передаваемых между модулями, полученные с учётом реальных частот срабатывания модулей при функционировании системы. Пунктирными линиями на рис.1 показано распределение модулей и данных по станциями вычислительной системы. На основе этого распределения можно построить граф передачи данных между станциями, показанный на рис. 2 [5].

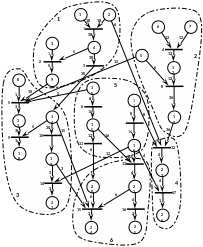
Рис. 1. Граф передачи данных между модулями ГПД

Вершины графа соответствуют станциям, а веса рёбер соответствуют объёму данных, передаваемых между станциями. На основе данного графа можно построить такую архитектуру вычислительной системы, в которой минимизируется суммарное время на передачу данных в сети.

С этой целью рассматриваются возможные варианты организации сети и среди них выбирается вариант, который в наибольшей мере соответствует графу передачи данных. Варианты базовых сетей представлены на рис. 3. Каждая базовая сеть строится на основе нескольких магистралей, показанных на рис. 3 жирными линиями. К каждой магистрали может подключаться некоторое число станций, причём данные могут передаваться как между станциями, подключенными к одной магистрали, так и между станциями, подключенными к разным магистралям. Передача данных внутри одной магистрали предпочтительнее, т.к. при использовании нескольких магистралей время передачи увеличивается.

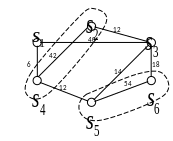
Рис. 2. Граф передачи данных

Каждый пример базовой сети сопровождается диаграммой, которая иллюстрирует возможную загрузку магистралей сети при передаче данных между станциями. При этом предполагается, что станции подключены к каждой магистрали сети, а передача данных осуществляется как между станциями одной магистрали, так и между станциями разных магистралей. Длины отрезков, отражающих объемы передаваемых данных, приняты произвольно. Над каждым отрезком указан перечень магистралей, участвующих в передаче данных. Например, запись 1-4-2 над отрезками диаграммы (рис. 3-г) обозначает загрузку магистралей М1, М4, М2 при передаче данных между станциями, подключенными к магистралям М1 и М2. Заметим также, что параллельно с этой передачей могут передаваться данные между станциями, подключенными к магистрали М3, то есть отрезок 3 на диаграмме рис. 3-г может размещаться параллельно отрезкам 1-4-2.

Анализ приведенных на рис. 3 базовых сетей по соответствующим диаграммам позволяет сделать ряд выводов.

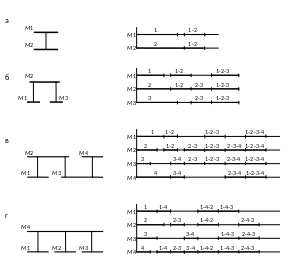
Рис. 3. Примеры базовых сетей и диаграмм загрузки магистралей

В сети (а) станции желательно подключать к магистралям М1 и М2 так, чтобы отрезки 1 и 2 были примерно равны, а отрезок 1-2 был минимальной длины. Для сети (б) критичной по загрузке является магистраль М2. В сети (в) такими магистралями являются М2 и М3, а в сети (г) магистраль М4. Для данных сетей наилучшим вариантом подключения станций к магистралям будет такой вариант, который обеспечивает равную и минимальную загрузку магистралей. Например, для сети (б) условие равенства загрузки магистралей можно записать в виде:[1]+[1-2]=[2]+[1-2]+[2-3]=[3]+[2-3]. Здесь квадратные скобки обозначают длину соответствующих отрезков. Аналогичные условия равенства загрузки магистралей можно записать для сетей (в) и (г).

Минимально возможная загрузка магистралей достигается в случае, если подключение станций к магистралям удается выполнить таким образом, что между станциями, подключенными к разным магистралям, данные не передаются или их объём минимален. Это достигается решением задачи разрезания графа передачи данных на минимально связанные подграфы. В каждый подграф попадут станции, которые будут подключены к одной магистрали и, следовательно, объём передаваемых данных между станциями разных магистралей будет минимален.