По связям с окружением:

• открытые (с определенным окружением, то есть, по крайней мере, с одним выходом или выходом);

• замкнутые (без связей с окружением).

  3. По изменению состояния:

     • динамические (состояние меняется во времени);

     • статические (состояние не меняется во времени).

4. По характеру функционирования:

   • детерминированные (в зависимости от состояния системы можно однозначно судить об ее функционировании);

   • стохастические (можно только с определенной вероятность предполагать возможные варианты функционирования).

     5. По типу элементов (в смысле их конкретности):

        • конкретные (элементы – реальные объекты);

        • абстрактные (элементы – абстрактные объекты).

6. По характеру зависимости выходов:

   • комбинаторные (выход зависит только от входа);

   • секвентивные (выход зависит от входа и от других величин).

7. По степени сложности структуры:

• предельно сложные (например, мозг человека, национальная экономика);

• очень сложные (например, автоматизированное предприятие, производственный комплекс);

• сложные (например, автомобиль);

• простые (например, болтовое соединение).

  6. По виду элементов:

     • системы типа «объект» (элементами являются предметы, например, двигатель, автомобиль);

     • системы типа «процесс» (элементами являются операции, например, изготовление или ремонт автомобиля).

2.Введение в теорию вероятностей и математическую статистику

2.1.Случайная величина

Случайная величина как фундаментальное понятие теории вероятности имеет большое значение в ее приложениях. Это понятие является абстрактным выражением случайного события. Более того, оперировать со случайными величинами иногда более удобно, чем со случайными событиями.

Случайной называется величина, которая в результате опыта может принять то или иное (но только одно) значение (до опыта неизвестно, какое именно).

События принято обозначать большими буквами латинского алфавита, вероятность буквой Р, например, Р(А). Реализации события (случайные величины) обозначаются малыми буквами: a₁, a₂, …, a_n.

Поскольку в теории вероятностей и математической статистике рассматриваются массовые явления, то случайная величина, как правило, характеризуется возможными значениями и их вероятностями.

Среди встречающихся в практике случайных величин можно выделить дискретные и непрерывные.

Дискретными случайными величинами называются такие, которые принимают только отделенные друг от друга значения и могут быть заранее перечислены. Например, количество автомобилей на заданном километровом участке дороги в конкретный момент времени; число бракованных узлов деталей автомобиля в партии из n штук.

Для дискретных случайных величин характерно, что они принимают отдельные, изолированные значения, которые можно заранее перечислить. Например, количество автомобилей на заданном участке дороги может принимать только целочисленные значения 0, 1,2, ..., п и зависит от времени суток и интенсивности движения.

Существуют случайные величины другого типа, которые чаще встречаются и имеют большое практическое значение.

Непрерывной случайной величиной называется такая, возможные значения которой непрерывно заполняют некоторый промежуток (интервал числовой оси). Интервал числовой оси может быть конечным или бесконечным. Примерами непрерывных случайных величин являются время безотказной работы автомобиля в заданных дорожных условиях, скорость движения автомобиля на заданной дороге, ошибка измерения.

В отличие от дискретных возможные значения непрерывных случайных величин нельзя заранее перечислить, так как они непрерывно заполняют некоторый промежуток.

Случайные величины обозначаются обычно большими буквами латинского алфавита - X, Y, Z, Т, а их возможные значения соответствующими малыми x_i, y_i, z_i, t_i, где i = 1, 2, .... п.

Рассмотрим дискретную случайную величину X с возможными значениями x₁, x₂, …, x_n. В результате проведения многократных опытов величина Т может принять каждое из значений x_i, т. е.:

X = x₁; X = x₂; …; X = x_n.

Обозначим вероятности этих событий буквой р с соответствующими индексами:

P(X = x₁)= p₁; P(X = x₂)= p₂; …; P(X = x_n)= p_n.

Последнюю формулу следует читать так: вероятность того, что случайная величина Т примет конкретное значение x₁, равна p₁ и т.д.

Исходя из того, что события x_i образуют полную группу несовместимых событий, т. е. никаких других событий произойти не может, сумма вероятностей всех возможных значений случайной величины Т равна единице.

Эта суммарная вероятность каким-то образом распределена между отдельными значениями случайной величины

Дискретную случайную величину можно полностью описать с вероятностной точки зрения, если точно указать вероятность каждого события, т. е. задать это распределение. Этим будет установлен закон распределения случайной величины.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Зная его, можно до опыта судить о том, какие значения случайной величины будут появляться чаще и какие реже. Способы или формы представления закона распределения случайной величины различны.

Простейшей формой задания закона распределения дискретной случайной величины Т является ряд распределения или таблица, в которой перечислены возможные значения этой величины и соответствующие им вероятности:

Чтобы придать ряду распределения дискретных случайных величин более наглядный вид, его часто изображают графически.

При графическом представлении все возможные значения случайной величины откладывают по оси абсцисс, а соответствующие вероятности - по оси ординат.

Вершины полученных ординат обычно соединяют прямыми или пунктирными линиями. Это особенно целесообразно, если на одном графике представлено несколько кривых распределений. Соединяют вершины только для наглядности, так как в промежутках между соседними значениями случайная величина X значений принять не может, так как она дискретная, а ее вероятность в этих промежутках равна нулю. Такая фигура, изображенная на рис. 2.1, называется многоугольником распределения.

Многоугольники распределения могут принимать различные формы. Однако все они обладают общим свойством: сумма ординат многоугольника распределения, представляющая сумму вероятностей всех возможных значений случайной величины, всегда равна единице. Следует особо разграничить деление случайных величин на дискретные и непрерывные. Так, ряд распределения является удобной формой представления закона распределения для дискретной случайной величины, характеризуемой конечным числом возможных значений. Однако для непрерывной случайной величины ряд распределения вообще нельзя построить, поскольку она характеризуется бесчисленным множеством возможных значений, которые сплошь заполняют некоторый промежуток, и перечислить их в таблице трудно.

Различные диапазоны возможных значений случайной величины все же являются неодинаково вероятными, и для непрерывной величины существует распределение величин интервалов, а не конкретных значений.

Для количественной оценки этого распределения вероятностей используется не вероятность события X = x, а вероятность события X < x (x - некоторая текущая величина).

Вероятность этого события зависит от x является функцией от x, которая называется функцией распределения случайной величины Т и обозначается F(x).

Функцию распределения F(x) иногда называют интегральной функцией, или интегральным законом, распределения. Она существует для дискретных и непрерывных случайных величин и является самой универсальной их характеристикой

График функции F(x) представляет неубывающую функцию, значения которой начинаются от 0 и доходят до 1, причем в отдельных точках функция может иметь скачки (разрыв).

Обычно для дискретной случайной величины функция распределения F(x) всегда разрывная ступенчатая, скачки которой происходят в точках, соответствующих возможным значениям и равны вероятностям этих значений. Для непрерывной случайной величины она непрерывна во всех точках.

Графическое представление функции распределения удобно для решения практических задач, связанных с определением вероятности того, что случайная величина примет значение, заключенное в некоторых пределах от x₁ до x₂. Это событие равносильно попаданию величины X на участок от x₁ до x₂ и равно приращению функции распределения на этом участке

Р(x₁  X  x₁) = F(x₁) – F(x₂).

2.2.Плотность распределения

Функция распределения дискретной и непрерывной случайных величин является ее вероятностной характеристикой. Однако для непрерывной случайной величины более наглядное представление о характере ее распределения в окрестности различных точек дает функция, называемая плотностью распределения вероятности, или дифференциальным законом распределения случайной величины.

Плотностью распределения случайной величины в точке x является предел отношения вероятности попадания непрерывной случайной величины на элементарный участок от x до x + x к длине его, когда x стремится к нулю

.

Считая функцию распределения F(x) дифференцируемой и перейдя к пределу, получим

.

т. е. плотность f(x) равна производной от функции распределения F(x).

Плотность распределения f(x) указывает на то, как часто появляется случайная величина X в некоторой окрестности точки x при многократном повторении опытов.

Кривая, изображающая плотность распределения f(x) случайной величины, называется кривой распределения (рис. 2.2).

Как и функция распределения, плотность распределения - одна из форм закона распределения. В противоположность функции распределения плотность не универсальна, так как она существует только для непрерывных случайных величин.

Основные свойства плотности распределения случайной величины следующие:

• плотность распределения – неотрицательная функция, т. е. кривая распределения лежит не ниже оси абсцисс;

• интеграл в бесконечных пределах от плотности распре­деления равен единице, т. е. площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

2.3.Числовые характеристики случайных величин

При решении многих практических задач не всегда нужно характеризовать случайную величину полностью, т. е. определять законы распределения. Кроме того, построение функции или ряда распределений для дискретной, а плотности - для непрерывной случайной величины громоздко и излишне.

Иногда достаточно указать отдельные числовые параметры, частично характеризующие особенности распределения. Необходимо знать некоторое среднее значение каждой случайной величины, около которого группируется ее возможное значение, или степень разбросанности этих значений относительно среднего и т. п.

Характеристики наиболее существенных особенностей распределения называются числовыми характеристиками случайной величины. С их помощью облегчается решение многих вероятностных задач без определения для них законов распределения.

Важнейшей характеристикой положения случайной величины на числовой оси является математическое ожидание М[X] = а, которое иногда называется средним значением случайной величины. Для дискретной случайной величины X с возможными значениями x₁, x₂, …, x_n и вероятностями p₁, p₂,…, p_n его определяют по формуле

.

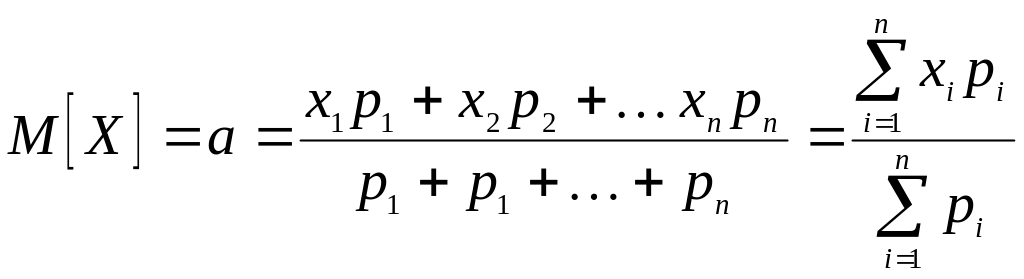Учитывая, что =1, можно записать

.

Таким образом, математическим ожиданием дискретной случайной величины называется сумма произведений возможных ее значений на их вероятности. Среднее арифметическое значение наблюдаемых значений случайной величины при большом числе опытов приближается к ее матема­тическому ожиданию.

Для непрерывной случайной величины X математической ожидание определяется не суммой, а интегралом

,

где f(x) — плотность распределения величины X.

Математическое ожидание существует не для всех случайных величин. Для некоторых из них сумма, или интеграл, расходится, и, следовательно, математического ожидания не существует. В этих случаях по соображениям точности следует ограничивать область возможных изменений случайной величины X, для которых сумма, или интеграл, будут сходиться.

На практике применяются и такие характеристики положения случайной величины, как мода и медиана.

Модой случайной величины называется ее наиболее вероятное значение. В общем случае мода и математическое ожидание не совпадают.

Медианой случайной величины X называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины, т. е. это абсцисса точки, в которой ограниченная кривой распределения площадь делится пополам. Для симметричного распределения все три характеристики совпадают.

Кроме математического ожидания, моды и медианы в теории вероятностей используются и другие характеристики, каждая из которых описывает определенное свойство распределения. Например, числовыми характеристиками, характеризующими рассеивание случайной величины, т. е. показывающими, насколько тесно сгруппированы ее возможные значения около математического ожидания, являются дисперсия и среднее квадратическое отклонение. Они существенно дополняют случайную величину, так как в практике часто встречаются случайные величины с равными математическими ожиданиями, но различными распределениями. При определении характеристик рассеивания используют разность между случайной величиной X и ее математическим ожиданием, т. е.

,

где а = М[X] — математическое ожидание.

Эта разность называется центрированной случайной величиной, соответствующей величине X, и обозначается :

.

Дисперсия случайной величины - это математическое ожидание квадрата отклонения величины от ее математического ожидания, т. е.:

D[X]=M[(X – a)²], или

D[X]=M[ ²].

Дисперсия случайной величины является удобной характеристикой рассеивания и разбросанности значений случайной величины около ее математического ожидания. Однако она лишена наглядности, так как имеет размерность квадрата случайной величины.

Для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Такой величиной является среднее квадратическое отклонение случайной величины, которое представляет собой положительный квадратный корень из ее дисперсии.

Математическое ожидание, мода, медиана, дисперсия, среднее квадратическое отклонение - наиболее часто используемые числовые характеристики случайных величин. При решении практических задач, когда невозможно определить закон распределения, приблизительным описанием случайной величины являются ее числовые характеристики, выражающие какое-либо свойство распределения.

Кроме основных характеристик распределения центра (математического ожидания) и рассеивания (дисперсии) часто нужно описать другие важные характеристики распределения - симметрию и островершинность, которые можно представить с помощью моментов распределения.

Распределение случайной величины, полностью задано, если известны все его моменты. Однако многие распределения можно полностью описать с помощью первых четырех моментов, которые являются не только параметрами, описывающими распределения, но имеют также важное значение при подборе эмпирических распределений, т. е. вычислив числовые значения моментов для заданного статистического ряда и, использовав специальные графики, можно определить закон распределения.

В теории вероятностей различают моменты двух видов: начальные и центральные.

Начальным моментом k-го порядка случайной величины Т называют математическое ожидание величины X^k, т. е.

.

Следовательно, для дискретной случайной величины он выражается суммой

,

а для непрерывной – интегралом

.

Среди начальных моментов случайной величины особое значение имеет момент первого порядка, который является математическим ожиданием. Начальные моменты высших порядков используются, главным образом, для вычисления центральных моментов.

Центральным моментом k-го порядка случайной величины называют математическое ожидание величины (X - М [X])^k

,

где а = М [X].

Для дискретной случайной величины он выражается суммой

,

а для непрерывной – интегралом

.

Среди центральных моментов случайной величины особое значение имеет центральный момент второго порядка, который представляет дисперсию случайной величины.

Центральный момент первого порядка всегда равен нулю.

Третий начальный момент характеризует асимметрию (скошенность) распределения и по результатам наблюдений для дискретной и непрерывной случайных величин определяется соответствующими выражениями:

; .

Поскольку он имеет размерность куба случайной величины, то, чтобы получить безразмерную характеристику, ₃ делят на среднее квадратическое отклонение в третьей степени

.

Полученная величина называется коэффициентом асимметрии и в зависимости от знака характеризует положительную (As > 0) или отрицательную (As < 0) скошенность распределения (рис. 2.3).

Четвертый центральный момент ₄ характеризует островершинность или плосковершинность распределения и для дискретных и непрерывных случайных величин определяется соответствующими выражениями:

; .

Однако на практике эти свойства распределения описываются с помощью безразмерной характеристики, называемой эксцессом

.

Кривая нормального распределения с эксцессом, равным нулю, является как бы эталоном, с которым сравнивают другие распределения.

Более островершинные кривые имеют положительный эксцесс, а более плосковершинные - отрицательный.

Таблица

Функции распределения наиболее распространенных законов

3. Марковский случайный процесс

3.1.Основные понятия марковских процессов

Для математического описания многих операций, развивающихся в форме случайного процесса, может быть с успехом применен математический аппарат, разработанный в теории вероятностей для Марковских случайных процессов.

Функция X(t) называется случайной, если ее значение при любом аргументе t является случайной величиной.

Случайная функция X(t), аргументом которой является время, называется случайным процессом.

Марковские процессы являются частным видом случайных процессов. Особое место марковских процессов среди других классов случайных процессов обусловлено следующими обстоятельствами: для марковских процессов хорошо разработан математический аппарат, позволяющий решать многие практические задачи; с помощью марковских процессов можно описать (точно или приближенно) поведение достаточно сложных систем.

Определение. Случайный процесс, протекающий в какой-либо системе S, называется марковским (или процессом без последействия), если он обладает следующим свойством: для любою момента времени t₀ вероятность любого состояния системы в будущем (при t > t₀) зависит только от ее состояния в настоящем (при t = t₀) и не зависит от того, когда и каким образом система S пришла в это состояние. То есть в марковском случайном процессе будущее развитие процесса не зависит от его предыстории.

Классификация марковских процессов. Классификация марковских случайных процессов производится в зависимости от непрерывности или дискретности множества значений функции X(t) и параметра t. Различают следующие основные виды марковских случайных процессов:

• с дискретными состояниями и дискретным временем (цепь Маркова);

• с непрерывными состояниями и дискретным временем (марковские последовательности);

• с дискретными состояниями и непрерывным временем (непрерывная цепь Маркова);

• с непрерывным состоянием и непрерывным временем.

Здесь будут рассматриваться только марковские процессы с дискретными состояниями S₁, S₂,…, S_n. То есть эти состояния можно перенумеровать одно за другим, а сам процесс состоит в том, что система случайным образом скачком меняет свое состояние.

Граф состояний. Марковские процессы с дискретными состояниями удобно иллюстрировать с помощью так называемого графа состояний (рис. 1.1.), где квадратиками обозначены состояния S₁, S₂, ... системы S, а стрелками - возможные переходы из состояния в состояние. На графе отмечаются только непосредственные переходы, а не переходы через другие состояния. Возможные задержки в прежнем состоянии изображают «петлей», т. е. стрелкой, направленной из данного состояния в него же. Число состояний системы может быть как конечным, так и бесконечным (но счетным).

Рис. 3.3. Граф состояний системы S

Задача 1. Система S – автомобиль, которая может находиться в одном из пяти состояний.

S₁ – исправна, работает;

S₂ – неисправна, ожидает осмотра;

S₃ –осматривается;

S₄ – ремонтируется;

S₅ – списана.

Построить граф состояний системы.

Задача 2. Техническое устройство S состоит из 2-х узлов: 1 и 2, каждый из которых может в любой момент времени отказать. У каждого узла может быть только 2 состояния. 1 – исправен, 2 – неисправен. Построить граф состояний системы.

Задача 3. Построить граф состояний в условиях предыдущей задачи, предполагая, что ремонт узлов в ходе процесса не производится.

Задача 4. Техническое устройство S состоит из 2-х узлов: 1 и 2, каждый из которых может в любой момент времени отказать. Каждый узел, перед тем как начать восстанавливаться подвергается осмотру с целью локализации неисправности. Состояния системы нумеруются 2-мя индексами: S_ij (i – состояния первого узла, j – состояния второго узла). У каждого узла три состояния (работает, осматривается, восстанавливается).

3.2.Марковские цепи

Марковский случайный процесс с дискретными состояниями и дискретным временем называют марковской цепью. Для такого процесса моменты t₁, t₂, …, когда система S может менять свое состояние, рассматривают как последовательные шаги процесса, а в качестве аргумента, от которого зависит процесс, выступает не время t, а номер шага 1, 2, ..., k, ... Случайный процесс в этом случае характеризуется последовательностью состояний S(0), S(1), S(2), ..., S(k), ..., где S(0) - начальное состояние системы (перед первым шагом); S(1) - состояние системы после первого шага; S(k) - состояние системы после k-го шага...

Событие {S(k) = S_i}, состоящее в том, что сразу после k-го шага система находится в состоянии S_i (i = 1, 2, ...), является случайным событием. Последовательность состояний S(0), S(1), ..., S(k), ... можно рассматривать как последовательность случайных событий. Такая случайная последовательность событий называется марковской цепью, если для каждого шага вероятность перехода из любого состояния S_i в любое S_j не зависит от того, когда и как система пришла в состояние S_i. Начальное состояние S(0) может быть заданным заранее или случайным.

Вероятностями состояний цепи Маркова называются вероятности P_i(k) того, что после k-го шага (и до (k + 1)-го) система S будет находиться в состоянии S_i (i = 1, 2, ..., n). Очевидно, для любою k.

Начальным распределением вероятностей Марковской цепи называется распределение вероятностей состояний в начале процесса:

P₁(0), P₂(0), …, P_i(0), …, P_n(0).

В частном случае, если начальное состояние системы S в точности известно S(0) = S_i, то начальная вероятность Р_i(0) = 1, а все остальные равны нулю.

Вероятностью перехода (переходной вероятностью) на k-м шаге из состояния S_i в состояние S_j называется условная вероятность того, что система S после k-го шага окажется в состоянии S_j при условии, что непосредственно перед этим (после k - 1 шага) она находилась в состоянии S_i.

Поскольку система может пребывать в одном из n состояний, то для каждого момента времени t необходимо задать n² вероятностей перехода P_ij, которые удобно представить в виде следующей матрицы:

где Р_ij – вероятность перехода за один шаг из состояния S_i в состояние S_j;

Р_ii – вероятность задержки системы в состоянии S_i.

Такая матрица называется переходной или матрицей переходных вероятностей.

Если переходные вероятности не зависят от номера шага (от времени), а зависят только от того, из какого состояния в какое осуществляется переход, то соответствующая цепь маркова называется однородной.

Переходные вероятности однородной Марковской цепи Р_ij образуют квадратную матрицу размера n m. Отметим некоторые ее особенности.

1. Каждая строка характеризует выбранное состояние системы, а ее элементы представляют собой вероятности всех возможных переходов за один шаг из выбранного (из i-го) состояния, в том числе и переход в самое себя.

2. Элементы столбцов показывают вероятности всех возможных переходов системы за один шаг в заданное (j-е) состояние (иначе говоря, строка характеризует вероятность перехода системы из состояния, столбец - в состояние).

3. Сумма вероятностей каждой строки равна единице, так как переходы образуют полную группу несовместных событий:

4. По главной диагонали матрицы переходных вероятностей стоят вероятности Р_ii того, что система не выйдет из состояния S_i, а останется в нем.

Если для однородной Марковской цепи заданы начальное распределение вероятностей и матрица переходных вероятностей , то вероятности состояний системы P_i(k) (i, j = 1, 2, …, n) определяются по рекуррентной формуле:

, (3.0)

Пример 1. Рассмотрим процесс функционирования системы - автомобиль. Пусть автомобиль (система) в течение одной смены (суток) может находиться в одном из двух состояний: исправном (S₁) и неисправном (S₂). Граф состояний системы представлен на рис. 3.2.

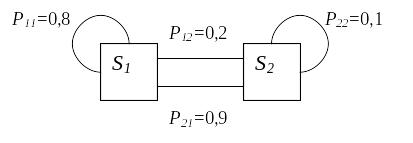
Рис. 3.4.Граф состояний автомобиля

В результате проведения массовых наблюдений за работой автомобиля составлена следующая матрица вероятностей перехода:

где P₁₁ = 0,8 – вероятность того, что автомобиль останется в исправном состоянии;

P₁₂ = 0,2 – вероятность перехода автомобиля из состояния «исправен» в состояние «неисправен»;

P₂₁ = 0,9 – вероятность перехода автомобиля из состояния «неисправен» в состояние «исправен»;

P₂₂ = 0,1 – вероятность того, что автомобиль останется в состоянии «неисправен».

Вектор начальных вероятностей состояний автомобиля задан , т.е. Р₁(0) = 0 и Р₂(0)=1.

Требуется определить вероятности состояний автомобиля через трое суток.

Используя матрицу переходных вероятностей и формулу (3.1), определим вероятности состояний P_i(k) после первого шага (после первых суток):

P₁(1) = P₁(0)P₁₁ + P₂(0)P₂₁ = 0·0,8 + 1·0,9 = 0,9;

P₂(1) = P₁(0)P₁₂ + P₂(0)P₂₂ = 0·0,2 + 1·0,1 = 0,2.

Вероятности состояний после второго шага (после вторых суток) таковы:

P₁(2) = P₁(1)P₁₁ + P₂(1)P₂₁ = 0,90,8 + 0,10,9 = 0,81;

P₂(2) = P₁(1)P₁₂ + P₂(1)P₂₂ = 0,90,2 + 0,10,1 = 0,19.

Вероятности состояний после третьего шага (после третьих суток) равны

P₁(3) = P₁(2)P₁₁ + P₂(2)P₂₁ = 0,810,8 + 0,190,9 = 0,819;

P₂(3) = P₁(2)P₁₂ + P₂(2)P₂₂ = 0,810,2 + 0,190,1 = 0,181.

Таким образом, после третьих суток автомобиль будет находиться в исправном состоянии с вероятностью 0,819 и в состоянии «неисправен» с вероятностью 0,181.

Пример 2. В процессе эксплуатации ЭВМ может рассматриваться как физическая система S, которая в результате проверки может оказаться в одном из следующих состояний: S₁ - ЭВМ полностью исправна; S₂ - ЭВМ имеет неисправности в оперативной памяти, при которых она может решать задачи; S₃ - ЭВМ имеет существенные неисправности и может решать ограниченный класс задач; S₄ - ЭВМ полностью вышла из строя.

В начальный момент времени ЭВМ полностью исправна (состояние S₁). Проверка ЭВМ производится в фиксированные моменты времени t₁, t₂, t₃. Процесс, протекающий в системе S, может рассматриваться как однородная марковская цепь с тремя шагами (первая, вторая, третья проверки ЭВМ). Матрица переходных вероятностей имеет вид

Определить вероятности состояний ЭВМ после трех проверок.

Решение. Граф состояний имеет вид, показанный на рис. 3.3. Против каждой стрелки проставлена соответствующая вероятность перехода. Начальные вероятности состояний P₁(0) = 1, P₂(0) = P₃(0) = P₄(0) = 0.

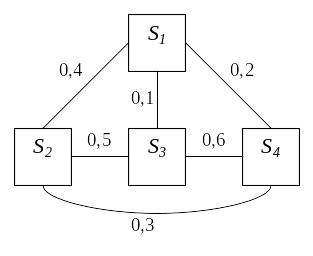
Рис. 3.5. Граф состояний ЭВМ

По формуле (3.1), учитывая в сумме вероятностей только те состояния, из которых возможен непосредственный переход в данное состояние, находим:

P₁(1) = P₁(0)P₁₁ = 10,3 = 0,3;

P₂(1) = P₁(0)P₁₂ = 10,4 = 0,4;

P₃(1) = P₁(0)P₁₃ = 10,1 = 0,1;

P₄(1) = P₁(0)P₁₄ = 10,2 = 0,2;

P₁(2) = P₁(1)P₁₁ = 0,30,3 = 0,09;

P₂(2) = P₁(1)P₁₂ + P₂(1)P₂₂ = 0,30,4 + 0,40,2 = 0,20;

P₃(2) = P₁(1)P₁₃ + P₂(1)P₂₃ + P₃(1)P₃₃ = 0,27;

P₄(2) = P₁(1)P₁₄ + P₂(1)P₂₄ + P₃(1)P₃₄ + P₄(1)P₄₄ = 0,44;

P₁(3) = P₁(2)P₁₁ = 0,090,3 = 0,027;

P₂(3) = P₁(2)P₁₂ + P₂(2)P₂₂ = 0,090,4 + 0,200,2 = 0,076;

P₃(3) = P₁(2)P₁₃ + P₂(2)P₂₃ + P₃(2)P₃₃ = 0,217;

P₄(3) = P₁(2)P₁₄ + P₂(2)P₂₄ + P₃(2)P₃₄ + P₄(2)P₄₄ = 0,680.

Итак, вероятности состояний ЭВМ после трех проверок следующие: P₁(3) = 0,027; P₂(3) = 0,076; P₃(3) = 0,217; P₄(3) = 0,680.

Задача 1. По некоторой цели ведется стрельба четырьмя выстрелами в моменты времени t₁, t₂, t₃, t₄.

Возможные состояния системы: S₁ – цель невредима; S₂ – цель незначительно повреждена; S₃ – цель получила значительные повреждения; S₄ – цель полностью поражена. В начальный момент времени цель находится в состоянии S₁. Определить вероятности состояний цели после четырех выстрелов если матрица переходных вероятностей имеет вид:

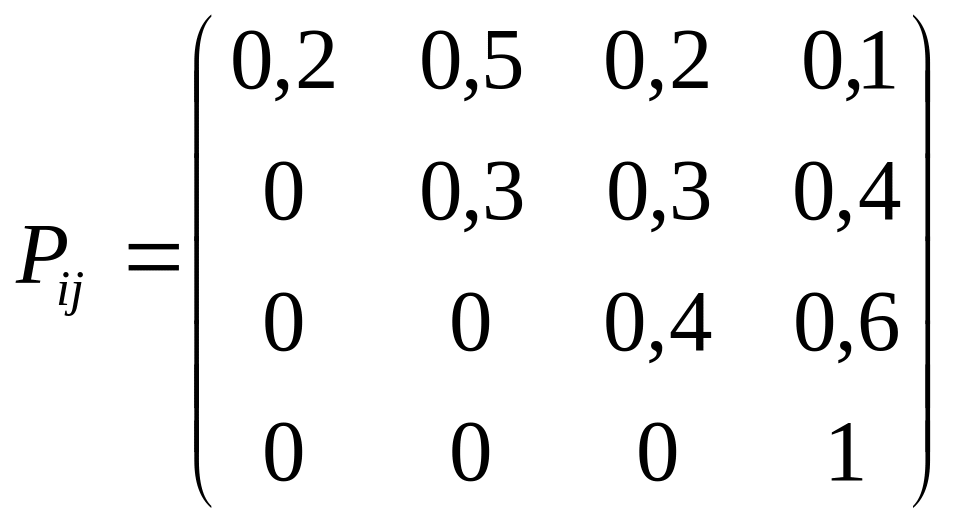
3.3.Непрерывные цепи Маркова

Марковский случайный процесс с дискретными состояниями и непрерывным временем называется непрерывной цепью Маркова при условии, что переход системы из состояния в состояние происходит не в фиксированные, а в случайные моменты времени.

Часто встречаются ситуации, которые указать заранее невозможно. Например, любая деталь или агрегат могут выходить из строя в любой, непредсказуемый заранее момент времени. Для описания таких систем и отдельных случаев можно использовать математический аппарат непрерывной цепи маркова.

Пусть система характеризуется n состояниями S₁, S₂, …, S_n, а переход из состояния в состояние может осуществляться в любой момент времени. Обозначим через P_i(t) вероятность того, что в момент времени t система S будет находиться в состоянии S_i (i = 1, 2, ..., n). Требуется определить для любого t вероятности состояний P₁(t), P₂(t), …, P_n(t). Очевидно, что

Для процесса с непрерывным временем вместо переходных вероятностей P_ij рассматриваются плотности вероятностей перехода _ij, представляющие coбой предел отношения вероятности перехода системы за время t из состояния S_i в состояние S_j к длине промежутка t:

(3.0)

где P_ij(t, t) – вероятность того, что система, пребывавшая в момент t в состоянии S_i, за время t перейдет из него в состояние S_j (при этом всегда i  j).

Если _ij = const, то процесс называется однородным, если плотность вероятности зависит от времени _ij = _ij(t), то процесс - неоднородный.

При рассмотрении непрерывных марковских процессов принято представлять переходы системы S из состояния в состояние как происходящие под влиянием некоторых потоков событий.

Плотность вероятности перехода интерпретируется как интенсивность _ij соответствующих потоков событий. Если все эти потоки пуассоновские, то процесс, протекающий в системе S, будет марковским.

При изучении марковских случайных процессов с дискретными состояниями и непрерывным временем в графе состояний над стрелками, ведущими из состояния S_i в S_j, проставляют соответствующие интенсивности _ij. Такой граф состояний называют размеченным.

Пусть система S имеет конечное число состояний S₁, …, S_n. Случайный процесс, протекающий в этой системе, описывается вероятностями состояний P₁(t), …, P_n(t), где P_i(t) - вероятность того, что система S в момент t находится в состоянии S_i. Для любого t

Вероятности состояний Р_i(t) находят путем решения системы дифференциальных уравнений (уравнении Колмогорова), имеющих вид

(3.0)

где i = 1, 2, …, n.

Величина _ijP_ij(t) называется потоком вероятности перехода из состояния S_i в S_j, причем интенсивность потоков _ij может зависеть от времени или быть постоянной.

Уравнения (3.3) составляют по размеченному графу состояний системы, пользуясь следующим мнемоническим правилом: производная вероятности каждого состояния равна сумме всех потоков вероятности, идущих из других состояний в данное состояние, минус сумма всех потоков вероятности, идущих из данного состояния в другие.

Чтобы решить систему дифференциальных уравнений (3.3), нужно задать начальное распределение вероятностей P₁(0), …, P_n(0). Для решения применяют численные методы.

3.4.Финальные вероятности состояний

Если процесс, протекающий в системе, длится достаточно долго, то имеет смысл говорить о предельном поведении вероятностей P_i(t) при . В некоторых случаях существуют финальные (предельные) вероятности состояний:

,

не зависящие от того, в каком состоянии система S находилась в начальный момент. Говорят, что в системе S устанавливается предельный стационарный режим, в ходе которою она переходит из состояния в состояние, но вероятности состояний Р_i уже не меняются. Система, для которой существуют финальные вероятности, называется эргодической, а соответствующий случайный процесс – эргодическим.

Финальные вероятности состояний (если они существуют) могут быть получены путем решения системы линейных алгебраических уравнений, которые получаются из дифференциальных уравнений Колмогорова, если приравнять производные к нулю, а вероятностные функции состояний Р₁(t), ..., Р_n(1) в правых частях уравнений (3.3) заменить соответственно на неизвестные финальные вероятности Р₁, ..., Р_n.

Таким образом, для системы S с n состояниями получается система n линейных однородных алгебраических уравнений с n неизвестными P₁, …, Р_n, которые можно найти с точностью до произвольного множителя. Для нахождения точного значения P₁, …, Р_n к уравнениям добавляют нормировочное условие Р₁ + Р₂ +...+ P_n = 1, пользуясь которым можно выразить любую из вероятностей Р_i через другие и отбросить одно из уравнений.

Пример 3. Имеется размеченный граф состояний системы S (рис. 3.4). Необходимо составить систему дифференциальных уравнений Колмогорова и записать начальные условия для решения этой системы, если известно, что в начальный момент система находилась в состоянии S₁.

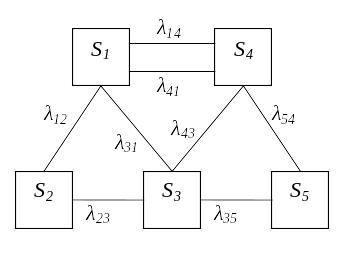
Рис. 3.6. Граф состояний системы

Решение

Согласно приведенному мнемоническому правилу, система дифференциальных уравнений Колмогорова имеет вид

Начальные условия при t = 0:

P₁ = 1; P₂ = P₃ = P₄ = P₅ = 0.

Рассмотрим, что произойдет с системой S, описываемой дифференциальными уравнениями Колмогорова, при . Известно, что в случае сообщающихся состояний функции P₁(t), P₂(t), …, P_n(t) стремятся к предельным (финальным) вероятностям состояний системы S. Финальные вероятности не зависят от времени. Поэтому в системе дифференциальных уравнений Колмогорова все левые части уравнений (производные) принимают равными нулю. При этом система дифференциальных уравнении превратится в систему линейных алгебраических уравнений.

Для нашего примера система будет иметь вид

Решая ее, с учетом условия Р₁ + Р₂ +.P₃ + P₄+ P₅ = 1, получим все предельные вероятности. Эти вероятности представляют собой не что иное, как среднее относительное время пребывания системы в данном состоянии.

Для существования финальных вероятностей одного условия _ij = const недостаточно, требуется выполнение еще некоторых условий, проверить которые можно по графу состояний, выделив в нем так называемые существенные и несущественные состояния.

Состояние S_i называется существенным, если нет другого состояния S_j, т.е. такого, что, перейдя однажды каким-то способом из S_i в S_j, система уже не может вернуться в S_i.

Все состояния, не обладающие таким свойством, называются несущественными.

Рассмотрим пример, представленный на рис. 3.5.

Рис. 3.7. Граф состояний системы S

Состояния S₁, S₂ и S₅ - несущественные, так как из S₁ можно уйти, например, в состояние S₂ и не вернуться, a из состояния S₂ - в состояние S₃ или S₄ и не вернуться; аналогично из состояния S₅ - в состояние S₆ и S₇. Состояния S₃, S₄, S₆ и S₇ - существенные состояния.

При конечном числе состояний для существования финальных вероятностей необходимо и достаточно, чтобы из каждого существенного состояния можно было (за какое-то число шагов) перейти в каждое другое существенное состояние.

Граф из примера рис. 3.5 этому условию не удовлетворяет, так как из существенного состояния S₄ нельзя перейти в существенное состояние S₇. Если система S имеет конечное число состояний S₁, S₂, ..., S_n, то для существования финальных вероятностей достаточно, чтобы из любого состояния системы можно было (за какое-то число шагов) перейти в любое другое состояние.

Если число состояний бесконечно, то это условие перестает быть достаточным, и существование финальных вероятностей зависит не только от графа состояний, но и от интенсивности _ij.

Задача 1. Построить систему дифференциальных уравнений для следующей системы:

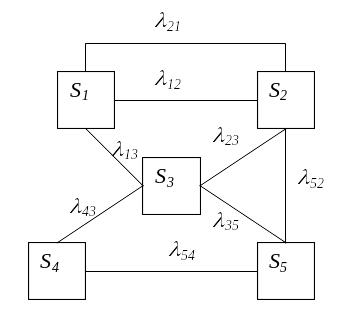
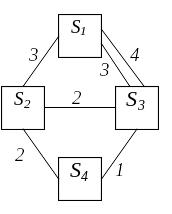
Задача 7. Физическая система S имеет возможные состояния: S₁, S₂, S₃, S₄. Вычислить предельные вероятности состояний.

3.5.Поток событий. Простейший поток и его свойства

При исследовании непрерывных марковских цепей, как было уже отмечено, часто бывает удобно представить переход системы из состояния в состояние как воздействие каких-то потоков событий (поток заявок на обслуживание, поток автомобилей, поток документов и т.п.).

Потоком событий называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени. Например, поток покупателей в магазин, поток машин на СТО, поток неисправностей у одного автомобиля и др.

Поток событий называется регулярным, если события следуют одно за другим через строго определенные промежутки времени. Такой поток сравнительно редко встречается на практике и не представляет особого интереса.

Различают следующие основные свойства, которыми могут обладать случайные потоки событий:

• стационарность;

• ординарность;

• отсутствие последействия.

Стационарность. Свойство стационарности проявляется в том, что вероятность попадания того или иного числа событии на участок времени  зависит только от длины участка и не зависит от расположения на оси 0t. Другими словами, стационарность означает неизменность вероятностного режима потока событий во времени. Поток, обладающий свойством стационарности, называют стационарным. Для стационарного потока среднее число событий, воздействующих на систему в течение единицы времени, остается постоянным (рис. 3.6). В большинстве случаях реальные потоки событий являются в действительности стационарными лишь на ограниченных участках времени. Например, поток автомобилей проезжающих по улице с 15 до 16 часов можно считать стационарным. Но, тот же поток в течение суток уже не будет стационарным (ночью поток машин, проезжающий по улице значительно меньше).

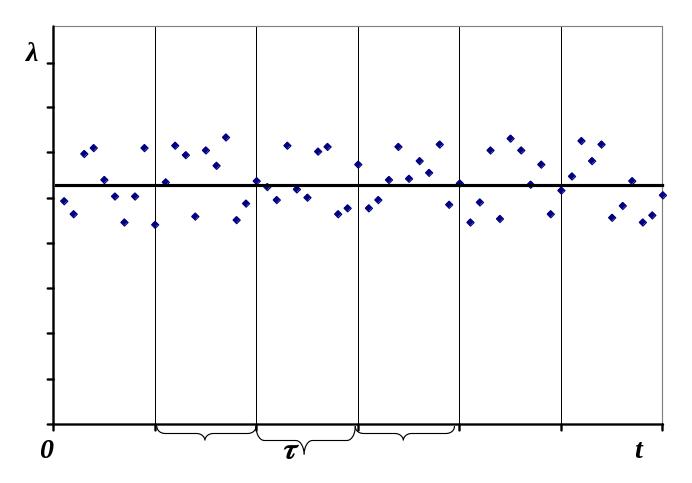
Рис. 3.8. График стационарного потока

Ординарность. Свойство ординарности потока присутствует, если вероятность попадания на элементарный участок времени двух и более событии пренебрежимо мала по сравнению с длиной этого участка. Свойство ординарности означает, что за малый промежуток времени практически невозможно появление более одного события. Поток, обладающий свойством ординарности, называют ординарным. Реальные потоки событий в различных производственно-экономических системах либо являются ординарными, либо могут быть достаточно просто приведены к ординарным.

Отсутствие последействия. Данное свойство потока состоит в том, что для любых непересекающихся участков времени количество событий, попадающих на один из них, не зависит от того, сколько событий попало на другие участки времени. Поток, обладающий свойством отсутствия последействия, называют потоком без последействия. Поток событий, одновременно обладающий свойствами стационарности, ординарности и отсутствия последействия, называется простейшим потоком событий.

Под интенсивностью потока понимают

где m(t, t + ) – среднее число событий в (t, t + ).

Для простейшего потока интенсивность  = const. Если поток событий не имеет последействия, ординарен, но не стационарен, то его называют нестационарным пуассоновским потоком, а его интенсивность зависит от времени, т. е.  = (t).

В пуассоновском потоке событий (стационарном и нестационарном) число событий потока, попадающих на любой участок, распределено по закону Пуассона:

m = 0, 1, …,

где P_m – вероятность попадания на участок m событий;

a – среднее число событий, приходящихся на участок.

Для простейшего потока a = , а для нестационарного пуассоновского потока

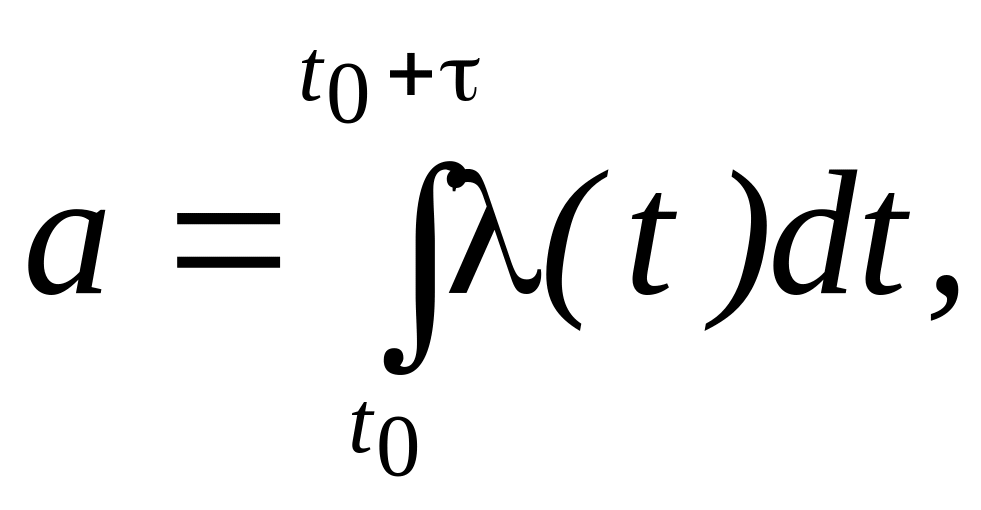
где  – длина участка времени;

t₀ – начало участка .

Отметим еще одно важное свойство простейшего потока событий. Промежуток времени t между соседними событиями распределен по показательному (экспоненциальному) закону, а его среднее значение и среднее квадратическое отклонение  равны, т. е.

где  – интенсивность потока.

Для нестационарного пуассоновского потока закон распределения промежутка t уже не является показательным, так как зависит от положения на оси 0t и вида зависимости (t). Однако для некоторых задач при сравнительно небольших изменениях (t) его можно приближенно считать показательным с интенсивностью , равной среднему значению (t).

Таким образом, для исследуемой системы S с дискретными состояниями и непрерывным временем переходы из состояния в состояние происходят под действием пуассоновских потоков событий с определенной интенсивностью _ij.

3.6.Процесс гибели и размножения

Рассмотрим еще одну типичную схему непрерывных марковских цепей - так называемую схему гибели и размножения, часто встречающуюся в разнообразных практических задачах.

Марковский процесс с дискретными состояниями S₀, S₁, ..., S_n называется процессом гибели и размножения, если все состояния можно вытянуть в одну цепочку, в которой каждое из средних состояний (S₁, S₂, ..., S_n-1) может переходить только в соседние состояния, которые, в свою очередь, переходят обратно, а крайние состояния (S₀ и S_n) переходят только в соседние состояния (рис. 3.7).

Название взято из биологических задач, где состояние популяции S_k означает наличие в ней k единиц особей.

Переход вправо связан с размножением единиц, а влево - с их гибелью.

Рис. 3.9. Граф состояний для процесса гибели и размножения

₀(t), ₁(t), ₂(t), …, _n(t) - интенсивности размножения;

₁(t), ₂(t), …, _n(t) - интенсивности гибели.

У  и μ индекс того состояния, из которою стрелка выходит.

С состоянием S_k связана неслучайная величина Х_k: если система S в момент времени t находится в состоянии S_k, то дискретная случайная величина X(t), связанная с функционированием системы, принимает значение k. Таким образом, получаем случайный процесс Х(t), который в случайные, заранее неизвестные моменты времени скачком изменяет свое состояние.

Марковским процессом гибели и размножения с непрерывным временем называется такой случайный процесс, который может принимать только целые неотрицательные значения. Изменения этого процесса могут происходить в любой момент времени, т. е. в любой момент времени он может либо увеличиться на единицу, либо уменьшиться на единицу, либо остаться неизменным.

В практике встречаются процессы чистого размножения и чистой гибели. Процессом чистого размножения называется такой процесс гибели и размножения, у которого интенсивности всех потоков гибели равны нулю; аналогично процессом чистой «гибели» называется такой процесс гибели и размножения, у которого интенсивности всех потоков размножения равны нулю.

Пример 1. Рассмотрим эксплуатацию моделей автомобилей одной марки в крупной транспортной фирме (на предприятии). Интенсивность поступления автомобилей на предприятие равна (t). Каждый поступивший на предприятие автомобиль списывается через случайное время T_c. Срок службы автомобиля  распределен по показательному закону с параметром . Процесс эксплуатации автомобилей является случайным процессом. A(t) - число автомобилей данной марки, находящихся в эксплуатации в момент t. Найдем одномерный закон распределения случайного процесса P_i(t) = P{A(t) = i}, если: 1) нет ограничений на число эксплуатируемых машин, 2) на предприятии может эксплуатироваться не более n автомобилей.

Решение.

1. Случайный процесс эксплуатации автомобилей есть процесс гибели и размножения, размеченный граф которого представлен на рис. 3.8.

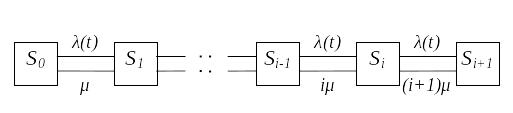
Рис. 3.10. Граф состояний

Система уравнений Колмогорова, соответствующая этому графу, имеет вид

(3.0)

где i = 1, 2, …

Если в начальный момент времени t = 0 на предприятии не было ни одного автомобиля, то решать эту систему уравнений нужно при начальных условиях P₀(0) = 1, P_i(0) = 0 (i = 1, 2, …). Если при t = 0 на предприятии было k автомобилей (k = 1, 2, ...), то начальные условия будут иметь вид

P_k(0) = 1, P_i(0) = 0 (i = 1, 2, …, i  k).

2. Если на предприятии может эксплуатироваться не более n автомобилей моделей одной марки, то имеет место процесс гибели и размножения с ограниченным числом состояний, размеченный граф которого представлен на рис. 3.9.

Рис. 3.11. Граф состояний

Система уравнений Колмогорова для размеченного графа (рис. 3.9) имеет вид (3.4).

Эту систему надо решать при начальных условиях, рассмотренных выше. Решения систем уравнений (3.4) и (3.5) являются одномерными законами распределения Р_i(t). Отыскание решений систем в общем виде при произвольном виде функции (t) представляет значительные трудности и не имеет практических приложении.

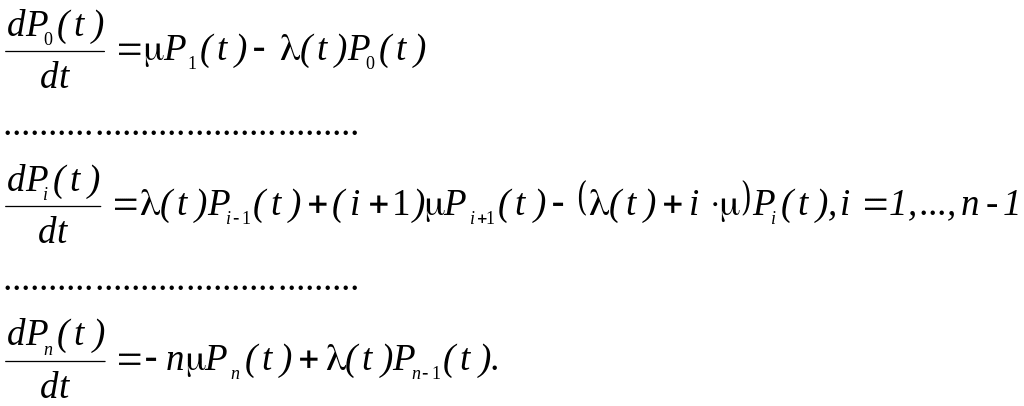(3.0)

При постоянных интенсивностях потоков гибели и размножения и конечном числе состояний будет существовать стационарный режим. Система S с конечным числом состояний (n + 1), в которой протекает процесс гибели и размножения с постоянными интенсивностями потоков гибели и размножения, является простейшей эргодической системой. Размеченный граф состояний для такой системы представлен на рис. 3.9.

Предельные (финальные) вероятности состояний для простейшего эргодического процесса гибели и размножения, находящегося в стационарном режиме, определяются по следующим формулам:

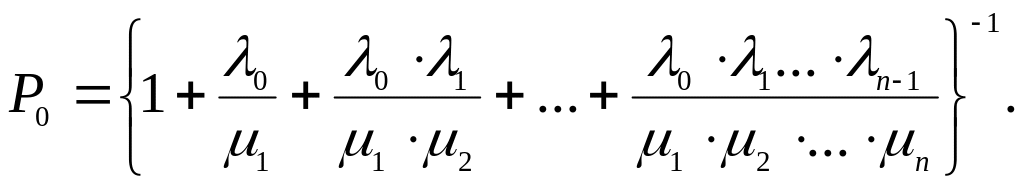(3.0)

(3.0)

Правило. Вероятность k-гo состояния в схеме гибели и размножения равна дроби, в числителе которой стоит произведение всех интенсивностей размножения, стоящих левее S_k, а в знаменателе - произведение всех интенсивностей гибели, стоящих левее S_k, умноженной на вероятность кранного левого состояния системы P₀.

В предыдущем примере для стационарного режима если интенсивность поступления автомобилей постоянная ((t) =  = const), то финальные вероятности состояний при условии, что нет ограничений на число автомобилей на предприятии, равны

(3.0)

. (3.0)

При этом математическое ожидание числа эксплуатируемых автомобилей равно его дисперсии:

M[A(t)] = D[A(t)] = /. (3.0)

Если существует ограничение по числу автомобилей на предприятии (не более n), то финальные вероятности можно записать в таком виде:

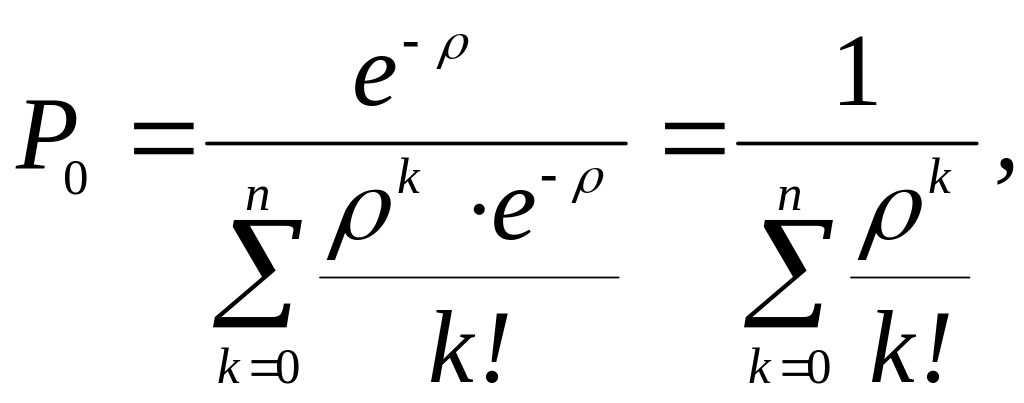(3.0)

где ρ = /.

(3.0)

где k = 0, 1, 2, ..., n.

Математическое ожидание числа эксплуатируемых автомобилей в стационарном режиме

(3.0)

Пример 2. В состав поточной лини входит четыре станка. Бригада в составе четырех человек обслуживающего персонала проводит профилактический ремонт каждого из них. Суммарный поток моментов окончания ремонтов для всей бригады - пуассоновский с интенсивностью (t). После окончания ремонта станок проверяется; с вероятностью Р он оказывается работоспособным (время проверки мало, и им можно пренебречь по сравнению со временем профилактики). Если станок оказывается неработоспособным, то вновь проводится его профилактика (время на которую не зависит от того, проводилась ли она ранее) и т. д. В начальный момент все станки нуждаются в профилактическом ремонте. Требуется:

1. Построить граф состояний для системы S (четыре станка).

2. Написать дифференциальные уравнения для вероятностей состояний.

3. Найти математическое ожидание числа станков M_, успению прошедших профилактику к моменту .

Решение.

Граф состояний показан на рис. 3.10, в котором:

S₀ – все четыре станка нуждаются в профилактическом ремонте;

S₁ – один станок успешно прошел профилактику, а три нуждаются в профилактическом ремонте;

S₂ – два станка успешно прошли профилактику, а два нуждаются в профилактическом ремонте;

S₃ – три станка успешно прошли профилактику, один нуждается в профилактическом ремонте;

S₄ – все четыре станка успешно прошли профилактику.

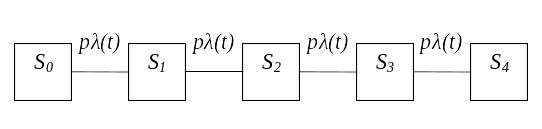
Рис. 3.12. Граф состояний системы

Каждый профилактический ремонт успешно заканчивается с вероятностью P, что равносильно P-преобразованию потока окончаний ремонтов, после которого он останется пуассоновским, но с интенсивностью P(t). В этом примере мы имеем дело с процессом чистого размножения с ограниченным числом состояний.

Уравнения Колмогорова имеют следующий вид:

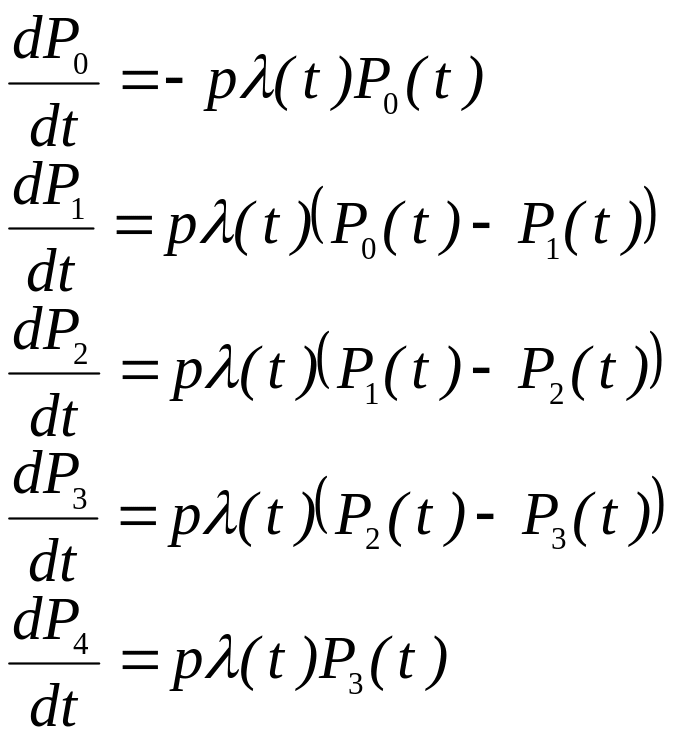
Начальные условия P₀(0) = 1, P₁(0) = … = P₄(0) = 0. При постоянной интенсивности (t) =  и вероятности состоянии определяются по следующим формулам:

Математическое ожидание числа дисков, успешно прошедших профилактику к моменту , равно

где n = 4.

Пример 3. Рассмотрим производство автомобилей на заводе. Поток производимых автомобилей - нестационарный пуассоновский с интенсивностью (t). Найдем одномерный закон распределения случайною процесса X(t) - число выпушенных автомобилей к моменту времени t, если в момент t = 0 начат выпуск автомобилей.

Решение

Очевидно, что здесь процесс чистого размножения без ограничения на число состояний, при этом _i(t) = (t), так как интенсивность выпуска автомобилей не зависит от того, сколько их уже выпушено. Граф состояний такого процесса показан на рис. 3.11.

Рис. 3.13. Граф состояний

Одномерный закон распределения случайного процесса Х(t) для графа, изображенного на рис. 3.11, определяется следующей системой уравнений Колмогорова:

Так как число выпушенных автомобилей X(t) на любой фиксированный момент t распределено по закону Пуассона с параметром

то

M[X(t)] = D[X(t)] = a(t).

Рассмотренный в этом примере процесс X(t) называется неоднородным процессом Пуассона. Если интенсивность (t) =  = const, то получим однородный процесс Пуассона. Для такого процесса при P₀(0) = 1, P_i(0) = 0 (i > 0)

Характеристиками процесса Пуассона будут

M[X(t)] = D[X(t)] = t.

Задача 1. Имеется прибор, который состоит из четырех узлов; поток отказов – простейший, среднее время безотказной работы каждого узла равно 11 час. Отказавший узел сразу начинает ремонтироваться; среднее время ремонта узла равно 2 час. (поток восстановления простейший). Найти среднюю производительность прибора, если при четырех работающих узлах она равна 100%, при трех 60%, при двух и менее прибор вообще не работает.

3.7.Циклический процесс

Марковский случайный процесс, протекающий в системе, называется циклическим, если состояния связаны между собой в кольцо (цикл) с односторонними переходами (рис. 3.12).

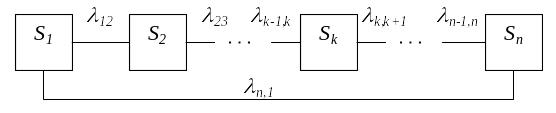
Рис. 3.14. Граф состояний циклического процесса

Для более удобного понимания процесса целесообразно перейти от параметра λ_ij к среднему времени ( _i) пребывания системы в данном состоянии S_i (i=1, …, n). При этом формула для нахождения финальных вероятностей системы будет равна:

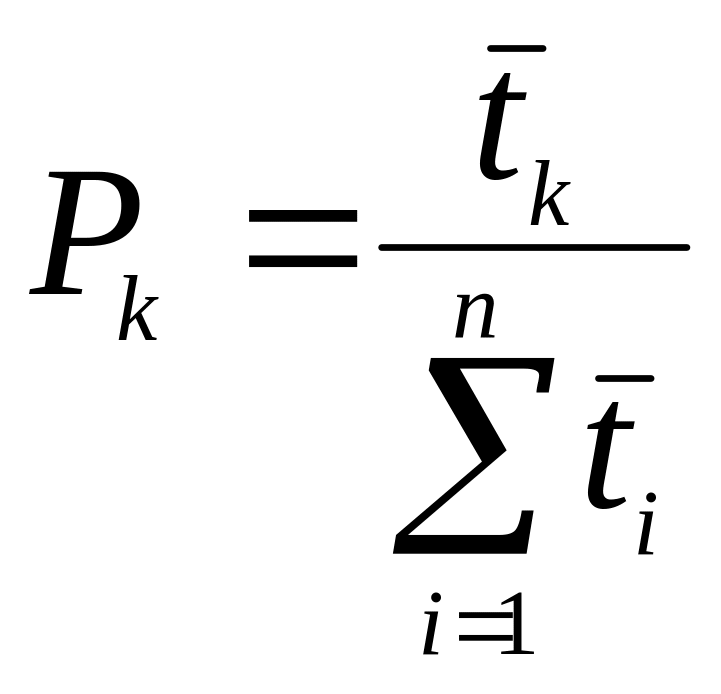(k=1, …, n),

где , .

Предельные вероятности состояний в циклической схеме относится как средние времена пребывания системы подряд в каждом из состояний.

Задача 1. Имеется устройство, состояния которого меняются с течением времени:

S₁– исправно.

S₂ – неисправно, ведется поиск неисправности.

S₃ – ремонт.

Известно, что среднее время безотказной работы устройства – 28 дней. Среднее время поиска неисправности – 1,5 дня. Среднее время ремонта устройства составляет 2,1 день, после чего устройство опять становится исправным.

Найти предельные вероятности состояний устройства.

4.Компоненты и классификация моделей массового обслуживания

Предметом теории массового обслуживания является установление зависимости между факторами, определяющими функциональные возможности системы массового обслуживания, и эффективностью ее функционирования. В большинстве случаев все параметры, описывающие системы массового обслуживания, являются случайными величинами или функциями, поэтому эти системы относятся к стохастическим системам.

Системы массового обслуживания - это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания, а если все каналы заняты, то заявки образуют очередь.

С позиции моделирования процесса массового обслуживания ситуации, когда образуются очереди заявок (требований) на обслуживание, возникают следующим образом. Поступив в обслуживающую систему, требование присоединяется к очереди других (ранее поступивших) требований. Канал обслуживания выбирает требование из находящихся в очереди, с тем, чтобы приступить к его обслуживанию. После завершения процедуры обслуживания очередного требования канал обслуживания приступает к обслуживанию следующего требования, если таковое имеется в блоке ожидания. Цикл функционирования системы массового обслуживания подобного рода повторяется многократно в течение всего периода работы обслуживающей системы. При этом предполагается, что переход системы на обслуживание очередного требования после завершения обслуживания предыдущего требования происходит мгновенно, в случайные моменты времени.

Примерами систем массового обслуживания могут служить:

• посты технического обслуживания автомобилей;

• посты ремонта автомобилей;

• персональные компьютеры, обслуживающие поступающие заявки или требования на решение тех или иных задач;

• станции технического обслуживания автомобилей;

• аудиторские фирмы;

• отделы налоговых инспекций, занимающиеся приемкой и проверкой текущей отчетности предприятий;

• телефонные станции и т. д.

Основными компонентами системы массового обслуживания любого вида являются (рис. 4.1):

• входной поток поступающих требований или заявок на обслуживание;

• очередь;

• обслуживающие аппараты, механизм обслуживания;

• выходящий поток.

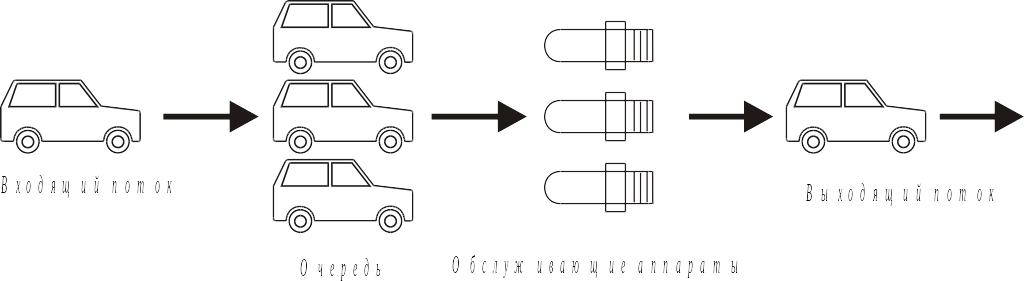
Рис. 4.15. Основные компоненты системы массового обслуживания

Раскроем содержание каждого из указанных выше компонентов.

Входной поток требований. Для описания входного потока требуется задать вероятностный закон, определяющий последовательность моментов поступления требований на обслуживание и указать количество таких требований в каждом очередном поступлении. При этом, как правило, оперируют понятием «вероятностное распределение моментов поступления требований». Здесь могут поступать как единичные, так и групповые требования (требования поступают группами в систему). В последнем случае обычно речь идет о системе обслуживания с параллельно-групповым обслуживанием.

Очередь образуется в том случае, когда пропускная способность обслуживающих аппаратов недостаточна по отношению к входящему потоку требований.

Кроме того существует такое понятие как дисциплина очереди – это важный компонент системы массового обслуживания, он определяет принцип, в соответствии с которым поступающие на вход обслуживающей системы требования подключаются из очереди к процедуре обслуживания. Чаще всего используются дисциплины очереди, определяемые следующими правилами:

• первым пришел - первый обслуживаешься;

• пришел последним - обслуживаешься первым;

• случайный отбор заявок;

• отбор заявок по критерию приоритетности (часть требований имеет преимущество перед другими);

Механизм обслуживания определяется характеристиками самой процедуры обслуживания и структурой обслуживающей системы. К характеристикам процедуры обслуживания относятся: продолжительность процедуры обслуживания и количество требований, удовлетворяемых в результате выполнения каждой такой процедуры. Для аналитического описания характеристик процедуры обслуживания оперируют понятием «вероятностное распределение времени обслуживания требований».

Следует отметить, что время обслуживания заявки зависит от характера самой заявки или требований клиента и от состояния и возможностей обслуживающей системы. В ряде случаев приходится также учитывать вероятность выхода обслуживающего прибора по истечении некоторого ограниченного интервала времени.

Структура обслуживающей системы определяется количеством и взаимным расположением каналов обслуживания (механизмов, приборов и т. п.). Прежде всего, следует подчеркнуть, что система обслуживания может иметь не один канал обслуживания, а несколько; система такого рода способна обслуживать одновременно несколько требований. В этом случае все каналы обслуживания предлагают одни и те же услуги, и, следовательно, можно утверждать, что имеет место параллельное обслуживание.

Система обслуживания может состоять из нескольких разнотипных каналов обслуживания, через которые должно пройти каждое обслуживаемое требование, т. е. в обслуживающей системе процедуры обслуживания требований реализуются последовательно. Механизм обслуживания определяет характеристики выходящего (обслуженного) потока требований.

Выходящий поток также играет важную роль, так как он сам может образовывать входящий поток в другую систему массового обслуживания. Кроме обслуженных заявок выходящий поток может включать и не обслуженные (например, невозможность устранения определенного вида отказов).

Рассмотрев основные компоненты систем обслуживания, можно констатировать, что функциональные возможности любой системы массового обслуживания определяются следующими основными факторами:

• вероятностным распределением моментов поступлений заявок на обслуживание (единичных или групповых);

• вероятностным распределением времени продолжительности обслуживания;

• конфигурацией обслуживающей системы (параллельное, последовательное или параллельно-последовательное обслуживание);

• количеством и производительностью обслуживающих каналов;

• дисциплиной очереди;

• мощностью источника требований.

В качестве основных критериев эффективности функционирования систем массового обслуживания в зависимости от характера решаемой задачи могут выступать:

• вероятность немедленного обслуживания поступившей заявки;

• вероятность отказа в обслуживании поступившей заявки;

• относительная и абсолютная пропускная способность системы;

• средний процент заявок, получивших отказ в обслуживании;

• среднее время ожидания в очереди;

• средняя длина очереди;

• средний доход от функционирования системы в единицу времени и т.п.

Случайный характер потока заявок (требований), а также, в общем случае, и длительности обслуживания приводит к тому, что в системе массового обслуживания происходит случайный процесс. По характеру случайного процесса, происходящего в системе массового обслуживания (СМО), различают системы Марковские и немарковские. В Марковских системах входящий поток требований и выходящий поток обслуженных требований (заявок) являются пуассоновскими. Пуассоновские потоки позволяют легко описать и построить математическую модель системы массового обслуживания. Данные модели имеют достаточно простые решения, поэтому большинство известных приложений теории массового обслуживания используют Марковскую схему. В случае немарковских процессов задачи исследования систем массового обслуживания значительно усложняются и требуют применения статистического моделирования, численных методов с использованием ЭВМ.

Независимо от характера процесса, протекающего в системе массового обслуживания, различают два основных вида СМО:

• системы с отказами, в которых заявка, поступившая в систему в момент, когда все каналы заняты, получает отказ и сразу же покидает очередь;

• системы с ожиданием (очередью), в которых заявка, поступившая в момент, когда все каналы обслуживания заняты, становится в очередь и ждет, пока не освободится один из каналов.

Системы массового обслуживания с ожиданием делятся на системы с ограниченным ожиданием и системы с неограниченным ожиданием.

В системах с ограниченным ожиданием может ограничиваться:

• длина очереди;

• время пребывания в очереди.

В системах с неограниченным ожиданием заявка, стоящая в очереди, ждет обслуживание неограниченно долго, т.е. пока не подойдет очередь.

Все системы массового обслуживания различают по числу каналов обслуживания:

• одноканальные системы;

• многоканальные системы.

Приведенная классификация СМО является условной. На практике чаще всего системы массового обслуживания выступают в качестве смешанных систем. Например, заявки ожидают начала обслуживания до определенного момента, после чего система начинает работать как система с отказами.

5.Определение характеристик систем массового обслуживания

5.1.Одноканальная модель смо с пуассоновским входным потоком с экспоненциальным распределением длительности обслуживания

Простейшей одноканальной моделью с вероятностными входным потоком и процедурой обслуживания является модель, характеризуемая показательным распределением как длительностей интервалов между поступлениями требований, так и длительности обслуживания. При этом плотность распределения длительностей интервалов между поступлениями требований имеет вид

f₁(t) = e^-t, (5.0)

где  – интенсивность поступления заявок в систему.

Плотность распределения длительностей обслуживания:

f₂(t) = e^-t, (5.0)

где  – интенсивность обслуживания.

Потоки заявок и обслуживаний простейшие.

Пусть система работает с отказами. Необходимо определить, абсолютную и относительную пропускную способность системы.

Представим данную систему массового обслуживания в виде графа (рис. 2.1), у которого имеются два состояния: S₀ – канал свободен (ожидание); S₁ – канал занят (идет обслуживание заявки).

Рис. 5.16. Граф состояний одноканальной СМО с отказами

Обозначим вероятности состояний:

P₀(t) – вероятность состояния «канал свободен»;

P₁(t) – вероятность состояния «канал занят».

По размеченному графу состояний (рис. 5.1) составим систему дифференциальных уравнений Колмогорова для вероятностей состояний:

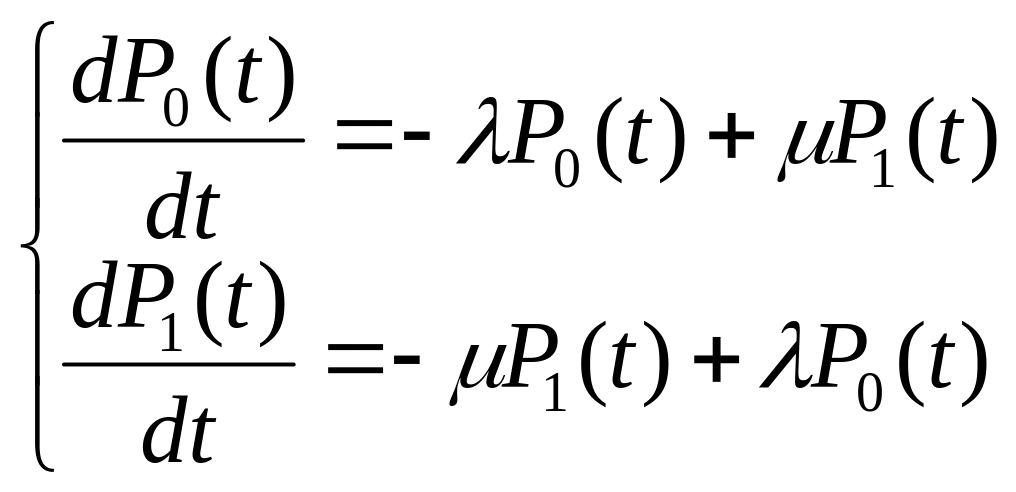. (5.0)

Система линейных дифференциальных уравнений (3) имеет решение с учетом нормировочного условия P₀(t) + P₁(t) = 1. Решение данной системы называется неустановившимся, поскольку оно непосредственно зависит от t и выглядит следующим образом:

(5.0)

P1(t) = 1 – P0(t). (5.0)

Нетрудно убедиться, что для одноканальной СМО с отказами вероятность P₀(t) есть не что иное, как относительная пропускная способность системы q.

Действительно, P₀ – вероятность того, что в момент t канал свободен и заявка, пришедшая к моменту t, будет обслужена, а следовательно, для данного момента времени t среднее отношение числа обслуженных заявок к числу поступивших также равно P₀(t),т.е.

q = P₀(t). (5.0)

По истечении большого интервала времени (при ) достигается стационарный (установившийся) режим:

, (5.0)

где q – относительная пропускная способность(доля обслуженных заявок от общего их количества, поступающего в систему).

Зная относительную пропускную способность, легко найти абсолютную. Абсолютная пропускная способность А – среднее число заявок, которое может обслужить система массового обслуживания в единицу времени:

(5.0)

Вероятность отказа в обслуживании заявки будет равна вероятности состояния «канал занят»:

(5.0)

Данная величина P_отк может быть интерпретирована как средняя доля не обслуженных заявок среди поданных.

Пример 1. Пусть одноканальная СМО с отказами представляет собой один пост ежедневного обслуживания (ЕО) для мойки автомобилей. Заявка - автомобиль, прибывший в момент, когда пост занят, - получает отказ в обслуживании. Интенсивность потока автомобилей  = 1,0 (автомобиль в час). Средняя продолжительность обслуживания t_об=1,8 часа. Поток автомобилей и поток обслуживаний являются простейшими. Требуется определить в установившемся режиме предельные значения: относительной пропускной способности q; абсолютной пропускной способности А; вероятности отказа Р_отк. Сравните фактическую пропускную способность СМО с номинальной, которая была бы, если бы каждый автомобиль обслуживался точно 1,8 часа и автомобили следовали один за другим без перерыва.

Решение

1. Определим интенсивность потока обслуживания:

авто/час.

2. Вычислим относительную пропускную способность:

Величина q означает, что в установившемся режиме система будет обслуживать примерно 35% прибывающих на пост ЕО автомобилей.

3. Абсолютную пропускную способность определим по формуле:

А = q = 10,356 = 0,356 авто.

Это означает, что система (пост ЕО) способна осуществить в среднем 0,356 обслуживания автомобилей в час.

4. Вероятность отказа:

P_отк = 1 - q = 1 - 0,356 = 0,644.

Это означает, что около 65% прибывших автомобилей на пост ЕО получат отказ в обслуживании.

5. Определим номинальную пропускную способность системы:

(автомобилей в час).

Оказывается, что А_ном в 1,5 раза (0,555/0,356  1,5) больше, чем фактическая пропускная способность, вычисленная с учетом случайного характера потока заявок и времени обслуживания.

Задача 1. Известно, что заявки на телефонные переговоры в телефонном ателье поступают с интенсивностью, равной 90 заявок в час, а средняя продолжительность разговора по телефону t_o6=2 мин.

Определить показатели эффективности работы СМО (телефонной связи) при наличии одного телефонного номера.

5.2.Одноканальная модель смо с ожиданием

Система массового обслуживания имеет один канал. Входящий поток заявок на обслуживание - простейший поток с интенсивностью . Интенсивность потока обслуживания равна  (т. е. в среднем непрерывно занятый канал будет выдавать  обслуженных заявок). Длительность обслуживания - случайная величина, подчиненная показательному закону распределения. Поток обслуживаний является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.

Предположим, что независимо от того, сколько требований поступает на вход обслуживающей системы, данная система (очередь + обслуживаемые клиенты) не может вместить более N требований (заявок), т. е. клиенты, не попавшие в ожидание, вынуждены обслуживаться в другом месте. Наконец, источник, порождающий заявки на обслуживание, имеет неограниченную (бесконечно большую) емкость.

Граф состояний СМО в этом случае имеет вид, показанный на рис. 5.2.

Рис. 5.17. Граф состояний одноканальной СМО с ожиданием (схема гибели и размножения)

Состояния СМО имеют следующую интерпретацию:

S₀ –­­ «канал свободен»;

S₁ ­–­­­ «канал занят» (очереди нет);

S₂ – «канал занят» (одна заявка стоит в очереди);

S_k – «канал занят» (k-1 заявок стоит в очереди);

S_m+1 – «канал занят» (m заявок стоит в очереди).

Стационарный процесс в данной системе будет описываться следующей системой алгебраических уравнений:

Пользуясь уравнениями для процесса гибели и размножения получим:

(5.0)

где – приведенная интенсивность (плотность) потока;

Тогда вероятность что занят 1 канал и k-1 мест в очереди:

Следует отметить, что выполнение условия стационарности < 1 для данной СМО не обязательно, поскольку число допускаемых в обслуживающую систему заявок контролируется путем введения ограничения на длину очереди (которая не может превышать m), а не соотношением между интенсивностями входного потока, т. е. не отношением .

Определим характеристики одноканальной СМО с ожиданием и ограниченной длиной очереди, равной m:

вероятность отказа в обслуживании заявки;

; (5.0)

относительная пропускная способность системы:

; (5.0)

абсолютная пропускная способность:

А = q; (5.0)

среднее число заявок, находящихся в очереди:

; (5.0)

среднее число заявок, находящихся под обслуживанием:

(5.0)

среднее число заявок, находящихся в системе(связанных с СМО):

; (5.0)

среднее время пребывания заявки в системе:

Т_сист.= Т_ож. + t_об; (5.0)

средняя продолжительность пребывания клиента (заявки) в очереди:

. (5.0)

Если имеется неограниченное число мест ожидания в очереди m, то вышеуказанные формулы справедливы только при ρ < 1, так как при ρ 1 нет установившегося режима (очередь неограниченно растет) и при q=1, A=λq=λ.

Рассмотрим пример одноканальной СМО с ожиданием.

Пример. Специализированный пост диагностики представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики, ограниченно и равно 3. Если все стоянки заняты, т. е. в очереди уже находится три автомобиля, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по закону Пуассона и имеет интенсивность  = 0,85 (автомобиля в час). Время диагностики автомобиля распределено по показательному закону и в среднем равно 1,05 час.

Требуется определить вероятностные характеристики поста диагностики, работающего в стационарном режиме.

Решение.

Интенсивность обслуживания автомобилей:

(авто/час)

Приведенная интенсивность потока автомобилей определяется как отношение интенсивностей  и , т. е.

Вычислим предельные вероятности системы:

Вероятность отказа в обслуживании автомобиля:

P_отк = P₄ = ⁴P₀  0,158.

Значит 15,8% автомобилей получат отказ в обслуживании так как не будет свободных постов и мест в очереди.

Относительная пропускная способность поста диагностики:

q = 1 - P_отк= 1 - 0,158 = 0,842.

Это означает что обслуживается в среднем 82,4% автомобилей.

Абсолютная пропускная способность поста диагностики

А = q = 0,85  0,842 = 0,716 (автомобиля в час).

Среднее число автомобилей, находящихся в системе – среднее число заявок, находящихся в очереди плюс среднее число заявок, находящихся под обслуживанием:

Среднее время пребывания автомобиля в системе складывается из среднего времени ожидания в очереди и продолжительности обслуживания (если заявка принята к обслуживанию):

Работу рассмотренного поста диагностики можно считать удовлетворительной, так как пост диагностики не обслуживает автомобили в среднем в 15,8% случаев (Р_отк = 0,158).

Задача 1. Автозаправочная станция (АЗС) представляет собой СМО с одним каналом обслуживания (одной колонкой). Площадка при станции допускает пребывание в очереди на заправку не более трех машин одновременно (m = 6). Если в очереди уже находится 6 машин, очередная машина, прибывшая к станции, в очередь не становится, а проезжает мимо. Поток машин, прибывающих для заправки, имеет интенсивность λ = 0,95 (машина в минуту). Процесс заправки продолжается в среднем 1,25 мин. Определить:

• вероятность отказа;

• относительную и абсолютную пропускную способности СМО;

• среднее число машин, ожидающих заправки;

• среднее число машин, находящихся на АЗС (включая и обслуживаемую);

• среднее время ожидания машины в очереди;

• среднее время пребывания машины на АЗС (включая обслуживание).

• доход АЗС за 10 часов при стоимости литра бензина равной 20 руб. и среднем объеме одной заправки автомобиля равной 7,5 литров.

Задача 2. Вспомним о ситуации, рассмотренной в задаче 1, где речь идет о функционировании поста диагностики. Пусть рассматриваемый пост диагностики располагает неограниченным количеством площадок для стоянки прибывающих на обслуживание автомобилей, т. е. длина очереди не ограничена.

Требуется определить финальные значения следующих вероятностных характеристик:

• вероятности состояний системы (поста диагностики);

• среднее число автомобилей, находящихся в системе (на обслуживании и в очереди);

• среднюю продолжительность пребывания автомобиля в системе (на обслуживании и в очереди);

• среднее число автомобилей в очереди на обслуживании;

• среднюю продолжительность пребывания автомобиля в очереди.

Задача 3. На железнодорожную сортировочную горку прибывают составы с интенсивностью λ = 2 (состава в час). Среднее время, в течение которого горка обрабатывает состав, равно 0,4 часа. Составы, прибывшие в момент, когда горка занята, становятся в очередь и ожидают в парке прибытия, где имеются три запасных пути, на каждом из которых может ожидать один состав. Состав, прибывший в момент, в очередь на внешний путь. Все потоки событий – простейшие. Найти:

• среднее число составов, ожидающих очереди (как в парке прибытия, так и вне его);

• среднее время ожидания состава в парке прибытия и на внешних путях;

• среднее время нахождения состава на сортировочной станции (включая ожидание и обслуживание);

• вероятность того, что прибывший состав займет место на внешних путях.

5.3.Многоканальная модель смо с отказами

В подавляющем большинстве случаев на практике системы массового обслуживания являются многоканальными, и, следовательно, модели с n обслуживающими каналами (где n > 1) представляют несомненный интерес.

Процесс массового обслуживания, описываемый данной моделью, характеризуется интенсивностью входного потока , при этом параллельно может обслуживаться не более n клиентов (заявок). Средняя продолжительность обслуживания одной заявки равняется 1/. Входной и выходной потоки являются пуассоновскими. Режим функционирования того или иного обслуживающего канала не влияет на режим функционирования других обслуживающих каналов системы, причем длительность процедуры обслуживания каждым из каналов является случайной величиной, подчиненной экспоненциальному закону распределения. Конечная цель использования n параллельно включенных обслуживающих каналов заключается в повышении (по сравнению с одноканальной системой) скорости обслуживания требований за счет обслуживания одновременно n клиентов.

Граф состояний многоканальной системы массового обслуживания с отказами имеет вид, показанный на рис. 2.3.

Рис. 5.18. Граф состояний многоканальной СМО с отказами

Состояния данной СМО имеют следующую интерпретацию:

S₀ – все каналы свободны;

S₁ – занят один канал, остальные свободны;

S_k – заняты ровно k каналов, остальные свободны;

S_n – заняты все n каналов, заявка получает отказ в обслуживании.

Формулы для вычисления вероятностей P_k называются формулами Эрланга.

Определим вероятностные характеристики функционирования многоканальной СМО с отказами в стационарном режиме:

вероятность того, что все посты свободны:

; (5.0)

вероятность отказа:

, (5.0)

так как заявка получает отказ, если приходит в момент, когда все каналы заняты. Величина P_отк характеризует полноту обслуживания входящего потока;

вероятность того, что заявка будет принята к обслуживанию (она же - относительная пропускная способность системы q) дополняет Р_отк до единицы:

; (5.0)

абсолютная пропускная способность:

A = q; (5.0)

среднее число каналов, занятых обслуживанием следующее:

(5.0)

Величина M[n] характеризует степень загрузки СМО.

Пример. Пусть n-канальная СМО представляет собой вычислительный центр (ВЦ) с тремя (n = 3) взаимозаменяемыми ЭВМ для решения поступающих задач. Поток задач, поступающих на ВЦ, имеет интенсивность  = 1 задаче в час. Средняя продолжительность обслуживания = 1,8 час. Поток заявок на решение задач и поток обслуживания этих заявок являются простейшими.

Требуется вычислить финальные значения:

• вероятности состояний ВЦ;

• вероятности отказа в обслуживании заявки;

• относительной пропускной способности ВЦ;

• абсолютной пропускной способности ВЦ;

• среднего числа занятых ПЭВМ на ВЦ.

Определите, сколько дополнительно надо приобрести ПЭВМ, чтобы увеличить пропускную способность ВЦ в 2 раза.

Решение

1. Определим параметр . потока обслуживаний:

з/час

2. Приведенная интенсивность потока заявок

3. Предельные вероятности состояний найдем по формулам Эрланга (27):

4. Вероятность отказа в обслуживании заявки

P_отк = P₃ = 0,180.

5. Относительная пропускная способность ВЦ

q = 1 – Pотк = 1 – 0,180 = 0,820.

6. Абсолютная пропускная способность ВЦ

А = q = 10,820 = 0,820. з/час.

7. Среднее число занятых каналов – ПЭВМ

Таким образом, при установившемся режиме работы СМО в среднем будет занято 1,5 компьютера из трех - остальные полтора будут простаивать. Работу рассмотренного ВЦ вряд ли можно считать удовлетворительной, так как центр не обслуживает заявки в среднем в 18% случаев (Р₃ = 0,180). Очевидно, что пропускную способность ВЦ при данных  и  можно увеличить только за счет увеличения числа ПЭВМ.

Определим, сколько нужно использовать ПЭВМ, чтобы сократить число не обслуженных заявок, поступающих на ВЦ, в 10 раз, т.е. чтобы вероятность отказа в решении задач не превосходила 0,0180. Для этого используем формулу (5.20):

Составим следующую таблицу:

Анализируя данные таблицы, следует отметить, что расширение числа каналов ВЦ при данных значениях  и , 6 единиц ПЭВМ позволит обеспечить удовлетворение заявок на решение задач на 99,22%, так как при n = 6 вероятность отказа в обслуживании (P_отк) составляет 0,0078.

Задача 1. Исследуется работа станции технического обслуживания автомобилей с отказами. Станция имеет в своем распоряжении четыре подъемника. На станцию поступает простейший поток заявок с интенсивностью 3 автомобилей в час. Время обслуживания распределено по показательному закону и характеризуется средней продолжительностью 2 часа на автомобиль. Требуется построить граф состояний и определить числовые характеристики функционирования станции за восьмичасовой рабочий день.

Задача 2. В зону текущего ремонта в среднем поступает 8 единиц техники в день. Известно, что отказы распределены следующим образом: 35% – двигатель и трансмиссия, 40% –подвеска, 25% – прочие отказы. Зона в своем распоряжении имеет 3 поста, по одному на каждый вид отказа. Известно, что средняя продолжительность устранения отказов распределена так: двигатель и трансмиссия – 5 часов, подвеска – 3,5 часа, прочие отказы – 2 часа. Определить оптимальное число постов текущего ремонта с учетом того, чтобы отказов было не более 5%.

Задача 3. Исследуется функционирование станции мойки автомобилей, работающей с отказами. На станцию поступает простейший поток автомобилей с интенсивностью 3 автомобиля в час. Время обслуживания распределено по показательному закону и характеризуется временем равным 20 минут. Требуется определить число мест мойки, при котором только 8% машин получат отказы.

5.4.Многоканальная модель смо с ожиданием

Процесс массового обслуживания при этом характеризуется следующим: входной и выходной потоки являются пуассоновскими с интенсивностями  и  соответственно; параллельно обслуживаться могут не более n клиентов. Система имеет n каналов обслуживания. Средняя продолжительность обслуживания одного клиента равна 1/.

Рис. 5.19. Граф состояний многоканальной СМО с ожиданием

Состояния системы будем нумеровать по числу заявок, связанных с системой:

S₀ – все каналы свободны;

S₁ – занят один канал, остальные свободны;

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

S_k – заняты k каналов, остальные свободны;

. . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . .

S_n – заняты все n каналов;

S_n+1 – заняты все n каналов; одна заявка стоит в очереди;

. . . . . . . . . . .. . . . .. . . .. . . . . . . .. . . . . . . . . . . . . . . . . . .

S_n+r – заняты все n каналов, r заявок стоят в очереди;

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

S_n+m – заняты все n каналов, m заявок стоят в очереди.

По стрелкам слева направо систему переводит всегда один и тот же поток заявок с интенсивностью λ, по стрелкам справа налево систему переводит поток обслуживаний, интенсивность которого равна µ, умноженному на число занятых каналов.

Решение будет действительным, если выполняется следующее условие: .

Вероятностные характеристики функционирования в стационарном режиме многоканальной СМО с ожиданием и неограниченной очередью определяются по следующим формулам.

Вероятность того, что все посты свободны:

при неограниченной длине очереди:

(5.0)

при длине очереди ограниченной числом m:

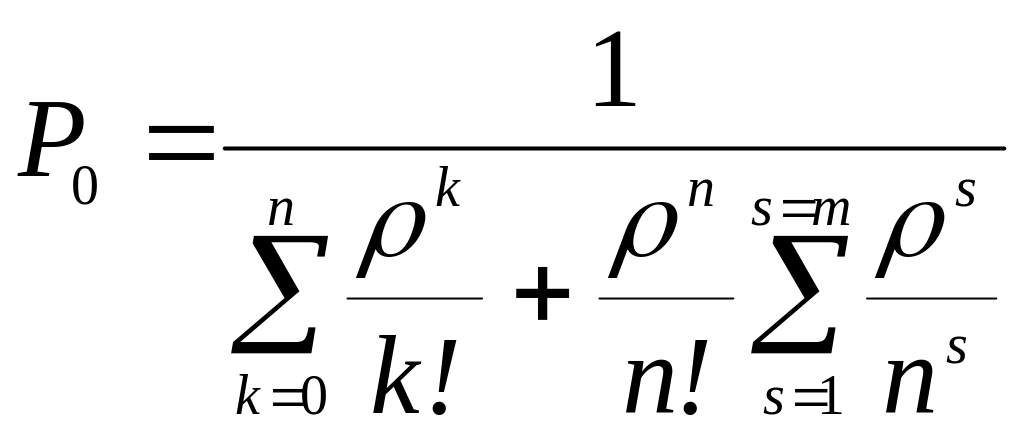; (5.0)

вероятность отказа система (все посты заняты, все места в очереди заняты):

; (5.0)

вероятность того, что занято k постов и r постов ожидания:

; (5.0)

; (5.0)

среднее число заявок в очереди:

, (5.0)

где ;

среднее число занятых каналов:

(5.0)

складывая среднее число заявок в очереди и среднее число занятых каналов , получим среднее число заявок, связанных с системой:

; (5.0)

среднее время ожидания заявки в очереди:

; (5.0)

средняя продолжительность пребывания заявки в системе:

t_сист = +1/.. (5.0)

Рассмотрим пример многоканальной системы массового обслуживания с ожиданием.

Пример. Механическая мастерская завода с тремя постами (каналами) выполняет ремонт малой механизации. Поток неисправных механизмов, прибывающих и мастерскую, - пуассоновский и имеет интенсивность  = 2,5 механизма в сутки, среднее время ремонта одного механизма распределено по показательному закону и равно t_об = 0,5 суток. Предположим, что другой мастерской на заводе нет, и, значит, очередь механизмов перед мастерской может расти практически неограниченно.

Требуется вычислить следующие предельные значения вероятностных характеристик системы:

• вероятности состоянии системы;

• среднее число заявок в очереди на обслуживание;

• среднее число находящихся в системе заявок;

• среднюю продолжительность пребывания заявки в очереди;

• среднюю продолжительность пребывания заявки в системе.

Решение

Так как то каждая заявка будет рано или поздно обслужена: Р_отк=0, q=1,A=λq=λ.

1. Определим параметр потока обслуживаний

2. Приведенная интенсивность потока заявок

 =  /  = 2,5 / 2,0 = 1,25,

при этом  / (n) = 2,5 / (23) = 0,41.

Поскольку /(n)<1, то очередь не растет безгранично, и в системе наступает предельный стационарный режим работы.

3. Вычислим вероятности состояний системы:

4. Вероятность отсутствия очереди у мастерской

P_от.оч = P₀ + P₁ + P₂ + P₃  0,285 + 0,356 + 0,223 + 0,092 = 0,987.

5. Среднее число заявок в очереди на обслуживание при

.

6. Среднее число находящихся в системе заявок

.

7. Средняя продолжительность пребывания механизма в очереди на обслуживание

Т_ож=0,113/2,5=0,0452 суток.

8. Средняя продолжительность пребывания механизма в мастерской (системе)

Т_сист=0,0452+0,5=0,5452 суток.

Задача 1. Автозаправочная станция (АЗС) с двумя колонками (n = 2) предназначена для обслуживания машин. Поток машин, прибывающих на АЗС, имеет интенсивность λ = 2 (машины в минуту); среднее время обслуживания одной машины 2 мин .

Площадка у АЗС может вместить очередь не более m = 3 (машин). Машина, прибывшая в момент, когда все три места в очереди заняты, покидает АЗС (получает отказ). Найти характеристики СМО:

• вероятность отказа;

• относительную и абсолютную пропускную способности;

• среднее число занятых колонок;

• среднее число машин в очереди;

• среднее время ожидания и пребывания машины на АЗС.

Задача 2. Автозаправочная станция с четырьмя колонками обслуживает поток машин с интенсивностью λ = 0,8 (машин в минуту). Среднее время обслуживания одной машины 2,5 мин.

В данном районе нет другой АЗС, так что очередь машин перед АЗС может расти практически неограниченно. Найти характеристики СМО.

Задача 3. Определить оптимальное число постов зоны текущего ремонта, комплексного автотранспортного предприятия, если на каждом посту за смену можно отремонтировать два автомобиля, а потребность в ремонте - четыре автомобиля за смену. Известно, что затраты 1 часа простоя поста составляют 200 руб., 1 часа постоя техники – 450 руб., з/п рем. рабочих – 120 руб. в час. На каждом посту имеется по 1 слесарю.

Задача 4. Определить оптимальное число постов станции технического обслуживания если известно:

• вероятное изменение потока клиентов в течение года будет:

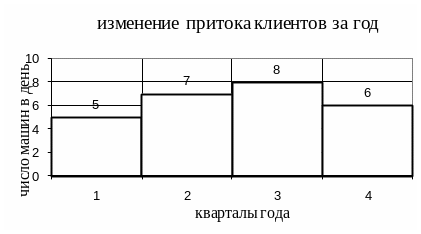
• среднее время обслуживания распределено по показательному закону и составляет: в летние месяцы – 4 часа на автомобиль, в зимние – 5,5 часов на автомобиль;

• известно, что средний оплата одного клиента составляет: летом – 550 руб. за услугу, зимой – 520 руб. за услугу;

• 1 час работы слесаря стоит 85 рублей;

• 1 час простоя поста составляет 130 руб.

• известно, что в среднем клиенты стоят в очереди не более 1,5 часов, потом уезжают.

5.5.Модель смо с ограниченным временем ожидания

Предположим, что имеется n – канальная СМО с ожиданием, в которой число мест в очереди не ограничено, но время пребывания заявки в очереди ограничено некоторым случайным сроком Т_оч. со средним значение _оч., таким образом, на каждую заявку, стоящую в очереди, действует как бы «поток уходов» с интенсивностью

.

Если этот поток пуассоновский, то процесс, протекающий в СМО, будет марковским. Найдем для него вероятности состояний. Будем снова нумеровать состояния системы по числу заявок, связанных с системой – как обслуживаемых, так и стоящих в очереди:

S₀ – все каналы свободны,

S₁ – занят один канал,

S₂ – заняты два канала,

. . . . . . . . . . . . . . . . . . . . .

S_n – заняты все n каналов,

S_n+1 – заняты все n каналов, одна заявка стоит в очереди,

. . . . . . . . .. . . . . . . .. . . . .

S_n+r – заняты все n каналов, r заявок стоит в очереди,

. . . . . . . . . . . . . . . . . . . . .

Формулы для расчета характеристик СМО будут следующие:

вероятность того, что все посты свободны:

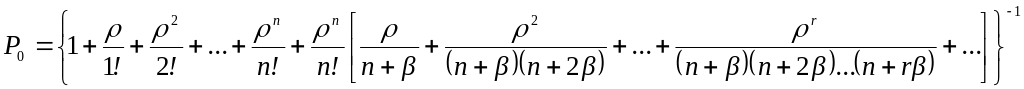, (5.0)

где β=ν/μ.

вероятность того, что занято k постов и r заявок стоит в очереди

. (5.0)

; (5.0)

абсолютная пропускная способность:

; (5.0)

относительная пропускная способность:

; (5.0)

среднее число заявок в очереди:

(5.0)

среднее число занятых каналов:

(5.0)

5.6.Модель замкнутой смо

До сих пор были рассмотрены такие модели, где заявки приходили откуда-то извне, и интенсивность потока заявок не зависела от состояния самой системы. В данном параграфе будут рассмотрены такие системы, в которых интенсивность потока поступающих заявок зависит от состояния самой системы. Такие системы массового обслуживания называются замкнутыми.

В качестве примера замкнутой СМО рассмотрим следующую систему. Рабочий-наладчик обслуживает п станков. Каждый станок может в любой момент выйти из строя и потребовать обслуживания со стороны наладчика. Интенсивность потока неисправностей каждого станка равна λ. Вышедший из строя станок останавливается. Если в этот момент рабочий свободен, он берется за наладку станка; на это он тратит среднее время

,

где μ – интенсивность потока обслуживания (наладок).

Если в момент выхода станка из строя рабочий занят, станок становится в очередь на обслуживание и ждет, пока рабочий не освободится.

Требуется найти вероятности состояний данной системы и ее характеристики:

• вероятность того, что рабочий не будет занят,

• вероятность наличия очереди,

• среднее число станков, ожидающих очереди на ремонт и т. д.

Перед нами — своеобразная система массового обслуживания, где источниками заявок являются станки, имеющиеся в ограниченном количестве и подающие или не подающие заявки в зависимости от своего состояния: при выходе станка из строя он перестает быть источником новых заявок. Следовательно, интенсивность общего потока заявок, с которым приходится иметь дело рабочему, зависит от того, сколько имеется неисправных станков, т. е. сколько заявок связано с процессом обслуживания (непосредственно обслуживается или стоит в очереди).

Характерным для замкнутой системы массового обслуживания является наличие ограниченного числа источников заявок.

В сущности, любая СМО имеет дело только с ограниченным числом источников заявок, но в ряде случаев число этих источников так велико, что можно пренебречь влиянием состояния самой СМО на поток заявок. Например, поток автомобилей на станцию СТО в крупном городе, в сущности ограничен, но это число так велико, что практически можно считать интенсивность потока заявок независимой от состояний самой СТО (сколько постов занято в данный момент). В замкнутой же системе массового обслуживания источники заявок, наряду с каналами обслуживания, рассматриваются как элементы СМО.

Рассмотрим сформулированную выше задачу о рабочем-наладчике в рамках общей схемы марковских процессов.

Система, включающая рабочего и п станков, имеет ряд состояний, которые мы будем нумеровать по числу неисправных станков (станков,

связанных с обслуживанием)

S₀ — все станки исправны (рабочий свободен);

S₁ — один станок неисправен, рабочий занят его наладкой;

S₂ — два станка неисправны, один налаживается, другой ожидает очереди;

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

S_n. — все п станков неисправны, один налаживается, п — 1 стоят

в очереди.

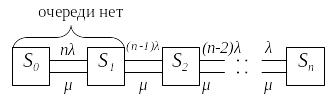
Рис. 5.20. Граф состояний замкнутой СМО с одним рабочим (обслуживающим механизмом)

Граф состояний приведен на рис. 5.5. Интенсивности потоков событий, переводящих систему из состояния в состояние, проставлены у стрелок. Из состояния S₀ в S₁, систему переводит поток неисправностей всех работающих станков; его интенсивность равна пλ. Из состояния S₁ в S₂ а систему переводит поток неисправностей уже не n, а п - 1 станков (работают всего п - 1) и т. д. Что касается интенсивностей потоков событий, переводящих систему по стрелкам справа налево, то они все одинаковы— работает все время один рабочий с интенсивностью обслуживания μ.

Пользуясь, как обычно, общим решением задачи о предельных вероятностях состояний для схемы гибели и размножения, вероятности состояний будут:

вероятность того, что рабочий свободен (все станки исправны):

; (5.0)

вероятности того, что какое-то число станков неисправно:

один станок неисправен): ; (5.0)

два станка неисправно (1 из них в ремонте, 1 в очереди):

; (5.0)

n станков неисправно (1 в ремонте, n-1 в очереди):

; (5.0)

вероятность того, что рабочий занят:

P_зан=1-P₀; (5.0)

абсолютная пропускная способность (среднее количество неисправностей, устраняемых рабочим в единицу времени):

A=(1-P₀)μ ; (5.0)

вероятность того, что рабочий свободен:

P_своб=1-P_зан=P₀; (5.0)

среднее число неисправных станков:

; (5.0)

среднее число станков, ожидающих наладки в очереди:

; (5.0)

потеря производительность группы станков:

L= · l, (5.0)

где l – производительность одного исправного станка.

Пример 1. Рабочий обслуживает группу из трех станков. Каждый станок останавливается в среднем 2 раза в час. Процесс наладки занимает у рабочего в среднем 10 минут. Определить характеристики замкнутой СМО: вероятность занятости рабочего, его абсолютную пропускную способность А; среднее количество неисправных станков; среднюю относительную потерю производительности группы станков за счет неисправностей.

Решение.

станков/час.

По формуле (5.41)

.

Вероятность занятости рабочего:

P_зан=1-Р₀=0,654.

Абсолютная пропускная способность (среднее количество неисправностей, которое он ликвидирует в час):

A=0,654 · 6=3,94 станка/час.

Среднее число неисправных станков:

станка.

Средняя относительная потеря производительности группы станков за счет неисправностей /n = 0,347, т .е. за счет неисправностей группа станков теряет около 35% производительности.

Рассмотрим теперь более общий пример замкнутой СМО: бригада из m рабочих обслуживает n станков (m<n). Перечислим состояния системы.

S₀ – все станки работают, рабочие не заняты;

S₁ – один станок остановился, один рабочий занят;

S₂ – два станка остановились, два рабочих заняты;

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

S_m – m станков остановились;

S_m+1 – m+1 станков остановились, m из них налаживаются, один ждет очереди;

S_n – все n станков остановились, m из них налаживаются, n-m ждут очереди.

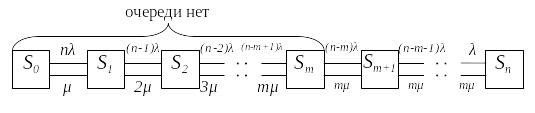
Рис. 5.21. Граф состояний замкнутой СМО с несколькими рабочими (обслуживающими аппаратами)

Соответственно формулы для нахождения характеристик эффективности для многоканальной системы будут:

вероятность того, что все рабочие свободны (все станки исправны):

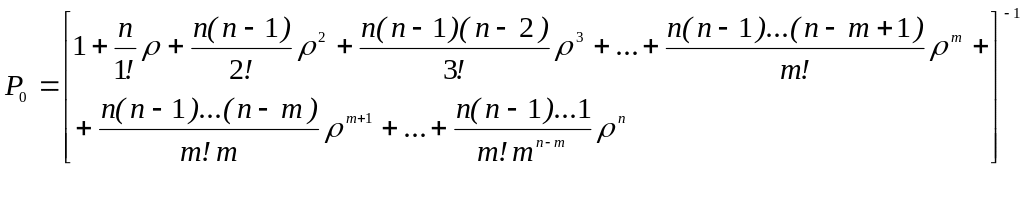(5.0)

вероятности того, что какое-то число станков неисправно:

один станок неисправен (занят один рабочий):

; (5.0)

два станка неисправно (занято двое рабочих):

; (5.0)

три станка неисправно (занято трое рабочих):

; (5.0)

m станков неисправно (заняты все m рабочих):

; (5.0)

m+1 станков неисправно (m в ремонте 1 в очереди):

; (5.0)

m+2 станка неисправно (m в ремонте 2 в очереди):

; (5.0)

все n станков неисправно (m в ремонте n-m в очереди):

; (5.0)

среднее число занятых рабочих:

M[m] (5.0)

абсолютная пропускная способность:

A= · μ; (5.0)

среднее число неисправных станков:

. (5.0)

Пример 2. Два рабочих обслуживают группу из шести станков. Остановки каждого (работающего) станка случаются, в среднем, через каждые полчаса. Процесс наладки занимает у рабочего в среднем 10 минут. Определить характеристики замкнутой СМО:

среднее число занятых рабочих;

абсолютную пропускную способность;

среднее количество неисправных штанов.

Решение.

станков/час;

P₁=6/1 · 1/3 · 0,153=0,306.

Определяем среднее число занятых рабочих:

.

Находим абсолютную пропускную способность:

A=1,235 · 6 = 7,41 станков/час.

Задача 1. Комплексное АТП имеет в своем распоряжении 10 автомобилей. Интенсивность поломок одного автомобиля в среднем 1 раз в 12 дней. На предприятии имеется зона ремонта с двумя постами. Среднее время ремонта одного автомобиля равно 5 часов. Определить характеристики функционирования системы если известно, что предприятие имеет 8-ми часовой рабочий день при 6-ти дневной рабочей неделе.

Задача 2. Торговая фирма имеет 5 постоянных клиентов. Каждый клиент, в среднем раз в неделю делает заказ на покупку товара. Время оформления заказа и доставка товара одному клиенту, в среднем составляет 2 дня. Вероятность того, что клиент закажет товара на сумму более 5000 у.е. равна 0,6. Определить минимальный доход, который может получить торговая фирма за месяц, если у нее в наличии имеется только два транспортных средства по доставке товара, причем каждое из них одновременно может доставлять товар только одному клиенту.

Задача 3. Автотранспортное предприятие имеет зону ТР с 3 постами. Среднесписочное количество автомобилей на предприятии – 8. Каждый автомобиль, в среднем в день, проезжает 170 км. Параметр потока отказов равен 0,9 отк./1000км. Среднее время ремонта одного автомобиля составляет 10 часов. Определить характеристики функционирования предприятия как СМО, коэффициент технической готовности парка.

6.Моделирование систем массового обслуживания с использованием метода статистических испытаний

Задачи, встречающиеся на практике, зачастую оказываются настолько сложными, что получить их характеристики с помощью аналитического метода невозможно (например, поток поступающих требований не является простейшим, время обслуживания не распределено по показательному закону, дисциплина обслуживания может быть достаточно сложной, кроме того, в системе могут существовать обратные связи и т.д.). В таких случаях целесообразно использовать метод моделирования СМО, справляющийся с перечисленными трудностями. Если процесс функционирования СМО случайный, то моделирование подобной системы состоит в построении реализаций случайного процесса.

Метод статистических испытаний позволяет исследовать зависимость эффективности системы обслуживания от параметров потока заявок и самой системы. Кроме того, этот метод позволяет оценить не только простейшие характеристики эффективности системы, но значения многих других важных показателей системы (дисперсию доли отказов, вероятность того, что значение доли отказов будет не ниже заданного и т.п.).

Сущность метода статистических испытаний применительно к анализу СМО состоит в следующем. С помощью специальных алгоритмов формируются реализации потока заявок с заданным законом распределения интервалов между заявками. Далее моделируется процесс функционирования обслуживающей системы. Все интересующие показатели работы системы фиксируются. Общий алгоритм модели многократно воспроизводит случайные реализации процесса функционирования системы при некоторых заранее заданных условиях. Накопленная в результате информация статистически обрабатывается.

Входящий поток требований однозначно задается последовательностью моментов времени поступления заявок в систему T₁, T₂, ... Однако для моделирования удобнее рассматривать случайные величины τ_k, определяющие длину интервалов между моментами поступления заявок. Тогда для задания входящего потока достаточно получить последовательность случайных величин τ_k с заданным законом распределения.

Датчик нормально распределенного случайного числа.

Плотность нормального распределения имеет вид:

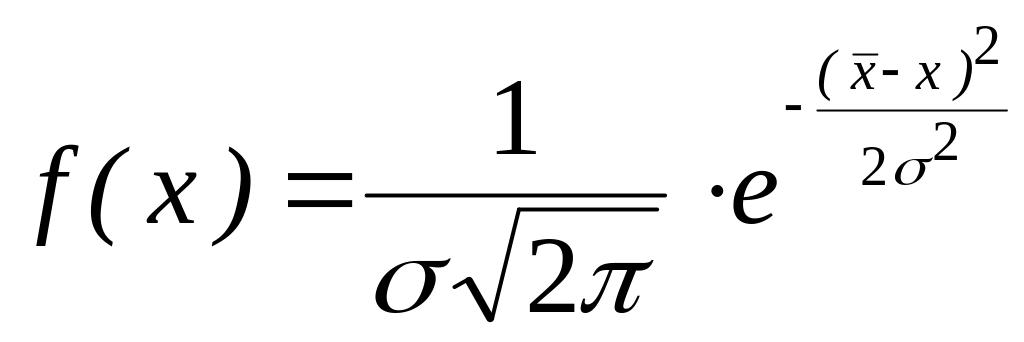
Сначала необходимо сложить шесть равномерно-распределенных случайных чисел от 0 до 1.

V=R₁+ R₂+ R₃+ R₄+ R₅+ R₆,

где R₁…R₆ – шесть независимых экземпляров случайного числа от 0 до 1.

По теореме сложения математических ожиданий находим математическое ожидание величины V:

M_v = 6 · 0,5 = 3.

Дисперсию случайной величины V можно найти по теореме сложения дисперсий:

D_v=D_r1+ D_r2+ D_r3+ D_r4+ D_r5+ D_r6;

где D_r1… D_r6 – дисперсии величин R₁…R₆.

Таким образом, дисперсия величины V будет равна:

D_v=6 · 1/12=1/2,

а среднеквадратическое отклонение

Пронормируем величину V, т .е. перейдем от нее к величине

;

Потом, подставляя значения, получим формулу для розыгрыша нормально распределенной случайной величины X, с математическим ожиданием M_x.

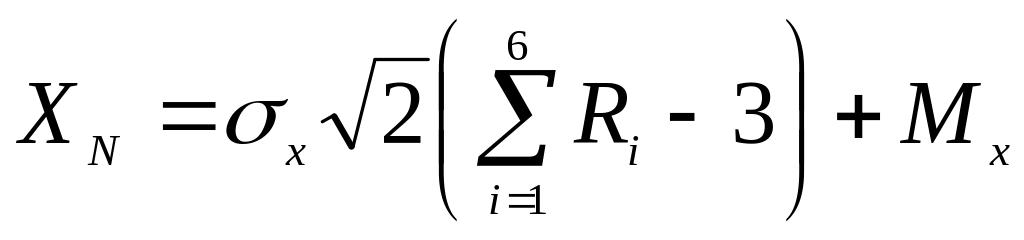. (6.0)

Датчик случайного числа, подчиненного распределению Вейбулла.

Плотность распределения Вейбулла имеет вид:

.

Если R – равномерно распределенная случайная величина на интервале (0…1), то

, (6.0)

где a – параметр масштаба, косвенно связанный со средним значением;

b – параметр формы, косвенно связанный со значением коэффициента вариации.

Датчик случайного числа, подчиненного логарифмически нормальному распределению.

Плотность логарифмически нормального распределения имеет вид:

.

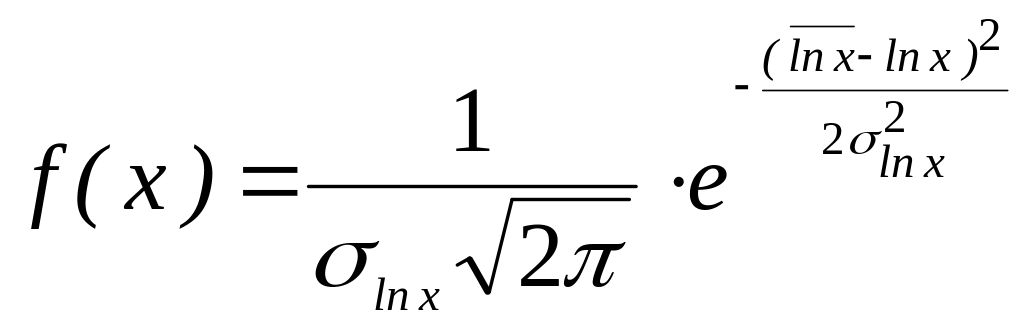Случайная величина, подчиненная логарифмически нормальному распределению имеет вид:

(6.0)

где η – нормально распределенная случайная величина с параметрами M_x=0, σ = 1;

– математическое ожидание разыгранной случайной величины.

Датчик случайного числа, подчиненного гамма распределению.

Плотность гамма распределения имеет вид:

.

Случайная величина, подчиненная гамма распределению имеет вид:

. (6.0)

Датчик случайного числа, подчиненного экспоненциальному распределению.

Плотность экспоненциального распределения имеет вид:

.

Случайная величина, подчиненная экспоненциальному распределению имеет вид:

. (6.0)

Те же приемы используются и для формирования случайных значений времени обслуживания.

Рассмотрим одну из простых систем массового обслуживания, которая состоит из 3 одинаковых каналов; входящий поток - простейший с параметром l; время обслуживания в канале одного требования постоянно и равно t_об. Система без ожидания, т.е. требование, заставшее все каналы занятыми, покидает систему. Дисциплина обслуживания такова: если в момент поступления k-гo требования, первый канал свободен, то он приступает к обслуживанию требования; если этот канал занят, то требование обслуживает второй канал и т.д. Требуется определить, сколько требований в среднем обслужит система за время Т и сколько в среднем она даст отказов?

За начальный момент расчета выбирают момент поступления первого требования. Введем следующие обозначения:

T_k – момент поступления k-го требования;

τ_k – промежуток времени между поступлением в систему k-го и (k+1)-го требования;

t_i – момент окончания обслуживания требования i-м каналом.

Предположим, что в момент T₁ все каналы свободны. Первое требование поступает на 1-й канал. Таким образом, в течение времени t_об этот канал занят. Поэтому полагают t₁=T₁+ t_об, добавляют единицу к счетчику обслуженных требований и переходят к рассмотрению второго требования.

Предположим, что k требований уже рассмотрено. Определим момент поступления (k+1)-го требования. Для этого найдем очередное значение х_k, равномерно распределенной случайной величины, и вычислим очередное значение по формуле 3.1, а затем момент поступления (k+1)-го требования.

T_k+1=t_k+τ_k.

Чтобы узнать свободен ли в этот момент первый канал необходимо проверить условие t₁ T_k+1. Если это условие выполнено, то к моменту T_k+1 первый канал освободился и может обслуживать требование. В этом случае заменяем значение t₁ на T_k+1+t_об и добавляем единицу к счетчику обслуженных требований и переходим к следующему требованию.

Если t₁ T_k+1, то первый канал в момент T_k+1 занят. В этом случае проверяем, свободен ли второй канал. Если условие t₂ T_k+1 выполнено, заменяем t₂ на T_k+1+t_об и добавляем единицу к счетчику обслуженных требований и переходим к следующему требованию.

Если t₂ T_k+1, то проверяем условие t₃ T_k+1. Если все каналы оказались заняты, то в этом случае прибавляем единицу в счетчик отказов и переходим к рассмотрению следующего требования.

Результаты моделирования можно оформить в виде следующей таблицы:

Каждый раз, вычислив T_k+1, надо проверить еще условие окончания реализации: T_k+1+>T. Если это условие выполнено, то одна реализация случайного процесса функционирования системы воспроизведена и опыт заканчивается. В счетчике обслуженных требований и в счетчике отказов находятся числа n_обс и.n_отк

Получив N реализаций случайного процесса, т.е., повторив такой опыт N раз, определяем оценки математических ожиданий числа обслуженных требований M(n_обс) и числа требований, получивших отказ M(n_отк).

7.Задания для контрольных работ

Задание 1. В комплексном автотранспортном предприятии имеется парк техники из 250 единиц, из них 35 единиц – легковые, остальные – грузовые. Доля заявок на устранение отказа в зону ТР составляет в среднем 7% от общей численности. Заявки поступают каждый день. Среднее время ремонта для грузовых автомобилей составляет 10 часов, для легковых – 7 часов. Легковые и грузовые автомобили обслуживаются на разных специализированных постах, а универсальный пост используется всеми. Известно что, 35% общих заявок используют универсальный пост.

Смоделировать работу зоны ТР за полгода. Определить основные показатели системы. Определить такое число специализированных и универсальных постов, при котором в очереди бы стояло не более 2 единиц техники каждого вида. Сравнить смоделированные показатели работы зоны с рассчитанными по формулам СМО.

Задание 2. В крупном автотранспортном предприятии кроме зоны ТР имеется пост диагностирования. Известно, что средняя интенсивность заявок на диагностику равна 18 заявок в день. Среднее время проведения диагностирования составляет 35 минут. 35% заявок после диагностирования направляются в зону ТР для устранения выявленных неполадок. Определить оптимальное число постов зоны ТР с учетом того, чтобы в очереди стояло не более 3 машин. Каждая заявка в среднем ремонтируется 3,5 часа. Рабочий день длится 8 часов.

Задание 3. На станцию технического обслуживания поступает поток автомобилей с различными видами и интенсивностью отказов:

• подвеска – 5 отказов в день, время устранения – 6,5 часов;

• система питания – 4 отказа в день, время устранения – 2,5 часа;

• электрооборудование – 4 отказа в день, время устранения – 2 часа;

• прочие 3 – отказов в день, время устранения – 2 часа.

Коме того у 10% прибывающих машин в процессе ремонта обнаруживают еще различные виды отказов: вероятность обнаружения еще одного отказа 0,85, еще двух 0,15.

Устранения первых двух видов отказов выполняется на специализированных постах. Отказы Электрооборудования и прочие – на универсальных. Общая площадка для ожидания может вместить не более 7 машин.

Кроме того, если специализированный пост простаивает, то слесарь с этого поста помогает устранять другие виды отказов (выбор происходит случайным образом), в результате чего производительность труда увеличивается на 25%.

Необходимо смоделировать работу СТО за месяц с учетом 10 часового рабочего дня, определив при этом основные характеристики по каждому посту в отдельности.

Задание 4. На обрабатывающий участок цеха поступают детали в среднем через 50 мин. Первичная обработка деталей производится на одном из двух станков. Первый станок обрабатывает деталь в среднем 40 мин и имеет до 4% брака, второй соответственно 60 мин и 8% брака. Все бракованные детали возвращаются на повторную обработку на второй станок. Детали, попавшие в разряд бракованных дважды, считаются отходами. Вторичную обработку проводят также два станка в среднем 100 мин. каждый. Причем первый станок обрабатывает имеющиеся в накопителе после первичной обработки детали, а второй станок подключается при образовании в накопителе задела больше трех деталей. Все интервалы времени распределены по экспоненциальному закону.

Смоделировать обработку на участке 500 деталей. Определить нагрузку второго станка на вторичной обработке и" вероятность появления отходов. Определить возможность снижения задела в накопителе и повышения загрузки второго станка на вторичной обработке.

Задание 5. На регулировочный участок цеха через случайные интервалы времени поступают по два агрегата в среднем через каждые 30 мин. Первичная регулировка осуществляется для двух агрегатов одновременно и занимает около 30 мин. Если в момент прихода агрегатов предыдущая партия не была обработана, поступившие агрегаты на регулировку не принимаются. Агрегаты после первичной регулировки, получившие отказ, поступают в промежуточный накопитель. Из накопителя агрегаты, прошедшие первичную регулировку, поступают попарно на вторичную регулировку, которая выполняется в среднем за 30 мин, а не прошедшие первичную регулировку поступают на полную, которая занимает 100 мин для одного агрегата. Все величины, заданные средними значениями, распределены экспоненциально.

Смоделировать работу участка в течение 100 ч. Определить вероятность отказа в первичной регулировке и загрузку накопителя агрегатами, нуждающимися в полной регулировке. Определить параметры и ввести в систему накопитель, обеспечивающий безотказное обслуживание поступающих агрегатов.

 Задание 6. На сборочный участок цеха предприятия через интервалы времени, распределенные экспоненциально со средним значением 10 мин, поступают партии, каждая из которых состоит из трех деталей. Половина всех поступающих деталей перед сборкой должна пройти предварительную обработку в течение 7 мин. На сборку подаются обработанная и необработанная детали. Процесс сборки занимает всего 6 мин. Затем изделие поступает на регулировку, продолжающуюся в среднем 8 мин (время выполнения ее распределено экспоненциально). В результате сборки возможно появление 4% бракованных изделий, которые не поступают на регулировку, а направляются снова на предварительную обработку.

Смоделировать работу участка в течение 24 ч. Определить возможные места появления очередей и их вероятностно-временные характеристики. Выявить причины их возникновения, предложить меры по их устранению и смоделировать скорректированную систему.

Задание 7. На участке термической обработки выполняются цементация и закаливание шестерен, поступающих через 10 ± 5 мин. Цементация занимает 10 ± 7 мин, а закаливание — 10 ± 5 мин. Качество определяется суммарным временем обработки. Шестерни с временем обработки больше 25 мин покидают участок, с временем обработки от 20 до 25 мин передаются на. повторную закалку и при времени обработки меньше 20 мин. должны пройти повторную полную обработку. Детали с суммарным временем обработки меньше 20 мин считаются вторым сортом.

Смоделировать процесс обработки на участке 400 шестерен. Определить функцию распределения времени обработки и вероятности повторения полной и частичной обработки. При выходе продукции без повторной обработки менее 90% обеспечить на участке мероприятия, дающие гарантированный выход продукции первого сорта 90%.

Задание 8. На комплектовочный конвейер сборочного цеха каждые 5 ± 1 мин поступают 5 изделий первого типа и каждые 20 ± 7 мин поступают 20 изделий второго типа. Конвейер состоит из секций, вмещающих по 10 изделий каждого типа. Комплектация начинается только при наличии деталей обоих типов в требуемом количестве и длится 10 мин. При нехватке деталей секция конвейера остается пустой.

Смоделировать работу конвейера сборочного цеха в течение 8 ч. Определить вероятность пропуска секции, средние и максимальные очереди по каждому типу изделий. Определить экономическую целесообразность перехода на секции по 20 изделий с временем комплектации 20 мин.

Задание 9. Транспортный цех объединения обслуживает три филиала А, В и С. Грузовики перевозят изделия из А в B и из В а С, возвращаясь затем в А без груза. Погрузка в K занимает 20 мин, переезд из А в B длится 30 мин, разгрузка и погрузка в B— 40 мин, переезд в С— 30 мин разгрузка в С— 20 мин и переезд в А— 20 мин. Если к моменту погрузки а A и В отсутствуют изделия, грузовики уходят дальше по маршруту. Изделия в А выпускаются партиями по 1000 шт. через 20±3 мин, в B — такими же партиями через 20±5 мин. На линии работает 8 грузовиков, каждый перевозит 1000 изделий. В начальный момент все грузовики находятся в А.

Смоделировать работу транспортного цеха объединения в течение 1000 ч. Определить частоту пустых перегонов грузовиков между А и В, В и С и сравнить с характеристиками, полученными при равномерном начальном распределении грузовиков между филиалами и операциями. Обосновать оптимальное число грузовиков на линии.

Задание 10. Специализированная вычислительная система состоит из трех процессоров и общей оперативной памяти Задания, поступающие на обработку через интервалы времени 5±2 мин, занимают объем оперативной памяти размером в страницу. После трансляции первым процессором в течение 5±1 мин их объем увеличивается до двух страниц, и они поступают в оперативную память. Затем после редактирования во втором процессоре, которое занимает 2,5±0,5 мин на страницу, объем возрастает до трех страниц. Отредактированные задания через оперативную память поступают в третий процессор на решение, требующее 1,5±0,4 мин на страницу, и покидают систему, минуя оперативную память.

Смоделировать работу вычислительной системы в течение 50 ч. Определить характеристики занятия оперативной памяти по всем трем видам заданий. Определить структуру системы при увеличении в. 2 раза частоты поступлений заявок.

Задание 11. На вычислительном центре в обработку принимаются три класса заданий А,В и С, Исходя из наличия оперативной памяти ЭВМ задания классов А и В могут решаться одновременно, а задания класса С монополизируют ЭВМ. Задания класса А поступают через 20 ±5 мин, класса 6 — через 20 ± 10 мин и класса С — через 30 ± 10 мин и требуют для выполнения- класс А —20±5 мин, класс В —21±3 мин и класс С —28±5 мин Задачи класса С загружаются в ЭВМ, если она полностью свободна. Задачи классов А и В ^:могут дозагружаться к решающейся задаче.

Смоделировать работу ЭВМ за 80 ч. Определить ее загрузку. В случае необходимости дать рекомендации по подключению других ЭВМ.

Задание 12. В студенческом научном центре расположены два высокопроизводительных компьютера и один компьютер прошлых поколений, позволяющий производить только печать на принтере. Студенты приходят с интервалом в 8±2 мин, и треть из них хочет использовать принтер и высокопроизводительный компьютер, а остальные только компьютер. Допустимая очередь в зале составляет четыре человека, включая печатающего на принтере. Печать на принтере занимает 8 ± 1 мин, а работа на компьютере — 20 мин. Кроме того, 20% работавших на компьютере возвращается для повторного использования принтера и высокопроизводительного компьютера.

Смоделировать работу центра в течение 60 ч. Определить загрузку принтера и первых двух компьютеров, вероятности отказа в обслуживании вследствие переполнения очереди. Определить соотношение в очереди желающих работать на принтере и на высокопроизводительных компьютерах. Рассмотреть возможные меры по улучшению обслуживания студентов.

Смоделировать работу мини-ЭВМ в течение 4 ч. Определить загрузку процессора, вероятности простоя терминалов и частоту одновременного выполнения трансляции с трех терминалов. Определить оптимальное число терминалов.

Задание 13. Система автоматизации проектирования состоит из ЭВМ и трех терминалов. Каждый проектировщик формирует задание на расчет в интерактивном режиме. Набор строки задания занимает 10±5 с. Получение ответа на строку требует 3 с работы ЭВМ и 5с работы терминала, После набора десяти строк задание считается сформированным и поступает на решение, при этом в течение 10±3 с ЭВМ прекращает выработку ответов на вводимые строки. Вывод результата требует 8 с работы терминала. Анализ результата занимает у проектировщика 30 с, после чего цикл повторяется.

Смоделировать работу системы в течение б ч. Определить вероятность простоя проектировщика из-за занятости ЭВМ и коэффициент загрузки ЭВМ. Определить оптимальное количество терминалов.

Задание 14. Клиенты прибывают на СТО в случайные моменты времени. Интервалы между приходами имеют нормальное распределение с математическим ожиданием 30 мин. и дисперсией 7 мин. Часть клиентов с вероятностью 0,7 едут на ремонт, остальные – на диагностирование. Очередь в кассу общая. Время обслуживания имеет равномерное распределение:

- в ремонтном отделе на интервале от 80 до 150 мин.;

- на посту диагностирования на интервале от 30 до 50 мин.;

- в кассе на оформление заявки на интервале от 2 до 3 мин.

Определить число постов диагностирования и текущего ремонта, чтобы средняя длина очереди не превышала 2-х человек. Рассчитать при этом основные показатели качества системы (в т.ч. частотные).

Задание 15. Детали, необходимые для работы цеха, находятся на цеховом и центральном складах. На цеховом складе хранится 20 комплектов деталей, потребность в которых возникает через 60±10 мин и составляет один комплект. В случае снижения запасов до трех комплектов формируется в течение 60 мин заявка на пополнение запасов цехового склада до полного объема в 20 комплектов, которая посылается на центральный склад, где в течение 60±20 мин происходит комплектование и за 60±5 мин. осуществляется доставка деталей в цех.

Смоделировать работу цеха в течение 400 ч. Определить вероятность простоя цеха из-за отсутствия деталей и среднюю загрузку цехового склада. Определить момент пополнения запаса цехового склада, при котором вероятность простоя цеха будет равна 0.

 Задание 16. В вычислительную машину, работающую в системе управления технологическим процессом, через каждые 3±1 с поступает информация от датчиков и измерительных устройств. До обработки на ЭВМ информационные сообщения накапливаются в буферной памяти. Продолжительность обработки сообщений на ЭВМ — 6±2 с. Динамика технологического процесса такова, что имеет смысл обрабатывать сообщения, ожидавшие в буферной памяти не более 12 с. Остальные сообщения считаются потерянными.

Смоделировать процесс поступления в ЭВМ 200 сообщений. Подсчитать число потерянных сообщений и определить коэффициент загрузки ЭВМ. Определить количество ЭВМ для оптимального функционирования технологического процесса.

Задание 17. Самолеты прибывают для посадки в район крупного аэропорта каждые 10±5 мин. Если взлетно-посадочная полоса свободна, прибывший самолет получает разрешение на посадку. Если полоса занята, самолет выполняет полет по кругу и возвращается к аэропорту через каждый 4 мин. Если после пятого круга самолет не получает разрешения на посадку, он отправляется на запасной аэродром. в аэропорту через каждые 10±2 мин к взлетно-посадочной полосе выруливают готовые к взлету машины и получают разрешение на  взлет, если полоса свободна. Для взлета и посадки самолеты занимают полосу ровно на 2 мин. Если при свободной полосе одновременно один самолет прибывает для посадки, а другой — для взлета, полоса предоставляется взлетающей машине.

Смоделировать работу аэропорта в течение суток. Подсчитать количество самолетов, которые взлетели, сели и были направлены на запасной аэродром. Определить коэффициент загрузки взлетно-посадочной полосы. Сколько взлетно-посадочных полос необходимо, чтобы не задействовать запасной аэродром.

Задание 18. Диспетчер управляет внутризаводским транспортом и имеет в своем распоряжении два грузовика. Заявки на перевозки поступают к диспетчеру каждые 5 + 4 мин. С вероятностью 0,5 диспетчер запрашивает по радио один из грузовиков и передает ему заявку, если тот свободен. В противной случае он запрашивает другой грузовик и таким образом продолжает сеансы связи, пока один из грузовиков не освободится. Каждый сеанс связи длится ровно 1 мин. Диспетчер допускает накопление у себя до пяти заявок, после чего вновь прибывшие заявки получают отказ. Грузовики выполняют заявки на перевозку за 12 ± 8 мин.

Смоделировать работу внутризаводского транспорта в течение 10 час. Подсчитать число обслуженных и отклоненных заявок. Определить коэффициенты загрузки грузовиков. Дать рекомендации по количеству грузовиков, чтобы заявки не получали отказ.

Задание 19. Пять операторов работают в справочной телефонной сети города, сообщая номера телефонов по запросам абонентов, которые обращаются по одному номеру 09. Автоматический коммутатор переключает абонента на того оператора, в очереди которого ожидает наименьшее количество абонентов, причем наибольшая допустимая длина очереди перед оператором — два абонента. Если все очереди имеют максимальную длину, вновь поступивший вызов получает отказ; 0бслуживание абонентов операторами длится 30±20 с. Вызовы поступают в справочную через каждые 5±3 с.

Смоделировать обслуживание 200 вызовов. Подсчитать количество отказов. Определить коэффициенты загрузки операторов справочной. Определить необходимое число операторов, чтобы заявки не получали отказ.

Литература

1. Советский энциклопедический словарь. – М.: Советская энциклопедия, 1985. – 1600 с.

2. Хубка В. Теория технических систем: Пер. с нем. – М.: Мир, 1987. – 208 с.

3. Лифшиц В.Н. Системный анализ экономических процессов на транспорте. – М.: Транспорт, 1986. – 240 с.

4. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1964. - 576 с.

5. Вентцель Е.С. Исследование операций. - М.: Советское радио, 1972. - 552 с.

6. Гнеденко Б.В., Беляев В.К., Соколов А.Д. Математические методы в теории надежности. – М.: Наука, 1965. – 524 с.

7. Советов Б.Я., Яковлев С.А. Моделирование систем: Лабораторный практикум. – М.: Высшая школа, 1989. – 80 с.

8. Техническая эксплуатация автомобилей / Е.С. Кузнецов, А.П. Болдин, В.М. Власов и др. – М.: Наука, 2001. – 535 с.

9. Болдин А.П., Максимов В.А. Основы научных исследований и УНИРС/Учебное пособие. 2-е издание, перераб. и дополн.­М., 2002. -276 с.

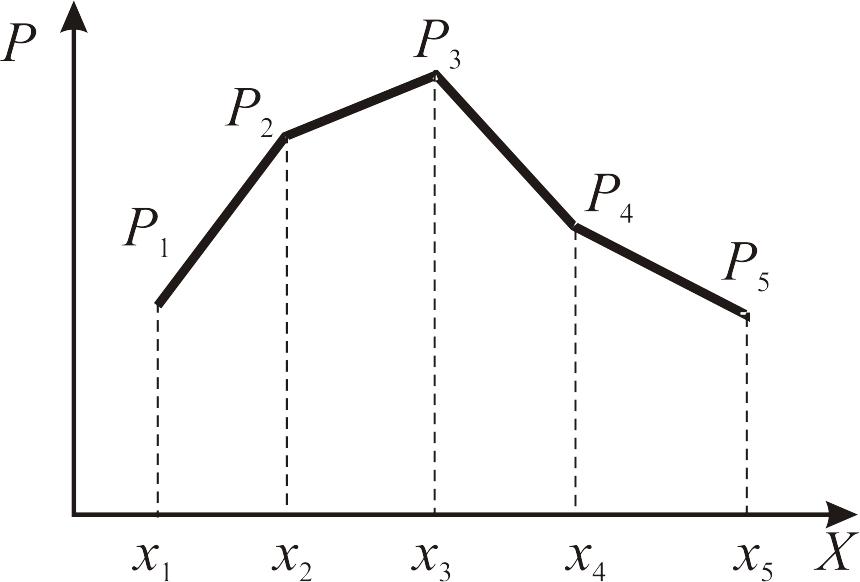
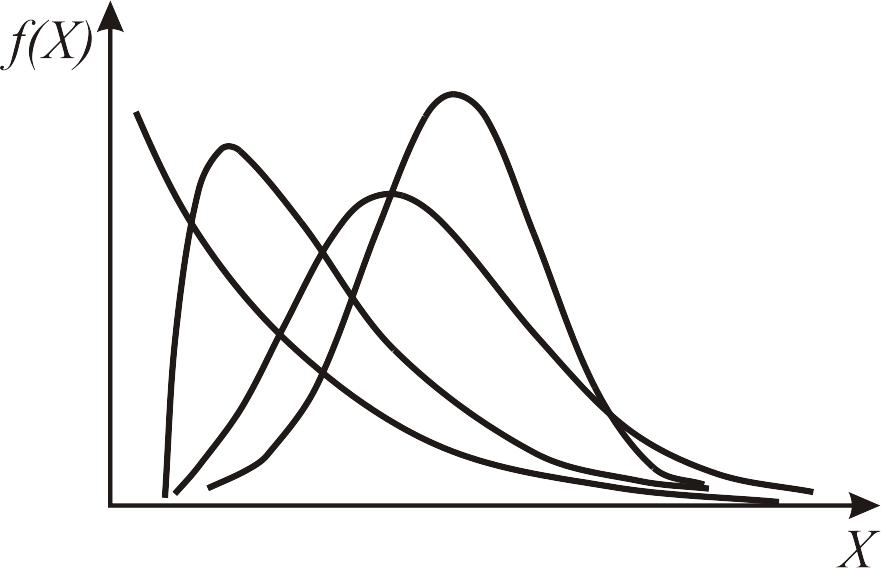
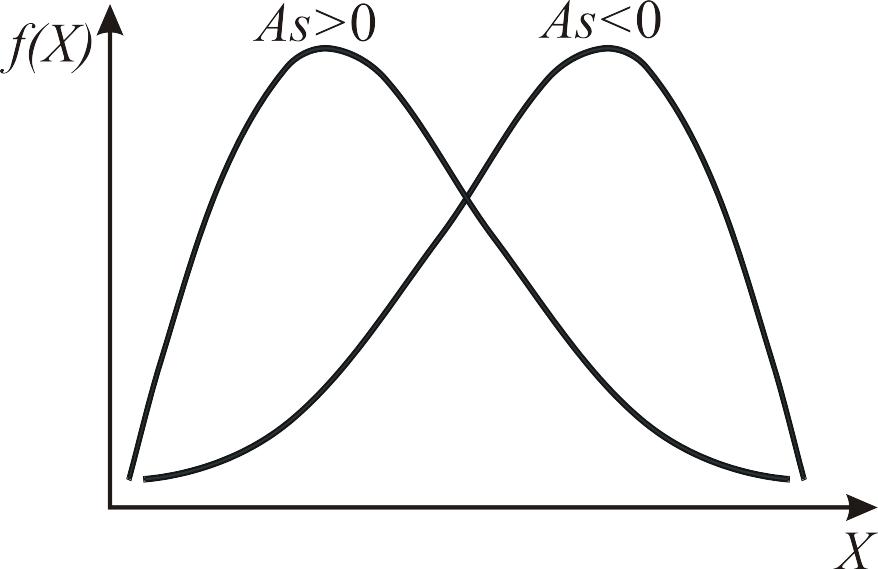
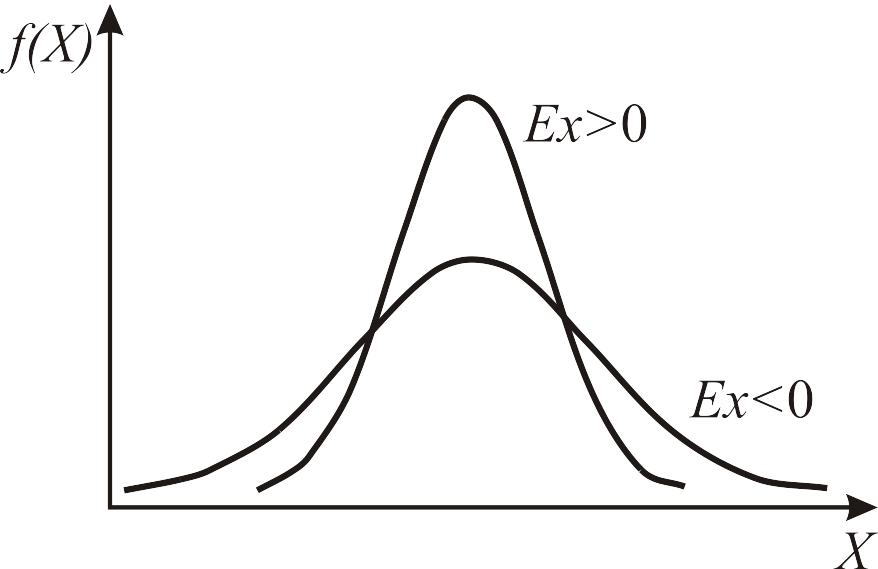
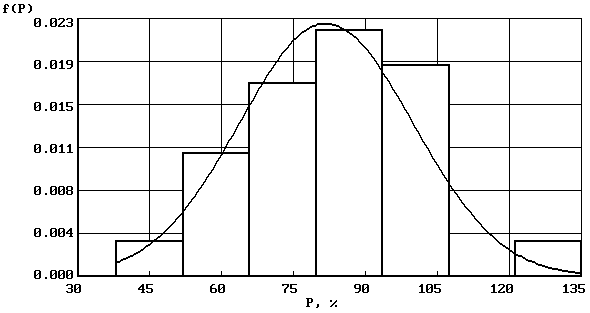
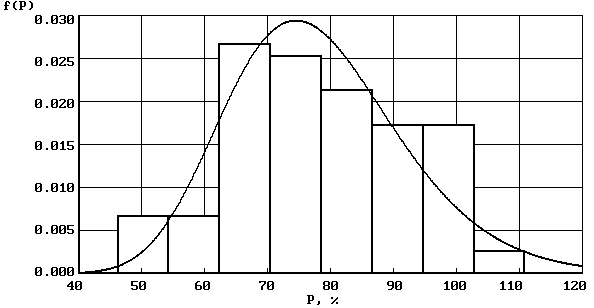
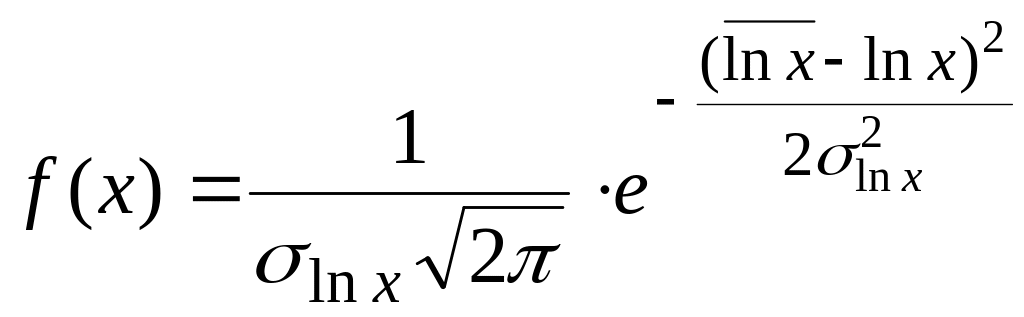
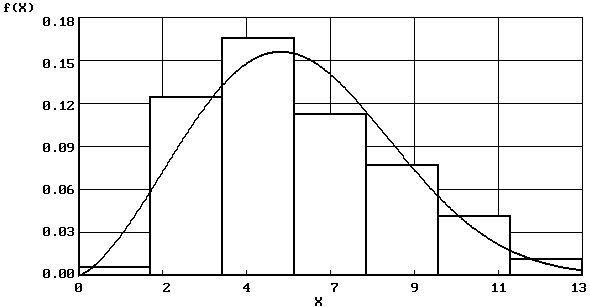
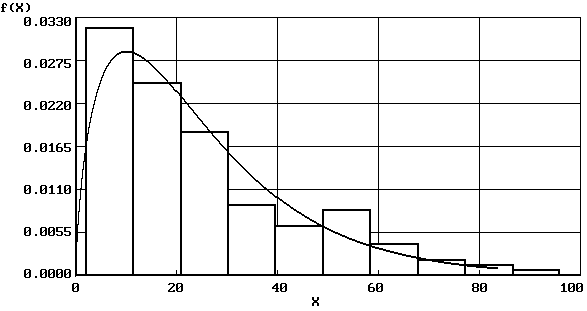
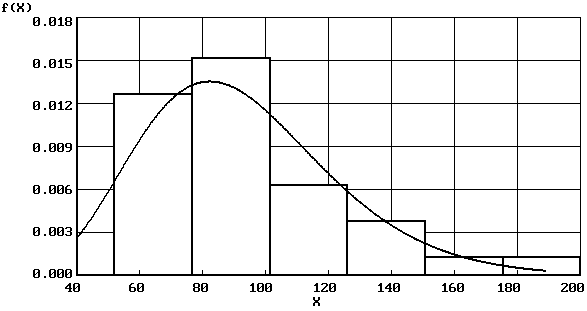
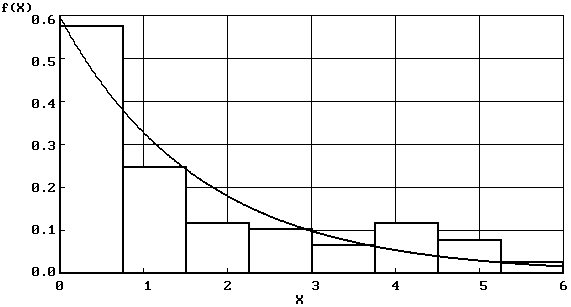
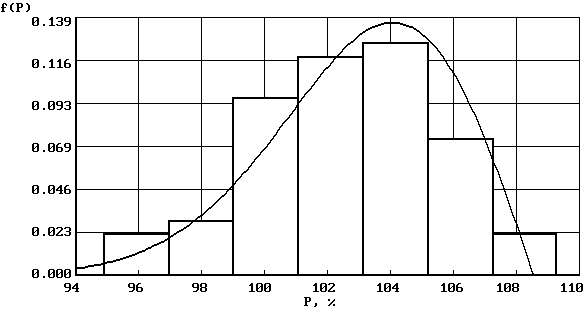
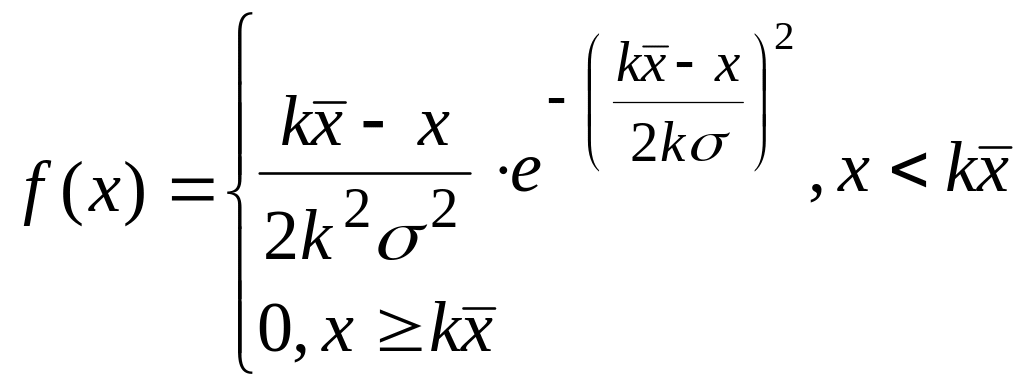83