Прямозубая передача
Расчетное допускаемое контактное напряжение принимают меньшее из значений:
[σH] = 0,45([σH1]+[σH2]) = 0,45(452+386)=377 МПа
[σH] = 1,23[σH2] = 1,23*386=475 МПа
Принимаем [σH] = 377 МПа.
Допускаемое напряжение изгиба при расчете на выносливость
[σF] = σ˚Flim/[SF],
где σ˚Flim =1,8 HB – предел выносливости зубьев при базовом числе циклов нагружения (МПа),
[SF] = 1,8÷2,0 – коэффициент безопасности.
Для шестерни [σF1] = 1,8 * 240 / 2 = 216 МПа.
Для колеса [σF2] = 1,8 * 200 / 2 = 180 МПа.
3.2 Межосевое расстояние зубчатой передачи из условия контактной выносливости активных поверхностей зубьев вычисляется по формуле:
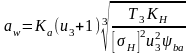
49 –
коэффициент межосевого расстояния для
косозубой передачи
uзп = u = 3 – принятое передаточное число
Т3 = 126,6 Н*м – вращающий момент на валу колеса
КH = 1,25 – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями и по ширине венца колеса
[σH] = 377 МПа – найденное допускаемое напряжение
Ψba = b/aw – коэффициент ширины колеса (выбирается из ряда 0,315; 0,4; 0,5)
Принимаем Ψba = 0,315, тогда:
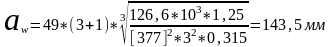
По ГОСТ 2185-66 принимаем aw = 160 мм
3.3 Нормальный модуль зацепления:
mn = (0,01÷0,02)*aw = (0,01÷0,02)*160 = 1,6÷3,2 мм
По ГОСТ 9563-60 принимаем mn = 2 мм
3.4 Суммарное число зубьев колес:
z = z1 + z2 = 2aw*cosβ/mn,
где β = 0˚
z = 2*160*1/2 = 160 – число зубьев
3.5 Число зубьев шестерни и колеса
z1 = z/(u2+1) = 160/(3+1) = 40
z2 = z – z1 = 160 – 40 = 120
3.6 Уточняем передаточное число редуктора u2 = z2/z1 = 120/40 = 3
3.7 Основные размеры шестерни и колеса.
Диаметры делительные
d1 = mn*z1/cosβ = 2*40/1 = 80 мм
d2 = mn*z2/cosβ = 2*120/1 = 240 мм
Проверка:
aw = (d1+d2)/2 = (80 + 240)/2 = 160 мм
Диаметры вершин зубьев
da1 = d1 + 2mn = 80 + 2*2 = 84 мм
da2 = d2 + 2mn = 240 + 2*2 = 244 мм
Диаметры впадин зубьев:
df1 = d1 – 2,5mn = 80 – 2,5*2 = 75 мм
df2 = d2 – 2,5mn = 240 – 2,5*2 = 235 мм
Ширина колеса:
b2 = Ψba*aw = 0,315*160 = 50 мм
Ширина шестерни:
b1 = b2 + 5 = 55 мм
3.8 Силы действующие в зацеплении
Окружная:
Ft2
= 2T3/d2
= 2*126,6*10
/240
= 1055 H
Радиальная силa: Fr2 = Ft2*tgα/cosβ = 1055*tg20˚/cosβ = 1055*0,364/1 = 384 H
Осевая сила: Fa2 = Ft2*tgβ = 1055*0 = 0 H
3.9 Проверка условия прочности на выносливость по контактным напряжениям
291 МПа < [σH] = 377 МПа
3.10 Проверка зубьев на выносливость по напряжениям изгиба
zv2 = z2/cos3β = 120/13 = 120, принимаем YF = 3,61
YF – коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа зубьев zv.
σF = 1055*2*3,61/(50*2) = 76,2МПа ≤ [σF2] = 180 МПа
Условие прочности на выносливость по напряжениям изгиба выполняется с запасом. Это подтверждает, что для зубчатых колес, работающих в масле (редуктор), определяющей является выносливость по контактным напряжениям активной поверхности зубьев.
Величина |
Обозначение |
Единица величины |
Значения косозубой (б/х) |
Значения прямозубой (т/х) |
|||
Межосевое расстояние |
aw |
мм |
90 |
160 |
|||
Модуль нормальный |
mn |
мм |
1,75 |
2 |
|||
Угол наклона зубьев |
β |
˚ |
13˚53ʹ |
0˚ |
|||
Передаточное число |
U1, U2 |
- |
3 |
3 |
|||
|
|
|
Шестерня |
Колесо |
Шестерня |
Колесо |
|
Число зубьев |
z1, z2 |
- |
25 |
75 |
40 |
120 |
|
Диаметр делительный |
d1, d2 |
мм |
45 |
135 |
80 |
240 |
|
Диаметр вершин зубьев |
da1, da2 |
мм |
49 |
139 |
84 |
244 |
|
Диаметр впадин зубьев |
df1, df2 |
мм |
40 |
130 |
75 |
235 |
|
Ширина колес |
b1, b2 |
мм |
41 |
36 |
55 |
50 |
|
Силы в зацеплении |
|
|
|||||
Окружная |
Ft |
H |
644,4 |
1055 |
|||
Радиальная |
Fr |
H |
241,3 |
384 |
|||
Осевая |
Fa |
H |
155,2 |
0 |
|||