ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Федеральное государственное образовательное бюджетное учреждение высшего

профессионального образования

«Санкт-Петербургский государственный университет телекоммуникаций

им. проф. М.А. Бонч-Бруевича»

_____________________________________________________________________________

Методические указания к лабораторным работам:

Исследование сжатия периодических сигналов в среде Matlab

Изучение моделей вокодеров и подготовка данных для разработки модели исследования

Исследование удаления формант из речевых сигналов

Разработчик

проф. Рыжков А.Е.

Санкт-Петербург

2012г

Оглавление

1. Введение 3

2. Теоретические положения 4

3. Постановка задачи. Сжатие синусоидального сигнала с помощью ДИКМ……………………………………………………………5

4. Сжатие речевого сигнала…………………………………… 20

5. Итоговая реализация…………………………………..............30

6. Рекомендуемая литература ………………………….………..31

7. Требования к отчету……………………………………..….…32

8. Приложение 1…………………………………………………..33

Введение

В современных цифровых системах с целью уменьшения скорости передачи речи по каналам связи применяются различные методы сжатия. В таких системах речевой сигнал, преобразованный в цифровой вид, перед передачей кодируют при помощи специального алгоритма сжатия, а при воспроизведении на приеме - декодируют.

Как известно, речевой сигнал в информационно - коммуникативном плане обладает определенной избыточностью, не влияющей на смысловое содержание речевой посылки. При этом сжатие речи возможно за счет частичного удаления этой избыточности, что может не уменьшать разборчивости и качества слухового восприятия речи, но, вместе с тем, лишить ее особых признаков, необходимых для экспертной идентификации речи. Поэтому при производстве экспертизы важно установить как сам факт сжатия, так и его влияние на речевой сигнал.

В настоящее время применяют множество алгоритмов сжатия речи. Все они могут быть реализованы как аппаратными, так и программными методами. Одной из групп таких алгоритмов являются усовершенствованные виды импульсно-кодовой модуляции (ИКМ, Pulse-Code Modulation PCM).

Параметры ИКМ при оцифровке речевых сигналов описаны в рекомендациях МККТТ (Международный консультативный комитет по телефонии и телеграфии, CCITT) и, как правило, имеют следующие значения: - частота дискретизации 8000 Гц; - число двоичных разрядов на отсчет 8;

- скорость передачи 64000 бит/c.

При этом может быть оцифрован и восстановлен аналоговый сигнал с верхней частотой до 4000 Гц.

Классическим случаем является использование дифференциальной (разностной) ИКМ (ДИКМ, Differencial PCM, DPCM), когда вместо кодирования отсчетов, кодируют отклонение от предсказанного значения (сигнал ошибки, ошибка предсказания).

Рассмотренные выше методы могут вносить незначительные изменения и потери в речевые сигналы (например, сужение динамического диапазона в области высших частот, ограничение крутизны сигнала), которые практически не влияют на аутентичность речи.

2. Теоретические положения

Как известно, стандартная скорость передачи телефонии составляет 64кбит/с. Ее можно снизить, устраняя избыточность передаваемой информации. Наиболее простой метод — дифференциальное кодирование, когда вместо самого сигнала S(n) передают разность (ошибку) между сигналом S(n) и предсказанным его значением :

(1.1)

Идея дифференциального кодирования: можно не передавать то, что можно предсказать. А предсказать можно периодические процессы. Так, вместо передачи синусоиды по точкам, можно передать по каналу ее амплитуду и частоту, и при приеме эту синусоиду синтезировать.

В работе предсказателей используют алгоритм линейного предсказания:

(1.2)

Обычно, k≤ 8..10, так как при дальнейшем увеличении k точность предсказания не повышается.

Тогда:

(1.3)

Схема кодека дифференциальной ИКМ (ДИКМ) показана на рис. 1:

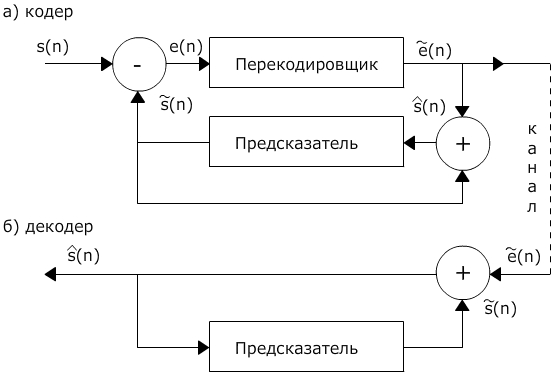
Рис. 1

Обычно ошибки e(n) оказываются на ниже самих отсчетов S(n), что позволяет несколько уменьшить число разрядов отсчетов e(n) в сравнении с разрядностью S(n). При этом падает и скорость передачи сигнала.

Основной проблемой при ДИКМ является оптимизация коэффициентов предсказателя, так как от их выбора зависят ошибки e(n).

3. Постановка задачи. Сжатие синусоидального сигнала с помощью дикм.

В ходе выполнения данной лабораторной работы необходимо промоделировать ситуации сжатия сигнала методами в 2-х случаях: сигнал представлен синусоидальным колебанием и непосредственно речевым сигналом. При этом следует определить, какие коэффициенты линейного предсказания являются оптимальными.

Пусть имеется исходный сигнал, изменяющийся по закону

(2.1)

где A= 0.5 и =10 Гц

Возьмем отсчеты этой синусоиды с частотой дискретизации 8000 Гц и квантуем полученные отсчеты 2048 уровнями (11 бит и 1 бит на знак). Получим последовательность входных отсчетов x(n), значения которых будем представлять в соответствующих уровнях квантования.

Определим значения предсказанных отсчетов как

(2.2)

Тогда разностный сигнал (сигнал ошибки), будет равен:

(2.3)

Благодаря выбору оптимальных коэффициентов a₁ и a₂ считаем, что полученные отсчеты разностного сигнала будут обладать разрядностью в два раза меньшей, чем отсчеты исходного. То есть значение разностного сигнала должно лежать в пределах от -31 до 31.Если же значение разностного сигнала превышает по модулю границы этих пределов, то в канал отправляем значение -31 или 31,в зависимости от знака е₁.

Следовательно, разностный сигнал e₂(n), передаваемый в канал, можно записать согласно (2.4):

(2.4)

Тогда на приемной стороне по значением предсказанного сигнала (2.5) и разностного сигнала e₂(n) получаем значение восстановленного сигнала(2.6):

(2.5)

(2.6)

Вышеописанный алгоритм реализуем при помощи технологии Matlab. Ниже приведен подробный листинг программы:

clear all;

a1=1.8;

a2=-0.8;

t=0.2;

Fs=8000;

A=1;

F=10;

Phi=0;

tm=0:1/Fs:t;

x=A*sind((F*360).*tm+Phi);

[x1,sh,kvbin,x]=DAC(x,Fs,t,12,2);

q = fft(x,Fs*t);

q = q(1:(Fs*t/2));

m = abs(q);

m1=m/(Fs*t/2);

f = (0:((Fs*t)-1)/2)/t;

tm=tm(1:Fs*t);

x=x(1:Fs*t);

for n=1:Fs*t

if n==1

pr_x(n)=0;

elseif n==2

pr_x(n)=round((a1*x(n-1)));

else

pr_x(n)=round(((a1*x(n-1)+a2*x(n-2))));

end

end

for n=1:Fs*t

if n==1

e(n)=x(n);

else

e(n)=x(n)-pr_x(n);

end

end

st=6;

for n=1:Fs*t

if e(n)>0

if e(n)>(2^(st-1))-1

e(n)=(2^(st-1))-1;

end

elseif e(n)<0

if e(n)<-((2^(st-1))-1)

e(n)=-((2^(st-1))-1);

end

end

end

diff=e;

diff_pr=e;

for n=1:Fs*t

if n==1

y(n)=e(n);

pr_y(n)=0;

elseif n==2

pr_y(n)=round((a1*y(n-1)));

y(n)=e(n)+pr_y(n);

else

pr_y(n)=round(((a1*y(n-1)+a2*y(n-2))));

y(n)=e(n)+pr_y(n);

end

diff(n)=((y(n)-x(n))^2)^0.5;

diff_pr(n)=pr_x(n)-pr_y(n);

end

dif_sr=0;

for i=1:Fs*t

dif_sr=dif_sr+diff_pr(n);

end

dif_sr=dif_sr/Fs*t;

error1=e;

error1(1)=0;

error=0;

e1(1)=e(1);

e1(2)=e(2);

for n=1:Fs*t

error=error+((x(n)-y(n))^2);

if n==1

error1(n)=((x(n)-y(n))^2);

else

error1(n)=error1(n-1)+((x(n)-y(n))^2);

end

end

%figure

%plot(tm,error1);

w = fft(e,Fs*t);

w = w(1:(Fs*t/2));

r = abs(w);

r1=r/(Fs*t/2);

f=f(1:20);

r1=r1(1:20);

m1=m1(1:20);

figure

plot (tm,y);

plot(tm,x,'b',tm,y,'--m',tm,e,'r','LineWidth',1.5)

title('Осцилограмма сигнала');% Подпись графика

xlabel('Время (с)'), grid on;% Подпись оси х графика

ylabel('Амплитуда'), grid on;% Подпись оси у графика

%figure

%plot(tm,pr_x,'b',tm,pr_y,'--m','LineWidth',1.5)

%title('Осцилограмма ПРЕДСКАЗАННОГО сигнала');% Подпись графика

%xlabel('Время (с)'), grid on;% Подпись оси х графика

%ylabel('Амплитуда'), grid on;% Подпись оси у графика

%figure

%plot(tm,diff_pr,'b','LineWidth',1.5)

%title('Осциллограмма разности предсказаний сигнала');% Подпись графика

%xlabel('Время (с)'), grid on;% Подпись оси х графика

%ylabel('Амплитуда'), grid on;% Подпись оси у графика

figure% Создаем новое окно

plot(f,m1,'r',f,r1,'b','LineWidth',1.5);

title('Спектр сигнала, красным спектр исходного сигнала, синим - разностного');% Подпись графика

xlabel('Частота (Гц)'), grid on;% Подпись оси х графика

ylabel('Амплитуда'), grid on;% Подпись оси у графика

%figure

%plot(tm,diff,'b','LineWidth',1.5);

%title('Осциллограмма разности сигналов');% Подпись графика

%xlabel('Время (с)'), grid on;% Подпись оси х графика

file_x=fopen('x_sinus.txt','wt');

for n=1:Fs*t;

fprintf(file_x,'%f\n', x(n));

end

fclose(file_x);

file_x=fopen('pr_x_sinus.txt','wt');

for n=1:Fs*t;

fprintf(file_x,'%f\n', pr_x(n));

end

fclose(file_x);

file_x=fopen('pr_y_sinus.txt','wt');

for n=1:Fs*t;

fprintf(file_x,'%f\n', pr_y(n));

end

fclose(file_x);

%

%

%

file_x=fopen('e_sinus.txt','wt');

for n=1:Fs*t;%

fprintf(file_x,'%f\n', e(n));

end

fclose(file_x);

file_x=fopen('y_sinus.txt','wt');

for n=1:Fs*t;

fprintf(file_x,'%f\n', y(n));

end

fclose(file_x);

Введенная подпрограмма “DAC” – подпрограмма квантователя. Ее листинг проиллюстрирован ниже:

function [kvant,sh,kvbin, kv]=DAC(x,Fs,t,n,sh)

%АЦП

if sh==2

xx=abs(x);

sh=max(xx)/2^(n-1);

else

xx=abs(x);

sh=sh;

end

for s0=1:Fs*t

i=2^(n-1)-1;

if x(s0)<0

for s1=1:2^(n-1)

if xx(s0)<i*sh

i=i-1;

else

if xx(s0)>(i+1)*sh-sh/2

kv(s0)=(i+1)*-1;

else

kv(s0)=i*-1;

end

end

end

elseif x(s0)>0

for s1=1:2^(n-1)

if xx(s0)<i*sh

i=i-1;

else

if xx(s0)>(i+1)*sh-sh/2

kv(s0)=(i+1);

%kvb(s0)=de2bi(i+1);

else

kv(s0)=i;

%kvb(s0)=de2bi(i);

end

end

end

elseif x(s0)==max(s0)

kv=i;

else

kv(s0)=0;

end

end

kvb=de2bi(abs(kv));

kvb1=zeros(Fs*t,n);

%for s3=1:Fs*t

% if x(s3)<0

% zn=0;

%

% else

% zn=1;

% end

% kvb1(s3,1)=de2bi(zn);

% lo=kvb(s3,:);

% kvb1(s3,2:n)= lo;

%end

kvant=kv*sh;

kvbin=kvb1;

end

Воспользовавшись вышеприведенной программой, будем изменять коэффициенты а₁ и а₂ таким образом, чтобы подобрать оптимальные коэффициенты для передачи синусоидального сигнала.

Представим полученные при этом спектрограммы и осциллограммы сигнала для различных пар коэффициентов а₁ и а_2.

Временные диаграммы отсчетов исходного сигнала (x), предсказанного на передающей стороне ( ), разностного (e), предсказанного на приемной стороне( ) и принятого сигнала (y), и спектрограммы этих сигналов, представлены ниже.

Эксперимент № 1

а₁=0.1 и а₂=-0.4

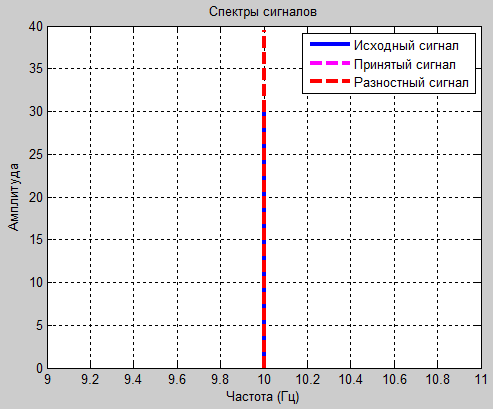
Рис. 2

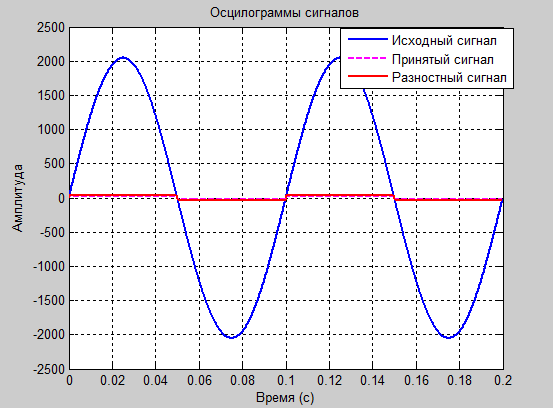
Рис. 3

Эксперимент № 2

а₁=0.1 и а₂=-0.8

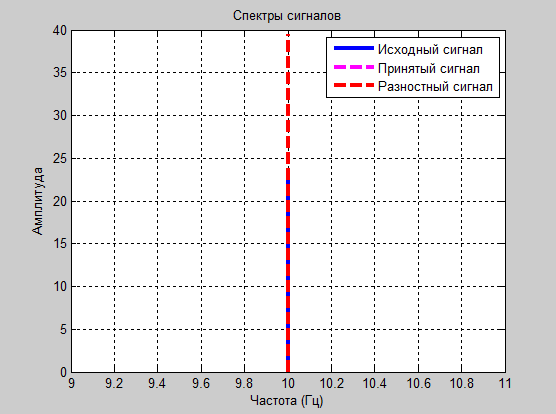
Рис. 4

Рис. 5

Эксперимент № 3

а₁=0.5 и а₂=-0.8

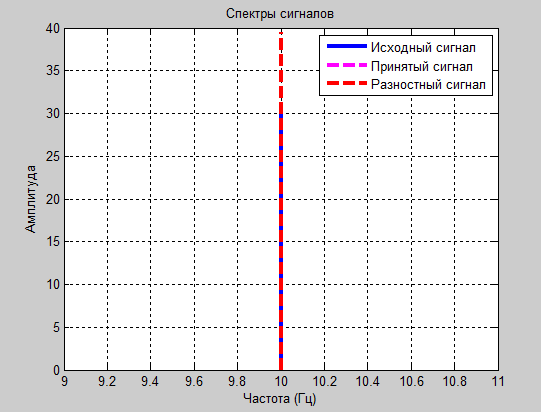
Рис. 6

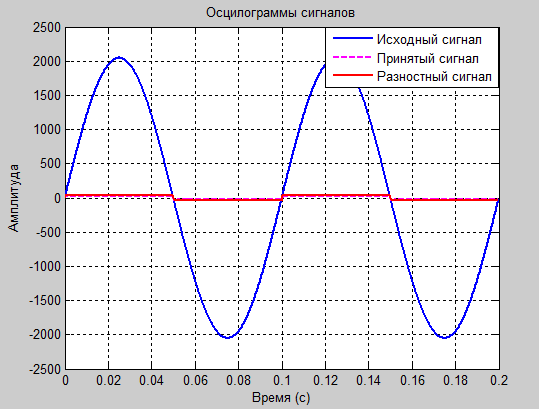
Рис. 7

Эксперимент № 4

а₁=1.4 и а₂=-0.8

Рис. 8

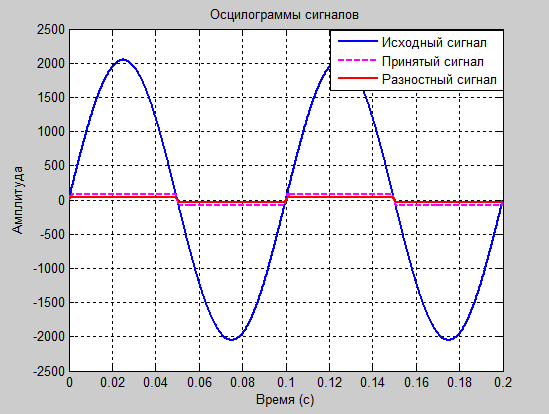
Рис. 9

Эксперимент № 5

а₁=1.8 и а₂=-0.8

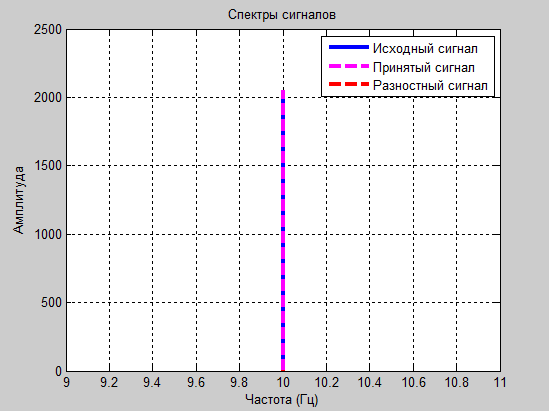
Рис. 10

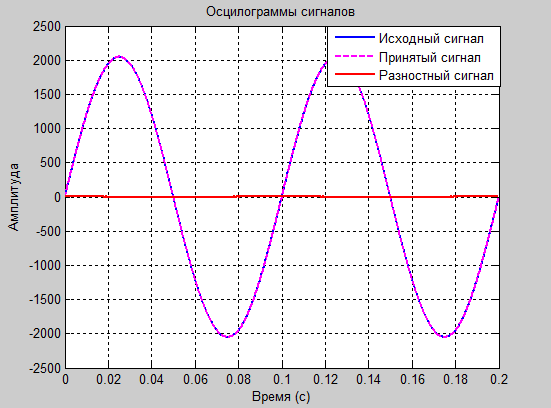
Рис. 11

Эксперимент № 6

а₁=1.8 и а₂=-0.9

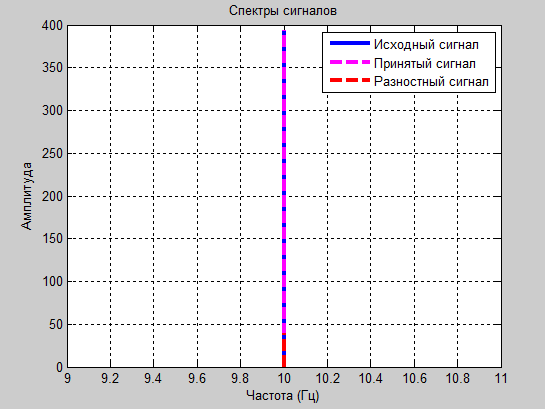
Рис. 12

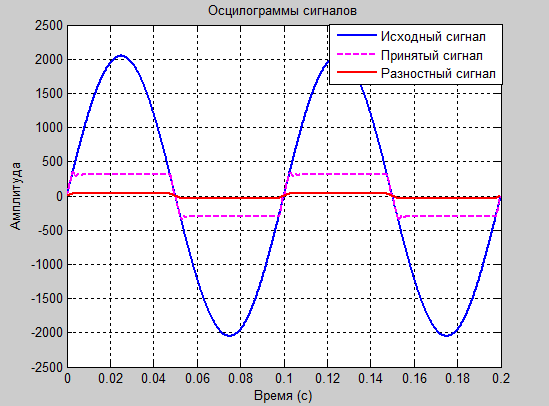
Рис. 13

Эксперимент № 7

а₁=1.8 и а₂=-1.2

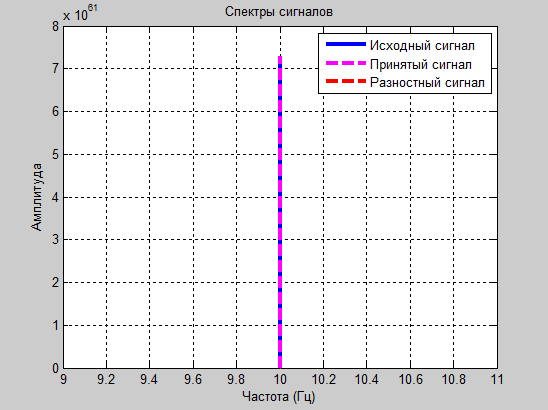
Рис. 14

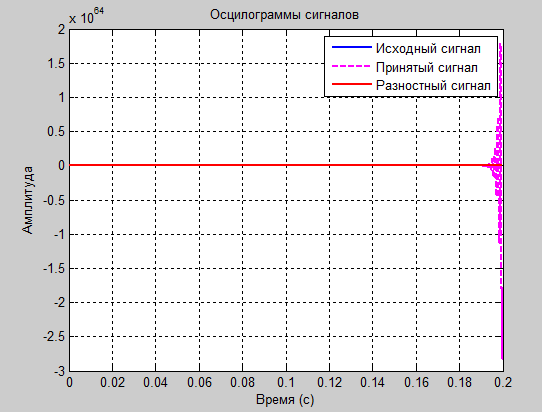
Рис. 15

Эксперимент № 8

а₁=2.2 и а₂=-0.8

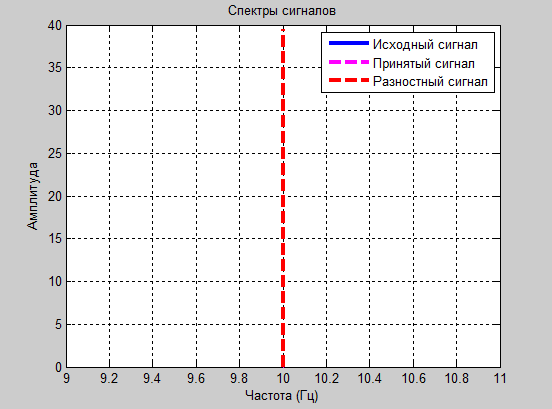
Рис. 16

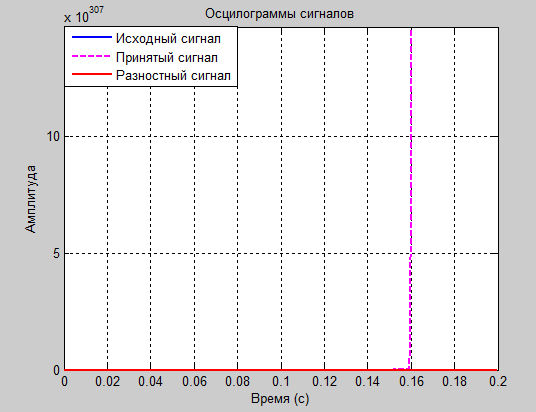
Рис. 17

Проанализировав полученные результаты: таблицы значений, осциллограммы и спектрограммы сигналов, следует сделать вывод о том, что оптимальными для передачи синусоидального сигнала являются коэффициенты а₁=1.8 и а₂= -0.8. Именно при этих значениях зможно передать разностный сигнал в пределах 6 бит и получить итоговый сигнал без заметных искажений.