Алгоритм сверточного декодирования Витерби

В 1967 году Витерби разработал и проанализировал алгоритм, в котором, по сути, реализуется декодирование, основанное на принципе максимального правдоподобия; однако в нем уменьшается вычислительная нагрузка за счет использования особенностей структуры конкретной решетки кода. Преимущество декодирования Витерби по сравнению с декодированием по методу “грубой силы”, заключается в том, что сложность декодера Витерби не является функцией количества символов в последовательности кодовых слов. Алгоритм включает в себя вычисление меры подобия (или расстояния), между сигналом, полученным в момент времени t1, и всеми путями решетки, входящими в каждое состояние в момент времени ti. В алгоритме Витерби не рассматривают те пути решетки, которые, согласно принципу максимального правдоподобия не могут быть оптимальными. Если в одно и то же состояние входят два пути, выбирается тот, который имеет лучшую метрику; такой путь называется выживающим. Отбор выживающих путей выполняют для каждого состояния. Таким образом, декодер углубляется в решетку, принимая решения путем исключения менее вероятных путей. Предварительный отказ от маловероятных путей упрощает процесс декоди­рования. В 1969 году Омура (Omura) показал, что основу алгоритма Витерби составляет оценка максимума правдоподобия. Отметим, что задачу отбора оптимальных путей можно выразить как выбор кодового слова с максимальной метрикой правдоподобия или минимальной метрикой расстояния.

Реализация декодера

В контексте решетчатой диаграммы, показанной на рис.3, переходы за один промежуток времени можно сгруппировать в 2v-1 непересекающиеся ячейки; каждая ячейка будет изображать четыре возможных перехода, причем v= К- 1 называется памятью кодера (encoder memory). Если К=3, то v = 2, и, следовательно, мы имеем 2v-1=2 ячейки. Эти ячейки показаны на рис. 4, где буквы а, b, с и d обозначают состояния в момент t1, а а', Ь', с’ и d’ — состояния в момент времени t1+1. Для каждого перехода изображена метрика ветви индексы которой означают переход из состояния х в состояние у. Эти ячейки и соответствующие логические элементы, которые корректируют метрики со­стояний {Гх}, представляют основные составляющие элементы декодера.

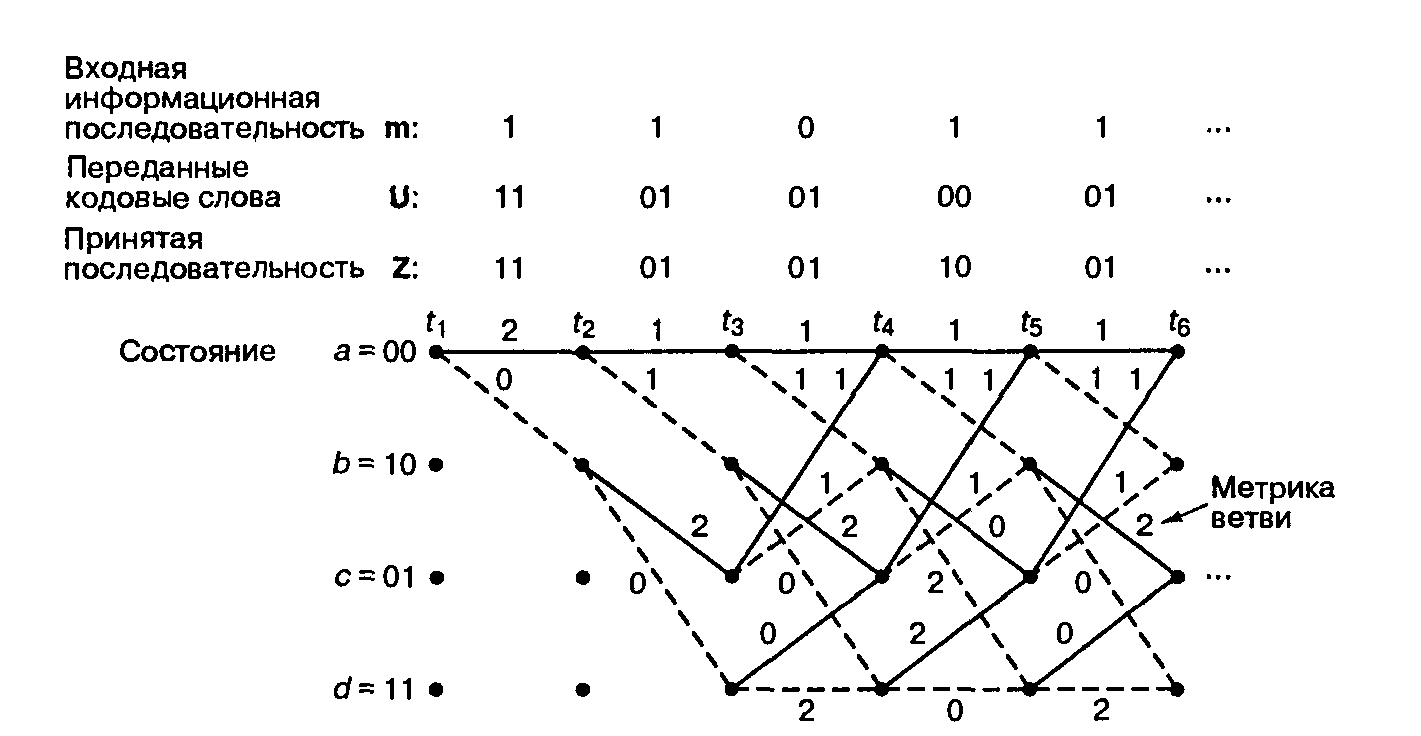
Рис.3. Решетчатая диаграмма декодера (степень кодирования ½, К=3)

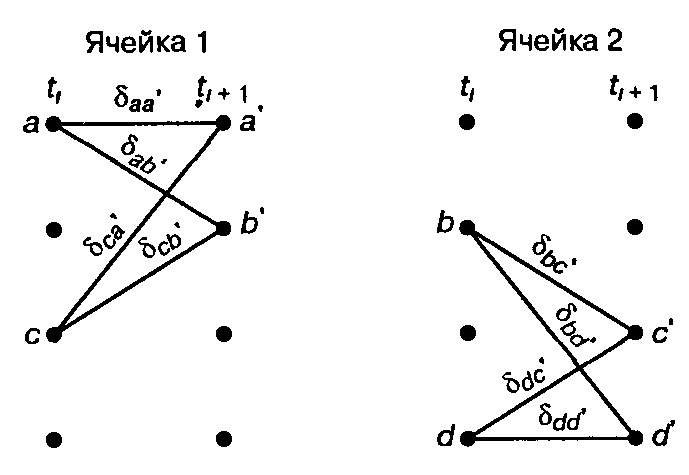
Рис.4. Примеры ячеек декодера

Мягкое декодирование по алгоритму Витерби

Для двоичной кодовой системы со скоростью кодирования 1/2 демодулятор подает на декодер два кодовых символа за один раз. Для жесткого (двухуровневого) декодирования каждую пару принятых кодовых символов можно изобразить на плоскости в виде одного из углов квадрата, как показано на рис. 6, а. Углы помечены двоичными числами (0, 0), (0, 1), (1, 0) и (1, 1), представляющими четыре возможных значения, которые могут принимать два кодовых символа в жесткой схеме принятия решений. Аналогично для 8-уровневого мягкого декодирования каждую пару кодовых символов можно отобразить на плоскости в виде квадрата размером 8x8, состоящего из 64 точек, как показано на рис. 6, б. В этом случае демодулятор больше не выдает жестких решений; он выдает квантованные сигналы с шумом (мягкая схема принятия решений).

Основное различие между мягким и жестким декодированием по алгоритму Витерби состоит в том, что в мягкой схеме не используется метрика расстояния Хэмминга, поскольку она имеет ограниченное разрешение. Метрика расстояний, которая имеет нужное разрешение, называется эвклидовым кодовым расстоянием, поэтому далее, чтобы облегчить ее применение, соответствующим образом преобразуем двоичные числа из единиц и нулей в восьмеричные числа от 0 до 7. Это можно видеть на рис. 6, в, где соответствующим образом обозначены углы квадрата; теперь для описания любой из 64 точек мы будем пользоваться парами целых чисел от 0 до 7. На рис. 6, в также изображена точка 5,4, представляющая пример пары значений ко­довых символов с шумом. Представим себе, что квадрат на рис. 6, в изображен в координатах (x, у). Каким будет евклидово кодовое расстояние между точкой с шумом 5,4 и точкой без шума 0,0? Оно равно

. А если мы захотим узнать евклидово кодовое расстояние между точкой с шумом 5,4 и точкой без шума 7,7? Аналогично .

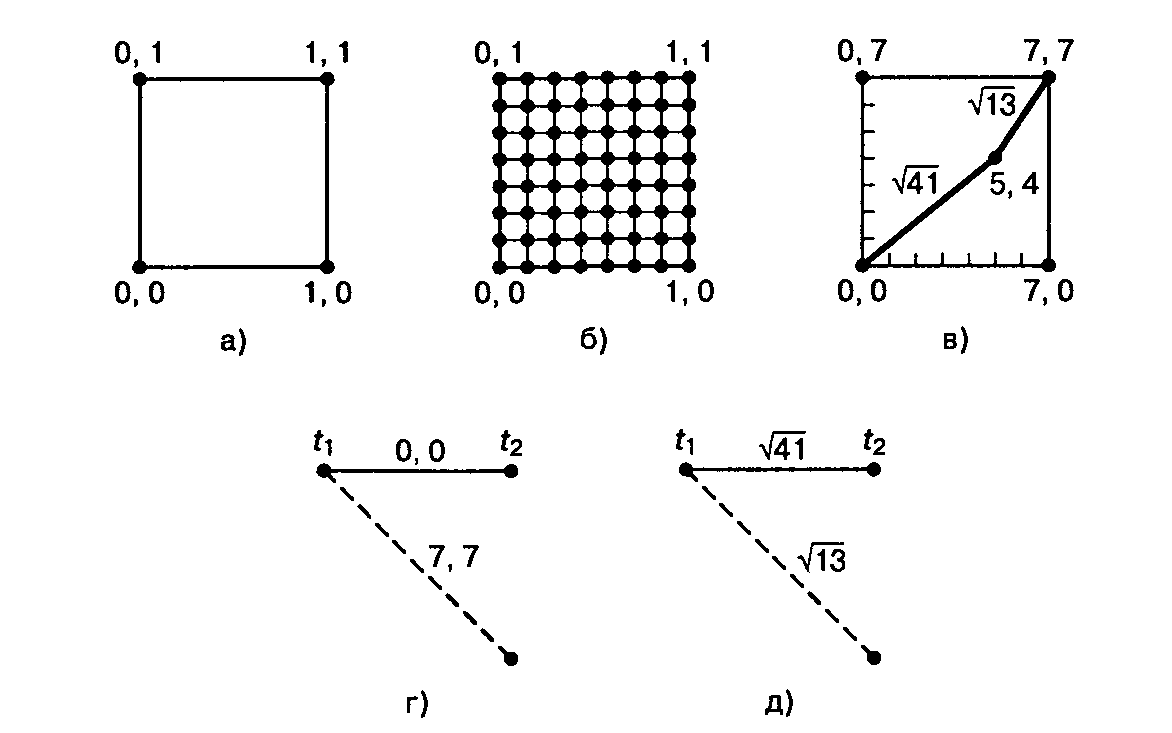
Рис.6. Декодирование Витерби: а) плоскость жесткой схемы принятия решений; б) 8-уровневая плоскость мягкой схемы принятия решений; в) пример мягких кодовых симво­лов; г) секция решетки кодирования, д) секция решетки декодирования

Мягкое декодирование по алгоритму Витерби, по большей части, осуществляся так же, как и жесткое. Единственное отличие состоит в том, что здесь не используется расстояние Хэмминга. Поэтому рассмотрим мягкое декодирование, осуществляемое с евклидовым кодовым расстоянием. На рис.(6 г) показана первая секция решетки кодирования, которая вначале имела вид, приведенный на рис.7. При этом кодовые слова преобразованы из двоичных в восьмеричные. Допустим, что пара кодовых символов, поступившая на декодер во время первого перехода, согласно мягкой схеме декодирования имеет значения 5,4. На рис. 6, д показана первая секция решетки декодирования. Метрика , представляющая евклидово кодовое расстояние между прибывшим кодовым словом 5,4 и кодовым словом 0,0, обозначена сплошной линией. Аналогично метрика представляет собой евклидово кодовое расстояние между поступившим кодовым символом 5,4 и ко­довым символом 7,7; это расстояние показано пунктирной линией. Оставшаяся часть задачи декодирования, которая сводится к отсечению решетки и поиску полной ветви, осуществляется аналогично схеме жесткого декодирования. Для этого  выбирают путь с максимальным весом, то есть евклидовым расстоянием. Заметим, что в реальных микросхемах, предназначенных для сверточного декодирования, евклидово кодовое расстояние в действительности не применяется, вместо него используют монотонную метрику, которая обладает сходными свойствами, но значительно проще в реализации. Примером такой метрики является квадрат евклидова кодового расстояния, в этом случае исключается рассмотренная выше операция взятия квадратного корня. Более того, если двоичные кодовые символы представлены биполярными величинами, тогда можно использовать метрику скалярного произведения. При такой метрике вместо минимального расстояния анализируют максимальные корреляции.

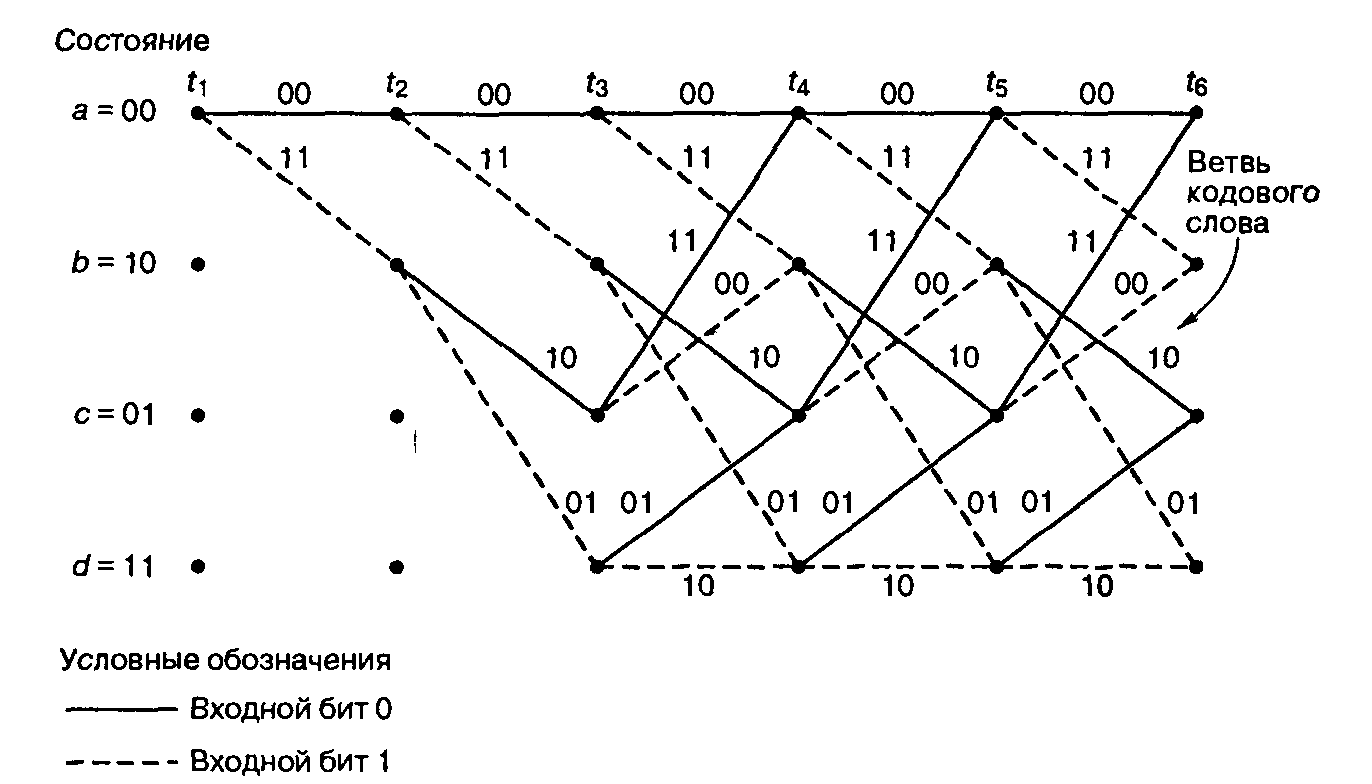
Рис.7.Решетчатая диаграмма кодера (степень квантования 1/2, К=3.