Задачи для контрольной работы №1

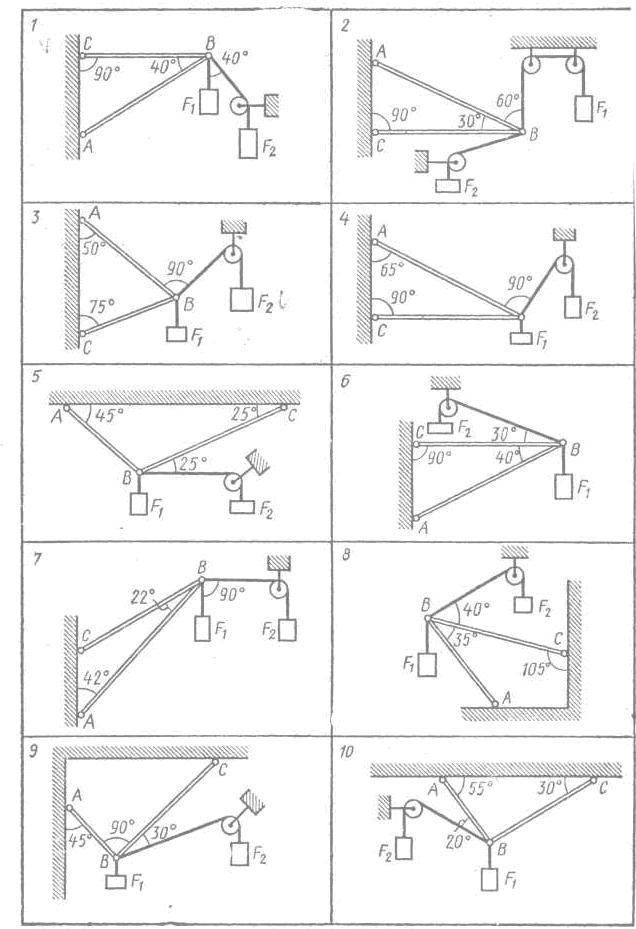
Задачи 1—10. Определить реакции стержней, удерживающих гру­зы F₁ и F₂. Массой стержней пренебречь. Схему своего варианта см. на рис. 3. Числовые данные своего варианта взять из табл. 1.

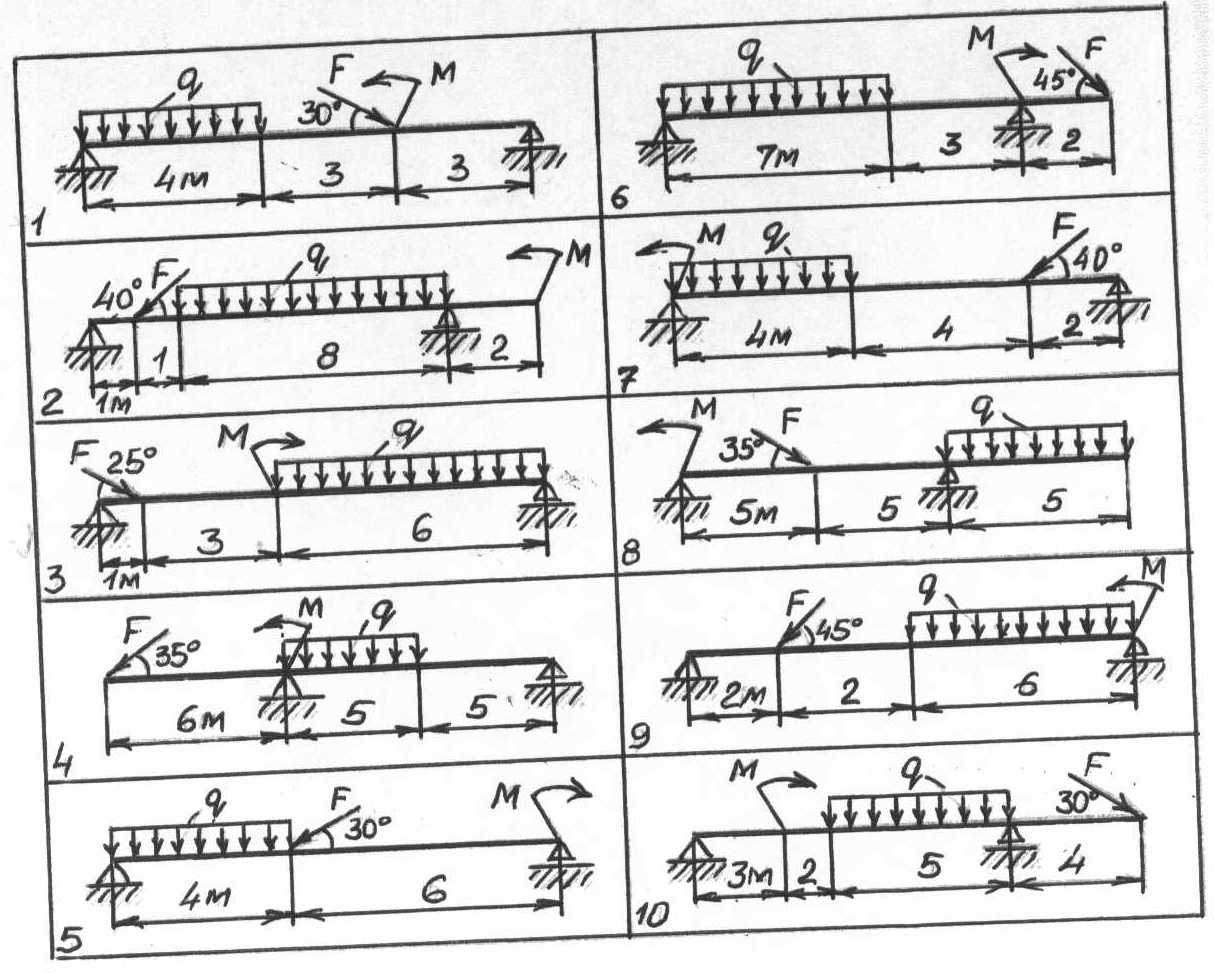
Задачи 11—20. Определить реакции опор двухопорной балки (рис. 4). Данные своего варианта взять из табл. 2.

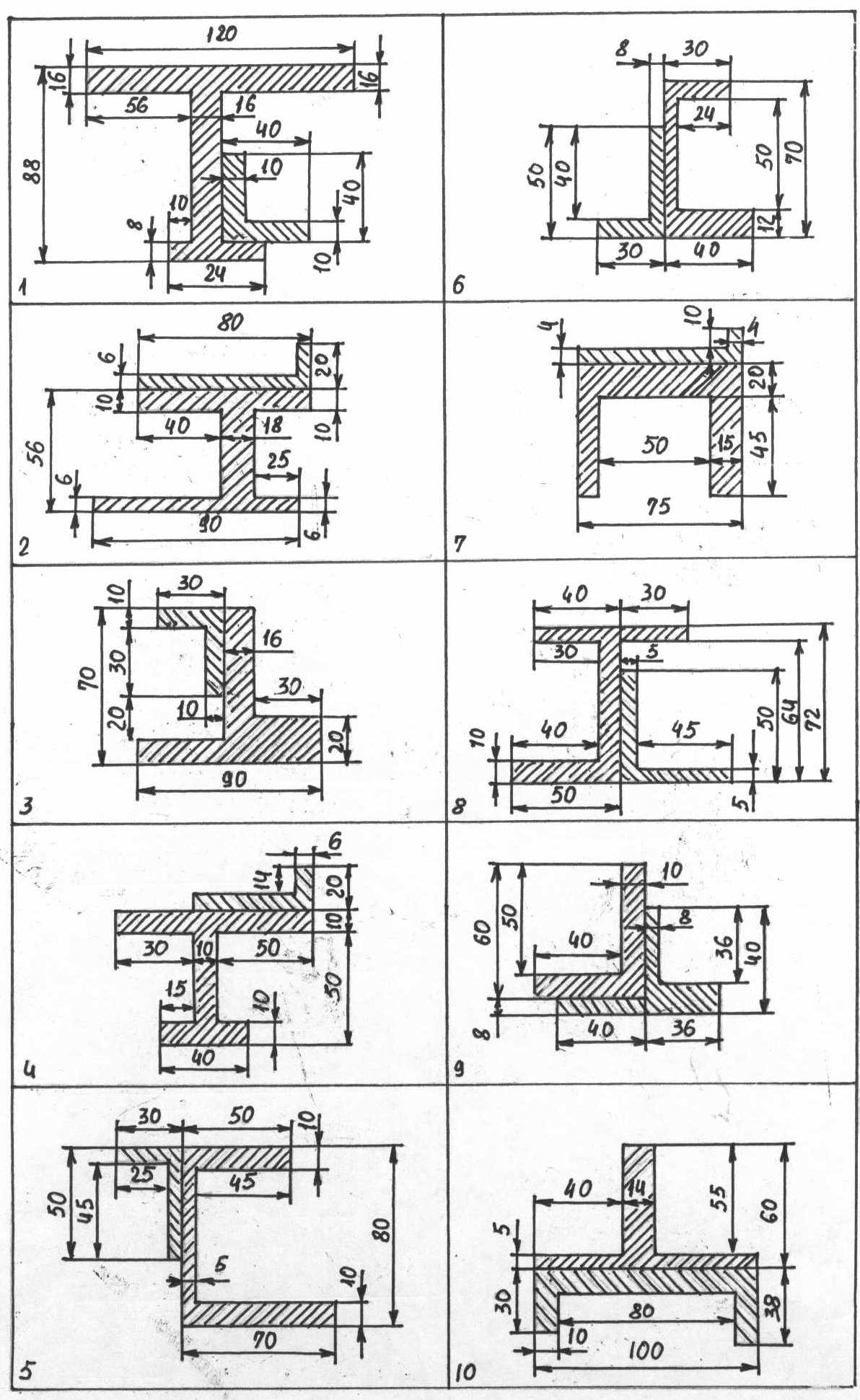
Задачи 31—40. Определить положение центра тяжести составно­го сечения, форма и размеры которого, в миллиметрах, показаны на рис. 5. Схему сечения для задачи своего варианта взять из табл. 3.

Таблица 1 (к задачам 1 – 10)

№ задачи и схемы на рис. 3										F1	F2
1	2	3	4	5	6	7	8	9	10
Варианты										кН
00	01	02	03	04	05	06	07	08	09	0,4	0,5
10	11	12	13	14	15	16	17	18	19	0,3	0, 8
20	21	22	23	24	25	26	27	28	29	0,6	0,4
30	31	32	33	34	35	36	37	38	39	0,2	0,5
49	40	41	42	43	44	45	46	47	48	0,5	0,8
59	58	57	56	55	54	53	52	51	50	0,8	0,4
62	60	63	61	66	64	67	65	69	68	0,4	0,2
70	75	71	76	72	77	73	78	74	79	0,8	1,2
80	85	81	86	82	87	83	88	84	89	0,8	1,0
90	91	92	93	94	95	96	97	98	99	0,9	0,6

Рисунок 3

Рисунок 4

Таблица 2 (к задачам 11 – 20)

№ задачи; № схемы на рис.4	Вариант	q	F	M	№ задачи; № схемы на рис.4	Вариант	q	F	M
		Н/м	Н	Н∙м			Н/м	Н	Н∙м
11; 1	00	5	40	10	12; 2	01	1	60	54
	11	2	25	20		12	4,5	20	85
	22	10	16	14		23	2	15	40
	33	1,5	50	30		34	5	2,5	100
	45	6	82	60		46	3,5	40	55
	50	3	15	25		51	6	35	60
	66	8	45	40		67	3	100	90
	71	4,5	18	10		72	1,5	80	20
	84	1	20	25		88	8	30	75
	99	12	54	35		90	10	50	30

Продолжение табл. 2 (к задачам 11 – 20)

№ задачи; № схемы на рис.4	Вариант	q	F	M	№ задачи; № схемы на рис.4	Вариант	q	F	M
		Н/м	Н	Н∙м			Н/м	Н	Н∙м
13; 3	02	5	80	25	14; 4	03	4	10	8
	13	2,5	15	10		14	1	12	10
	24	4	30	20		25	12	16	15
	35	10	55	40		36	8	20	12
	47	12	10	15		48	2	5	3
	52	8	100	30		53	14	30	24
	68	4,5	65	45		69	6	25	20
	73	2	85	60		74	10	8	6
	80	6	90	18		85	16	4	12
	91	3,5	20	16		92	20	15	8
15; 5	04	5	50	35	16; 6	05	8	12	20
	15	4,5	35	30		16	3,5	10	45
	26	8	25	20		27	0,5	8	10
	37	1,5	10	8		38	10	15	50
	49	2,5	65	50		40	15	18	30
	54	10	8	25		55	4,5	20	15
	60	12	16	40		61	8	3	25
	75	15	30	28		76	12	5	18
	81	5,5	12	15		86	8,5	12	30
	93	6	55	45		94	6	4	45
17; 7	06	2	50	35	18; 8	07	4	18	15
	17	4	10	5		18	6,5	24	20
	28	6	12	8		29	10	16	12
	39	8	15	50		30	2,5	20	25
	41	12	80	15		42	12	40	50
	56	10	35	25		57	3	35	65
	62	20	40	30		63	8	10	25
	77	14	25	20		78	1,5	12	90
	82	16	14	65		87	1	60	35
	95	30	65	75		96	5	15	10
19; 9	08	4	15	2	20; 10	09	4	50	10
	19	1,5	40	15		10	6	65	8
	20	1	20	18		21	2	80	100
	31	10	16	25		32	18	10	15
	43	5	18	14		44	20	55	150
	58	8	10	35		59	10	30	45
	64	6	25	20		65	16	10	25
	79	12	40	30		70	8	2	40
	83	3	35	15		88	14	6	10
	97	7	12	10		98	30	50	60

Рисунок 5

Таблица 3 (к задачам 31-40)

№ задачи	31	32	33	34	35	36	37	38	39	40
№ схемы	1	2	3	4	5	6	7	8	9	10

Две следующие задачи каждого варианта могут быть решены из усвоения тем «Основные положения сопротивления материалов» и «Растяжение и сжатие». Прежде чем приступить к их решению, учащийся должен научиться безукоризненно владеть методом сечений для определения внутренних силовых факторов. Эти навыки пригодятся учащимся для выполнения всех остальных задач.

Четвертая задача (задачи 61—70) требует от учащегося уметь строить эпюры продольных сил, нормальных напряжений и определять удлинения или укорочения бруса.

При работе бруса на растяжение и сжатие в его поперечных сечениях возникает продольная сила N. Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на его продольную ось всех внешних сил, действующих на отсеченную часть.

Для расчета на прочность и определения, перемещений необходимо знать закон изменения продольных сил по его длине, Правило знаков: при растяжении продольная сила положительна, при сжатии - отрицательна. Условие прочности при растяжении имеет вид

где , N — соответственно нормальное напряжение и продольная сила в опасном сечении (т.е. в сечении, где возникают наибольшие напряжения); А — площадь поперечного сечения; [] — допускаемое напряжение. Исходя из условия прочности, можно решать три вида задач: 1) проверка прочности; 2) подбор сечения A>N / []; 3) определение допускаемой нагрузки [N]< []А.

Последовательность решения задачи:

1. Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и места изменения размеров поперечного сечения.

2. Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N) и построить эпюру продольных сил N. Проведя параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.

3. Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пре­делах каждого участка напряжения постоянны, т.е. эпюра на дан­ном участке изображается прямой, параллельной оси бруса.

4. Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.

Рисунок 6

Пример 3. Для данного ступенчатого бруса (рис. 6, а) по­строить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца, если Е = 210⁵ МПа =210¹¹ Па; F₁ = 30 кН; F₂ = 38 кН; F₃ = 42 кН; А₁ = 1,9 см²; А₂ = 3,1 см² .

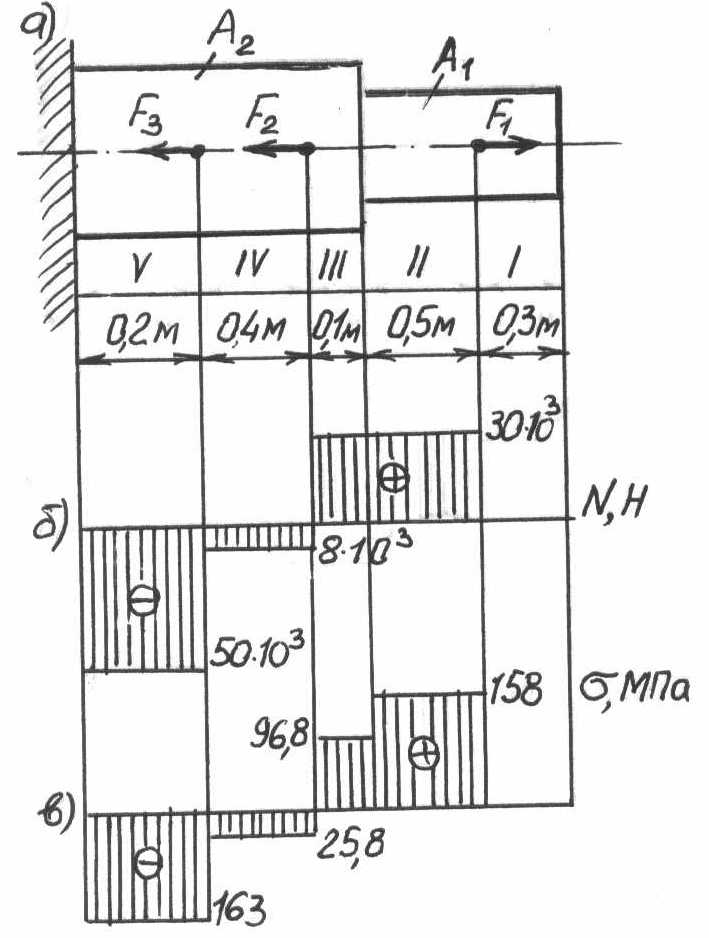
Решение:

1. Разбиваем брус на участки, как показано на рис. 6, а.

2. Определяем ординаты эпюры X на участках бруса:

Строим эпюру продольных сил (рис. 6, б).

3. Вычисляем ординаты эпюры нормальных напряжений:

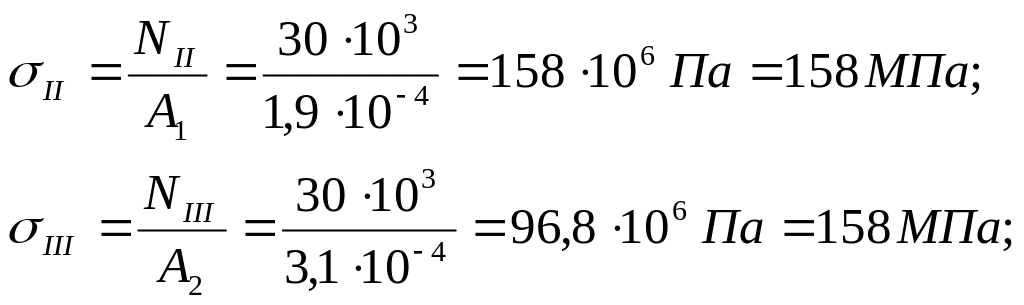
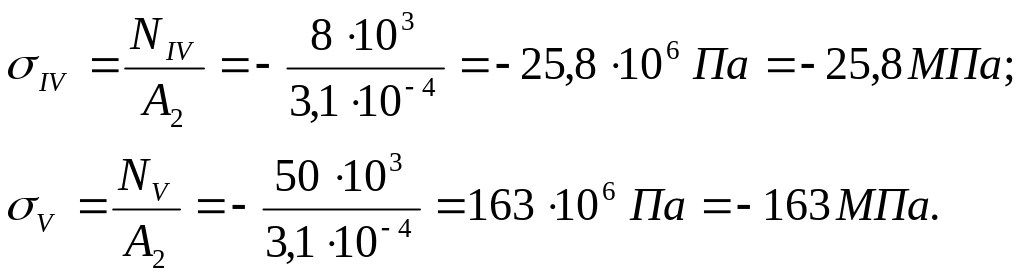
Строим эпюру нормальных напряжений (рис. 6, в).

3. Определяем перемещение свободного конца:

;

;

;

.

Пятая задача (задачи 81—90). К решению этой задачи следу­ет приступить после изучения темы «Кручение».

Кручением называют такой вид иагружения бруса, при кото­ром в его поперечных сечениях возникает только одни внутренний силовой фактор — крутящий момент М_к (или М_г).

Крутящий момент в произвольном поперечном сечении бруса равен алгебраической сумме внешних моментов, действующих на от­сеченную часть: М_к= М_i (имеет­ся в виду, что плоскости действия всех внешних скручивающих мо­ментов M_i перпендикулярны про­дольной оси бруса).

Рис. 7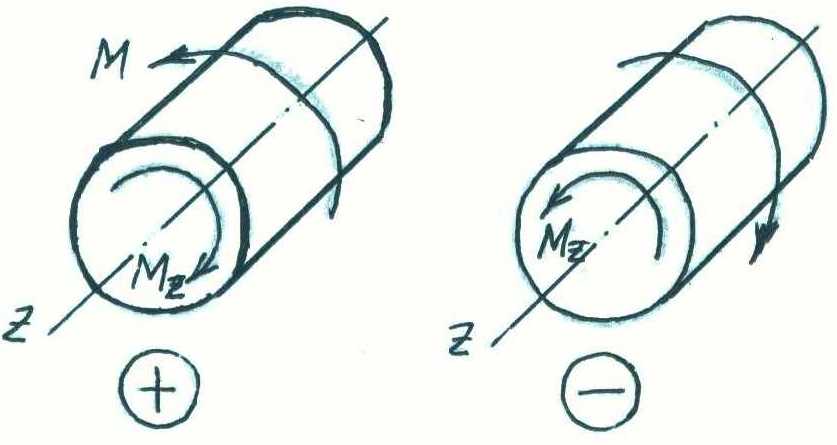

Б удем считать крутящий мо­мент положительным, если для на­блюдателя, смотрящего на прове­денное сечение, он представляется направленным по часовой стрелке. Соответствующий внешний мо­мент направлен против часовой стрелки (рис. 7).

В пятой задаче необходимо выполнить проектный расчет ва­ла круглого поперечного сечения из условий прочности и из усло­вий жесткости; из двух полученных значений диаметров следует выбрать наибольшее значение.

Последовательность решения задачи:

1. Определить внешние скручивающие моменты по формуле М=Р/, где Р— мощность,  — угловая скорость.

2. Определить уравновешивающий момент, используя уравнение равновесия  М = 0, так как при равномерном вращении вала алгебраическая сумма приложенных к нему внешних скручивающих (вращающих) моментов равна нулю.

3. Пользуясь методом сечений, построить эпюру крутящих моментов по длине вала.

4. Для участка вала, в котором возникает наибольший крутя­щий момент, определить диаметр вала для круглого сечения из ус­ловий прочности и жесткости. Из двух полученных диаметров вала выбрать наибольший.

П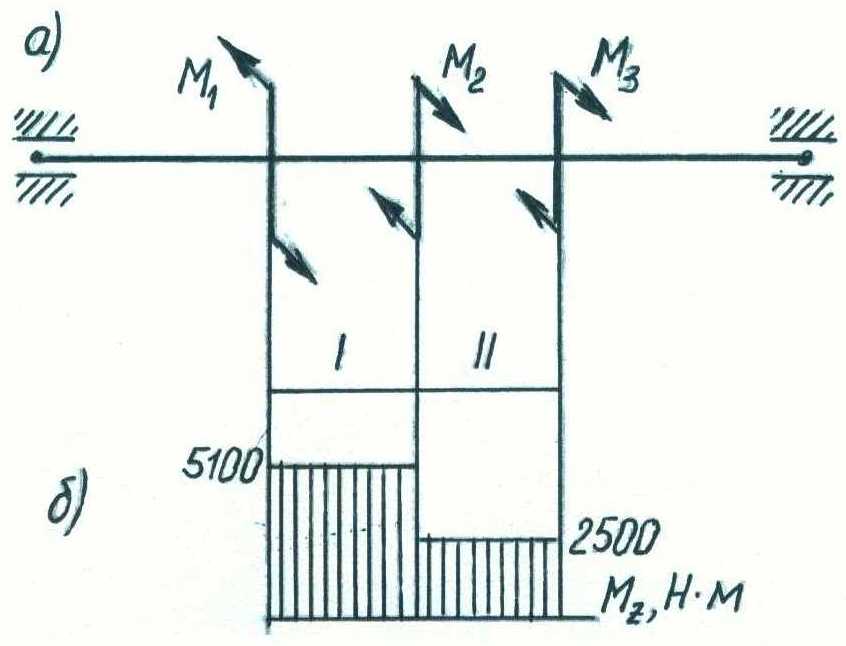 ример 4. Для стального вала (рис. 8, а) круглого поперечного сечения постоянного по длине требуется:

1. Определить значения моментов М₂ и М₃, соответствующие передаваемым мощностям Р₂ и Р₃, а также уравновешивающий момент M₁.

2. Построить эпюру крутящих моментов.

3. Определить требуемый диаметр вала из расчетов на прочность и жесткость, если [_к] = 30 МПа; [₀]=0,02рад/м; Р₂ =52 кВт; Р₃ = 50 кВт;  = 20 рад/с; G = 810⁴ МПа.

Окончательное значение диаметра округлить до ближайшего четного (или оканчивающего на пять) числа.

Решение:

1. Определяем величины внешних скручивающих моментов

Рисунок 8

.

2. Определяем уравновешивающий момент :

;

3. Строим эпюру (рис. 8,б)

4. Определяем диаметр вала из условий прочности и жесткости.

(рис. 8,б)

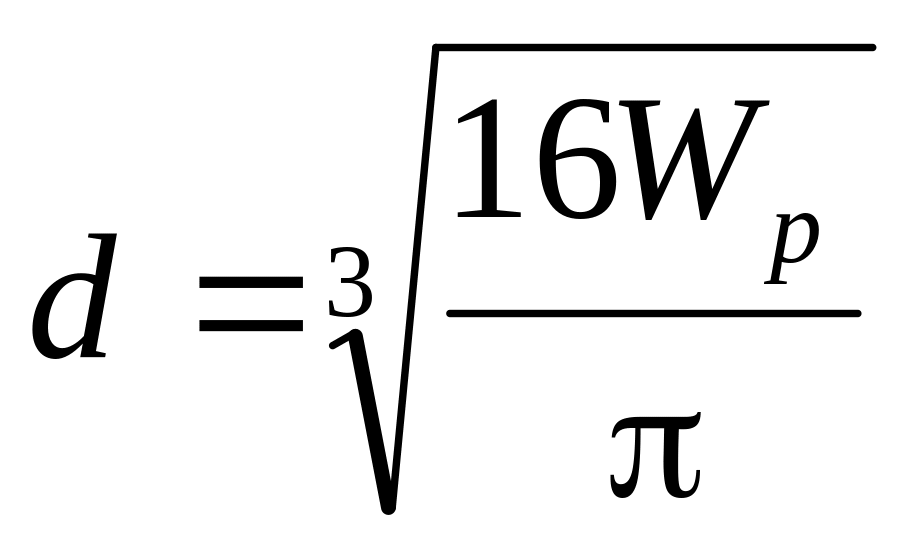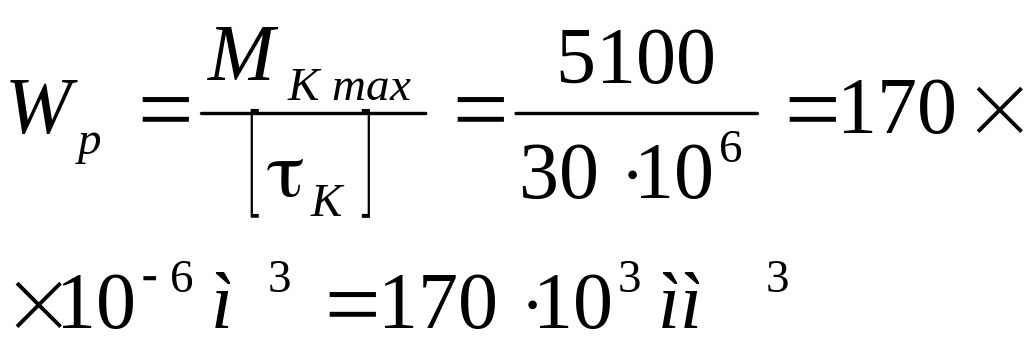
Из условий прочности: ,где Принимаем

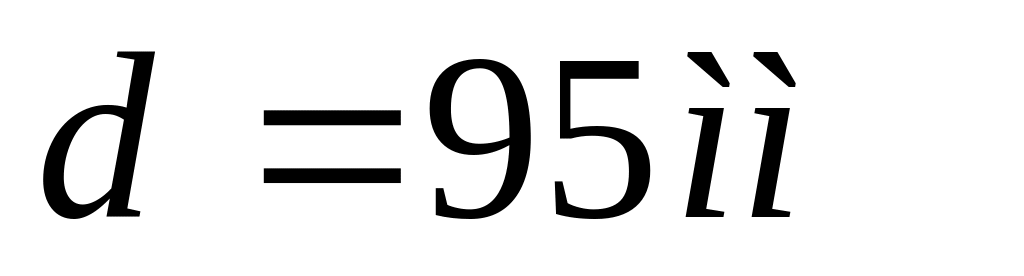
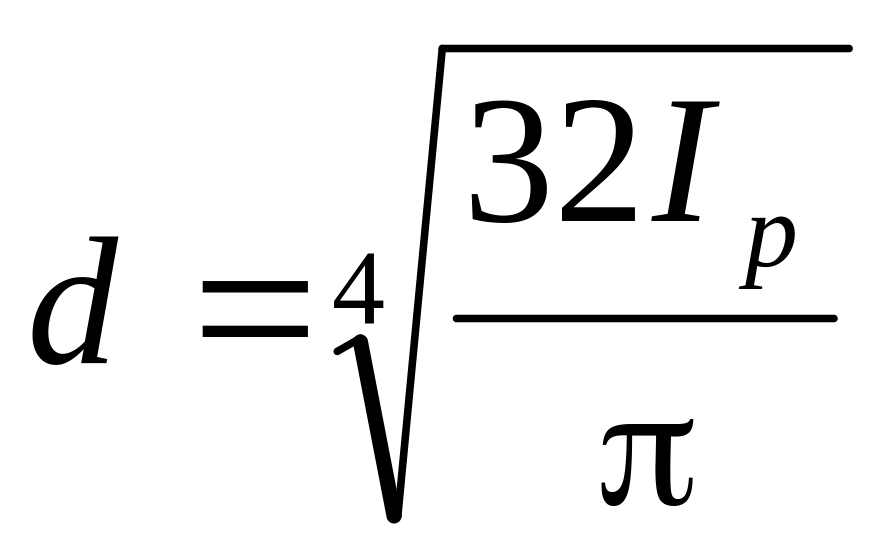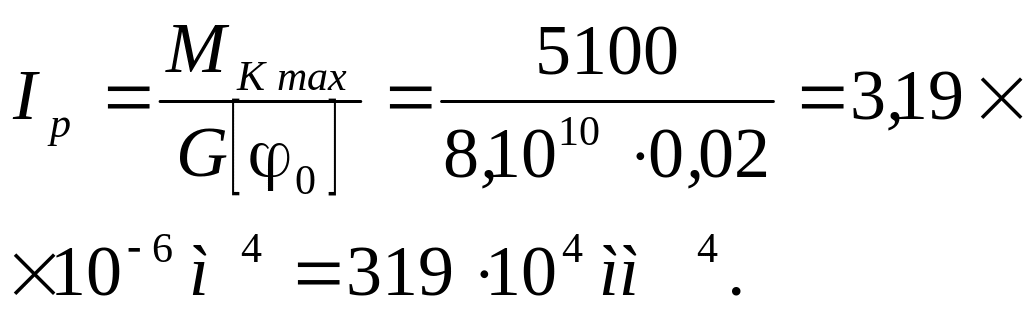
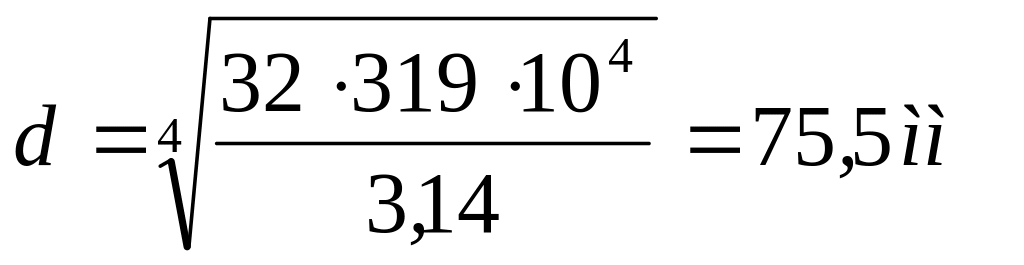
Из условий жесткости: , где Принимаем

Требуемый размер сечения получился больше из расчета на прочность, поэтому его принимаем как окончательный: d=95 мм.

Шестая задача (задачи 91—100). К решению этой задачи следует приступить после изучения темы «Изгиб». Изгиб — это та­кой вид деформации бруса, при котором в его поперечных сечени­ях возникают изгибающие моменты. В большинстве случаев одно­временно с изгибающими моментами возникают и поперечные си­лы; такой изгиб называют поперечным; если поперечные силы не возникают, изгиб называют чистым. Изгибающий момент М_и в про­извольном поперечном сечении бруса численно равен алгебраичес­кой сумме моментов внешних сил, действующих на отсеченную часть, относительно центра тяжести сечения: М_и= М. Поперечная сила в произвольном поперечном сечении бруса численно равна алгебра­ической сумме внешних сил, действующих на отсеченную часть: Q = F. Причем все внешние силы и моменты действуют в главной продольной плоскости бруса и расположены перпендикулярно про­дольной оси бруса.

Правило знаков для поперечной силы: силам, поворачивающим отсеченную часть балки относительно рассматриваемого сечения по ходу часовой стрелки, приписывается знак плюс, а си­лам, поворачивающим отсеченную часть балки относительно рас­сматриваемого сечения против хода часовой стрелки, приписывается знак минус.

П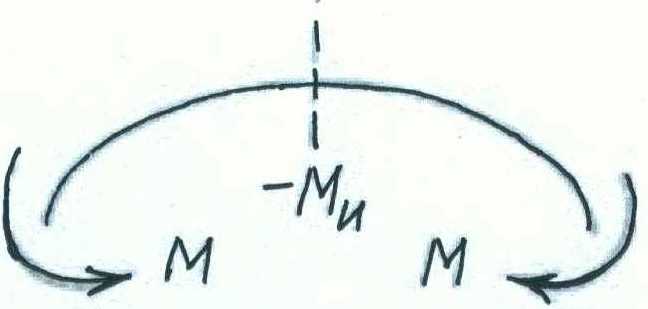 равило знаков для изгибающих моментов: внешним моментам, изгибающим мысленно закрепленную в рассматриваемом сечении от­сеченную часть бруса выпуклостью вниз, приписывается знак плюс, а моментам, изгибающим отсеченную часть бруса вы­пуклостью вверх,— знак минус (рис. 9).Между выражениями изгибающего момента M_и поперечной силы Q_v и интенсивностью распределенной нагрузки q существуют дифференциальные зависимости. На основе метода сечений и дифференци­альных зависимостей устанавливается вза­имосвязь эпюр М_х и Q_y между собой и с внешней нагрузкой, поэтому достаточно вычислить ординаты эпюр для характерных сечений и соединить их линиями. Характер­ными являются сечения балки, где приложены сосредоточенные си­лы и моменты (включая опорные сечения), а также сечения, ограни­чивающие участки с равномерно распределенной нагрузкой. Приведем некоторые правила построения эпюр.

Для эпюры поперечных сил:

1. На участке, нагруженном равномерно распределенной нагруз­кой, эпюра изображается прямой, наклоненной к оси балки.

2. На участке, свободном от распределенной нагрузки, эпюра изображается прямой, параллельной оси балки.

3. В сечении балки, где приложена сосредоточенная пара сил, поперечная сила не изменяет своего значения.

4. В сечении, где приложена сосредоточенная сила, эпюра поперечных сил меняется скачкообразно на значение, равное прило­женной силе.

5. В концевом сечении балки поперечная сила численно равна сосредоточенной силе (активной или реактивной), приложенной в этом сечении. Если в концевом сечении балки не приложена сосре­доточенная сила, то поперечная сила в этом сечении равна нулю.

Для эпюры изгибающих моментов.

1. На участке, нагруженном равномерно распределенной наг­рузкой, эпюра моментов изображается квадратичной параболой. Выпуклость параболы направлена навстречу нагрузке.

2. На участке, свободном от равномерно распределенной нагрузки, эпюра моментов изображается прямой линией.

3. В сечении балки, где приложена сосредоточенная пара сил, изгибающий момент меняется скачкообразно на значение, равное моменту приложенной пары.

4. Изгибающий момент в концевом сечении балки равен нулю, если в нем не приложена сосредоточенная пара сил. Если же в кон­цевом сечении приложена активная или реактивная пара сил, то изгибающий момент в этом сечении равен моменту приложенной пары.

5. На участке, где поперечная сила равна нулю, балка испытывает чистый изгиб, и эпюра изгибающих моментов изображается прямой, параллельной оси балки.

6 Изгибающий момент принимает экстремальное значение в се­чении, где эпюра поперечных сил проходит через нуль, меняя знаки с «+ » на «—» или с «—» на « + ».

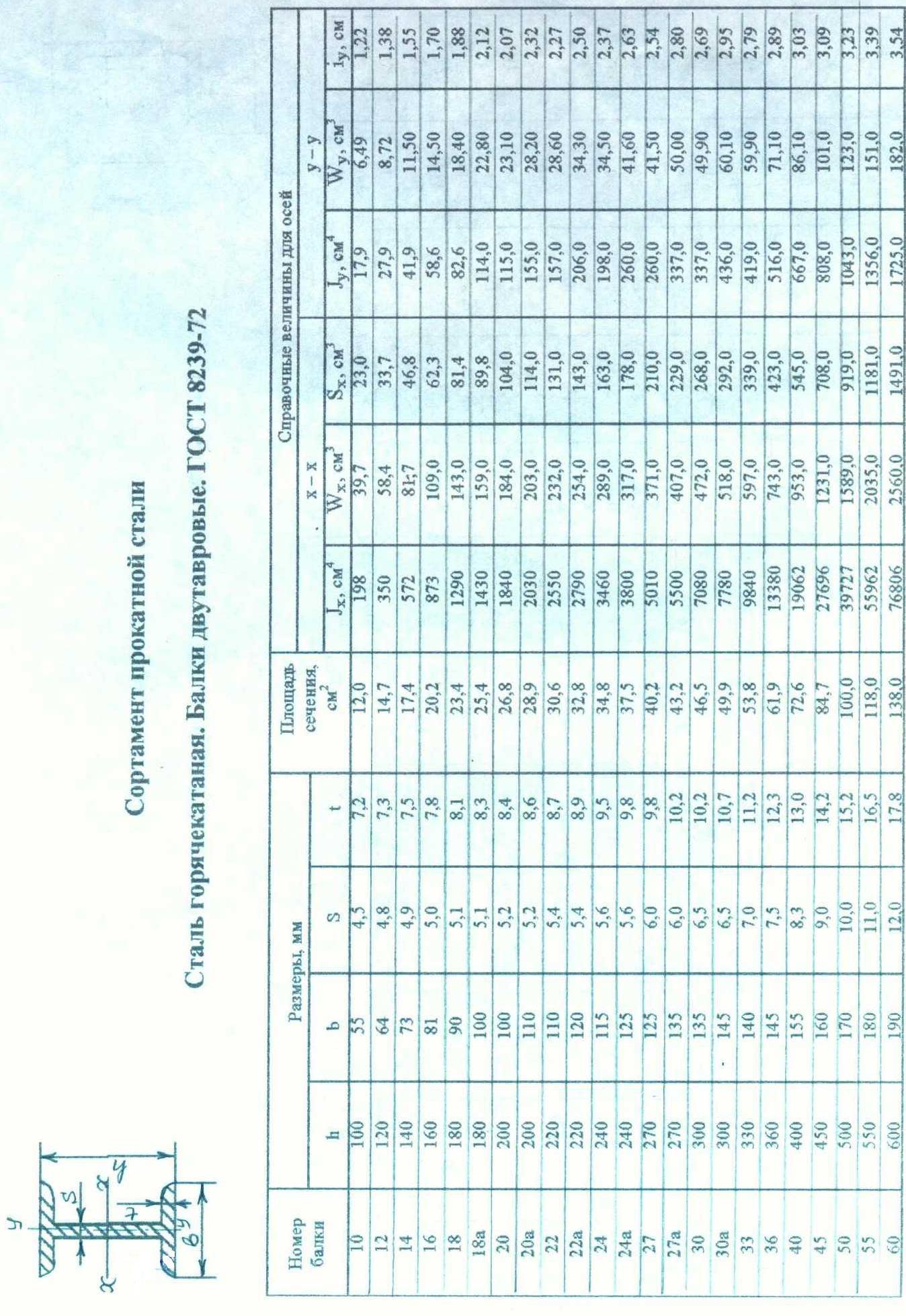
В рассматриваемой задаче требуется построить эпюры попереч­ных сил и изгибающих моментов, а также подобрать размеры по­перечного сечения балки, выполненной из прокатного профиля — двутавра.

Условие прочности для балок с сечениями, симметричными отно­сительно нейтральной оси, имеет вид

где W_x— осевой момент сопротивления сечения.

Для подбора сечения балки (проектного расчета) из условия прочности определяют необходимое значение осевого момента со­противления. По найденному моменту сопротивления W_x подбирают соответству­ющее сечение по сортаменту (см. приложение 1).

Для закрепленной одним концом балки расчет целесообразно вести со свободного конца (чтобы избежать определения опорных реакций в заделке).

Последовательность решения задачи:

1. Балку разделить на участки по характерным точкам.

2. Определить вид эпюры поперечных сил на каждом участке в зависимости от внешней нагрузки, вычислить поперечные силы в характерных сечениях и построить эпюру поперечных сил.

3. Определить вид эпюры изгибающих моментов на каждом участке в зависимости от внешней нагрузки, вычислить изгибающие моменты в характерных сечениях и построить эпюру изгибающих моментов. Для определения экстремальных значений изгибающих моментов дополнительно определить моменты в сечениях, где эпюра поперечных сил проходит через нуль (в примере 5— сечение К).

4. Для подбора сечения из условия прочности определить W_x в опасном сечении, т.е. в сечении, где изгибающий момент имеет наибольшее по модулю значение.

Пример 5. Для заданной консольной балки (поперечное сече­ние—двутавр, [] = 160 МПа) построить эпюры Q_y и М_х и подо­брать сечение по сортаменту.

1. Делим балку на участки по характерным точкам О, В, С, D (рис. 10, а)

2. Определяем ординаты и строим эпюру (рис. 10,б):

;

3. Определяем ординаты и строим эпюру (рис. 10, в):

Для определения экстремального значения момента в сечении К , где , определяем длину КВ.

подобен (рис.10, б), отсюда:

4. Исходя из эпюры (рис.10, в):

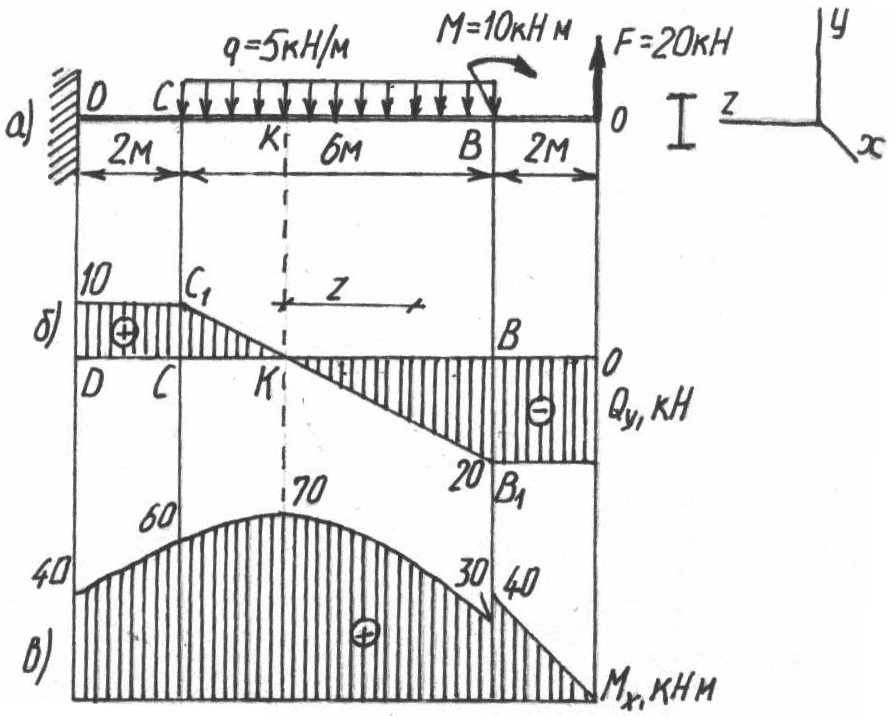В соответствии с ГОСТ 8239-72 выбираем двутавр №30. (см. приложение1)

Задачи 61 – 70. Двухступенчатый стальной брус, длины ступеней которого указаны на рис. 11 (схемы 1-10), нагружен силами Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение свободного конца бруса, приняв . Числовые значения , а также площади поперечных сечений ступеней и для своего варианта взять из табл. 4.

Рисунок 10

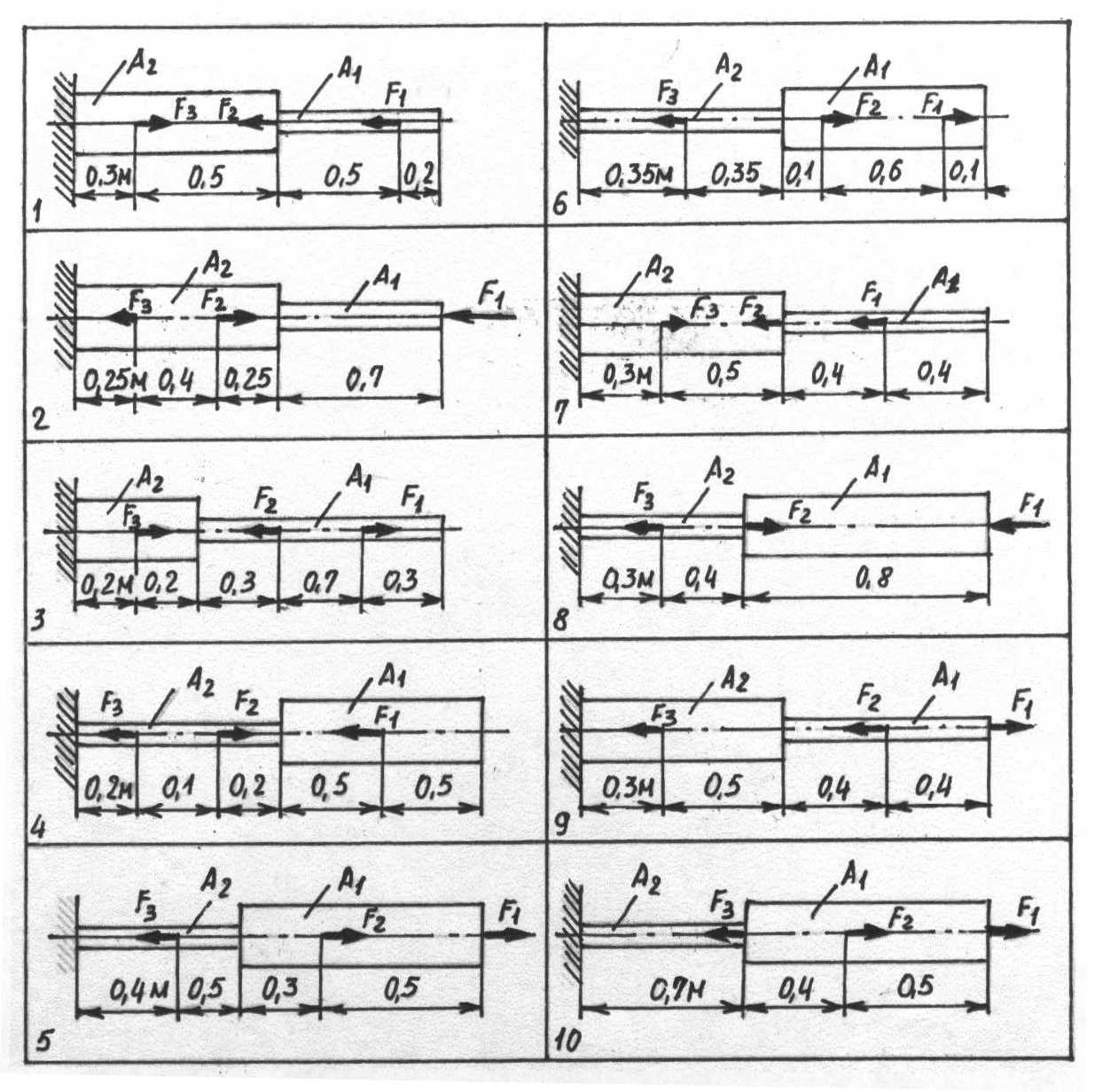
Рисунок 11

Задачи 71-73. Для данного двухступенчатого бруса, размеры которого показаны на рис. 12 (схемы 1,2,3), раскрыть статическую неопределимость, построить эпюры продольных сил и нормальных напряжений по длине бруса и определить, на сколько процентов перегружен или недогружен брус в опасном сечении. Принять

Задачи 74 – 78. Определить из условия прочности допускаемое значение силы для заданного стального бруса постоянного поперечного сечения (рис. 12, схемы 4,5,6) определив допускаемое значение силы , построить по длине бруса эпюры продольных сил и нормальных напряжений. Принять

Задачи 77, 78. Из условия прочности определить размер поперечного сечения стальных стержней (рис 12, схемы 7,8), удерживающих в равновесии абсолютно жесткий брус, шарнирно закрепленный концом, если Определив площадь А, найти напряжения в поперечных сечениях стержней.

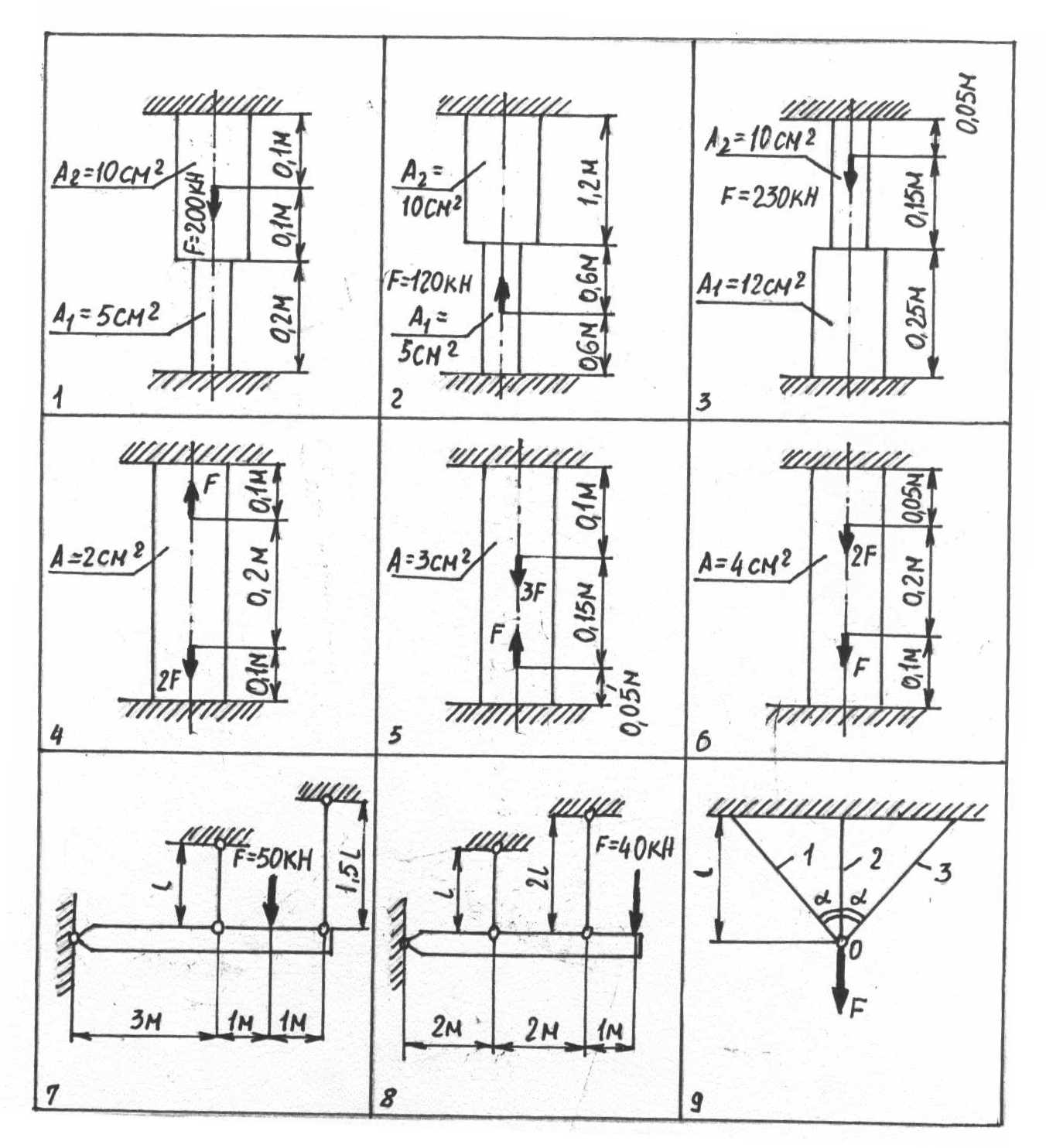
Рисунок 12

Задачи 79, 80. Конструкция, состоящая из трех стальных стержней, соединенных шарнирно, нагружено силой (рис. 12, схема 9), все стержни имеют одну и ту же площадь поперечного сечения А. Принять В задаче 79 определить силы в стержнях и найти площадь поперечного сечения А из условия прочности. В задаче 80 определить силы в стержнях и перемещение шарнира О. Для задачи 79: Для задачи 80:

Задачи 81 – 90. Для стального вала постоянного поперечного сечения (рис. 13 схемы 1 – 10): 1) определить значение моментов 2) Построить эпюру крутящих моментов; 3) определить диаметр вала из расчетов на прочность и жесткость. Принять . Данные своего варианта взять из табл. 5. Окончательно принимаемое значения диаметра вала должно быть округлено до ближайшего большего четного или оканчивающегося на пять числа.

Задачи 91 – 100. Для стальной балки, жестко защемленной одним концом и нагруженной, как показано на рис. 14 (схемы 1 – 10), построить эпюры поперечных сил и изгибающих моментов и подобрать из условия прочности необходимый размер двутавра, приняв Данные своего варианта взять из табл. 6.

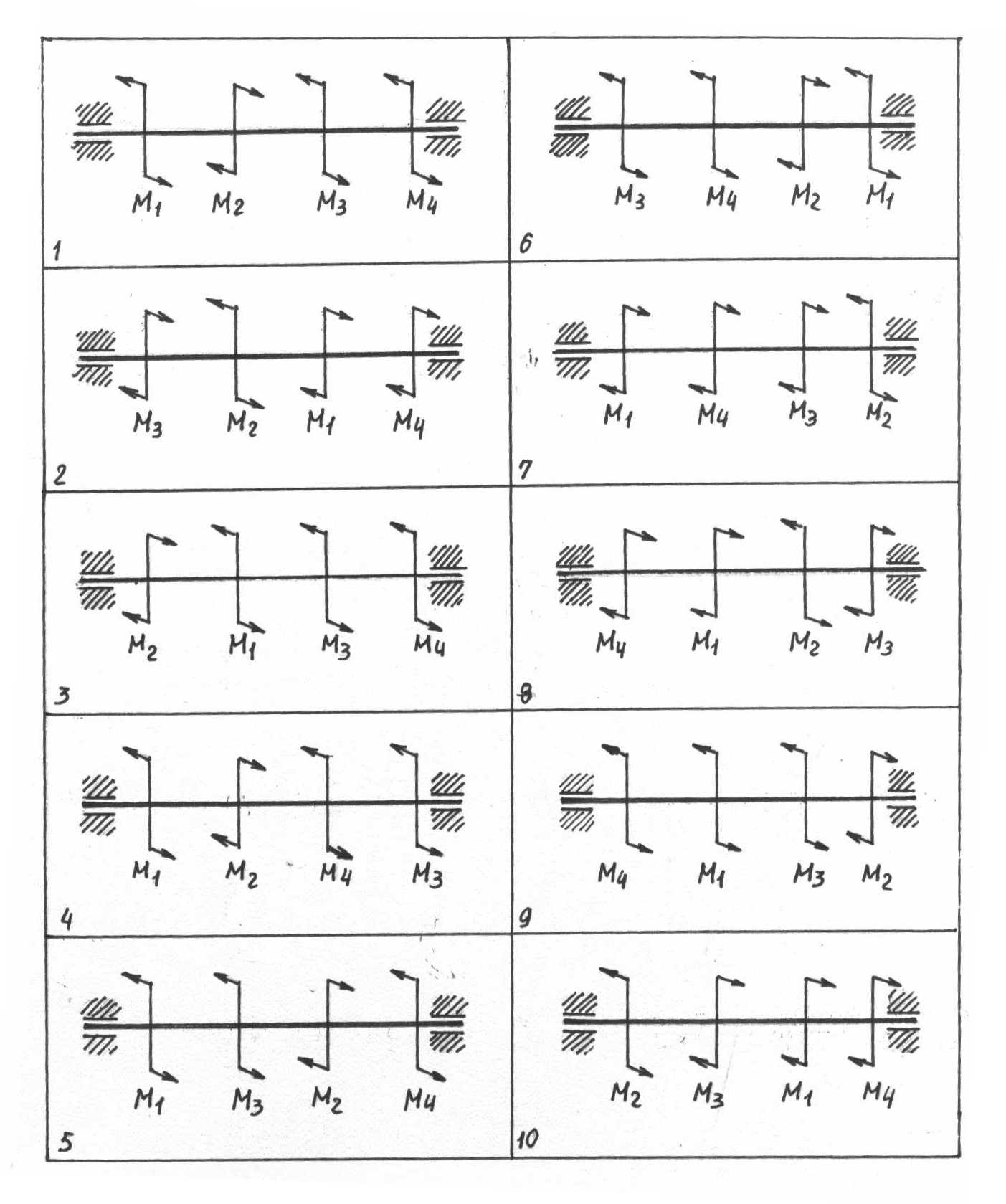
Рисунок 13.

Таблица 4 (к задачам 61-70)

№ задачи № схемы на рис.11	Вариант						№ задачи № схемы на рис.11	Вариант
		кН			см2				кН			см2
61; 1	00 11 21 31 49 58 63 71 81 91	30 16 17 14 27 24 18 26 36 32	10 15 13 16 14 11 12 13 20 16	5 10 8 11 8 6 5 7 12 9	1,8 1,1 1,0 1,2 1,7 1,5 1,6 1,7 2,5 1,0	3,2 18 2,2 1,9 3,1 2,9 2,8 3,1 4,0 2,2	62; 2	01 10 20 30 39 59 61 74 84 90	20 12 18 11 19 17 12 14 21 10	8 5 10 6 7 6 5 4 9 3,5	4 3 5 2 3 3 2,5 2 5,5 1,5	2,0 1,0 1,9 1,1 2,1 1,8 0,9 1,1 2,2 0,8	2,8 1,5 2,7 1,6 3,0 2,9 1,4 1,5 3,2 1,4
63; 3	02 12 23 33 42 56 62 70 80 93	16 8 15 9 18 20 10 12 17 11	25 13 24 14 27 29 15 16 26 16	28 14,5 29 16 31 33 18 19 30 20	1,2 0,6 1,3 0,8 1,6 1,9 0,9 1,0 1,5 1,2	3,8 2,1 3,9 2,4 4,1 4,5 2,5 2,7 4,0 2,9	64; 4	03 13 22 32 41 57 60 77 87 92	26 14 24 16 27 25 15 18 29 31	9 5 10 7 10 11 6 8 12 14	3 1,5 3,5 2,5 4 4 2 3,5 6 8	1,9 1,0 2,0 1,1 2,1 2,0 0,9 0,8 2,2 2,4	1,6 0,7 1,7 0,9 1,8 1,8 0,6 0,5 1,9 2,0
65; 5	05 15 25 35 44 54 67 73 83 95	14 17 20 13 18 22 15 10 23 12	16 19 18 17 20 19 18 14 21 15	10 13 12 9 14 13 12 11 15 9	2,1 2,4 2,5 2,0 2,3 2,4 2,0 0,9 2,1 1,9	1,9 2,1 2,2 1,7 1,9 2,1 1,8 0,7 1,8 1,7	66; 6	04 14 24 34 43 55 65 76 86 94	28 19 26 20 30 18 29 25 21 31	22 14 20 15 23 15 21 19 15 24	12 4 10 6 14 5 10 8 4 15	4,8 2,9 4,6 3,0 5,1 3,2 4,7 4,5 3,4 5,0	2,6 1,8 2,4 2,1 2,9 1,6 2,4 2,1 1,8 2,6
67; 7	07 17 27 37 46 52	17 20 14 19 12 21	13 17 10 15 8 18	8 10 6 7 4 9	2 2,2 1,7 2,1 1,6 2,3	2,5 2,7 2,3 2,6 2,2 2,8	68; 8	06 16 26 36 45 53	10 17 9 20 8 19	12 19 11 22 10 21	13 20 12 24 12 24	0,9 1,6 1,0 2,1 0,6 1,8	0,7 1,4 0,8 1,9 0,4 1,6

Продолжение таблицы 4

№ задачи № схемы на рис.11	Вариант						№ задачи № схемы на рис.11	Вариант
		кН			см2				кН			см2
	66 72 82 97	15 18 23 16	11 14 19 12	7 6 10 5	1,8 1,9 2,2 1,8	2,4 2,5 2,7 2,3		64 79 89 96	10 15 22 8	12 18 24 11	15 20 27 15	1,0 1,2 2,1 0,7	0,8 1,0 1,9 0,5
69; 9	09 19 29 38 48 50 68 75 85 99	40 31 25 38 27 42 22 45 24 32	55 46 41 53 43 57 39 59 40 45	24 20 18 22 24 25 16 19 17 18	2,8 1,9 1,6 2,6 2,0 3,0 1,4 2,8 1,8 2,0	3,4 2,5 2,1 3,2 2,6 3,5 2,0 3,5 2,7 2,7	70; 10	08 18 28 40 47 51 69 78 88 98	29 15 30 18 30 14 32 28 10 35	2 1,1 4 1,3 3 1,0 6 1,5 0,5 5	54 34 56 37 58 37 60 51 35 57	1,9 0,8 2,0 0,7 2,0 0,9 2,2 1,8 0,6 2,3	1,4 0,5 1,5 0,4 1,6 0,6 1,8 1,3 0,3 1,7

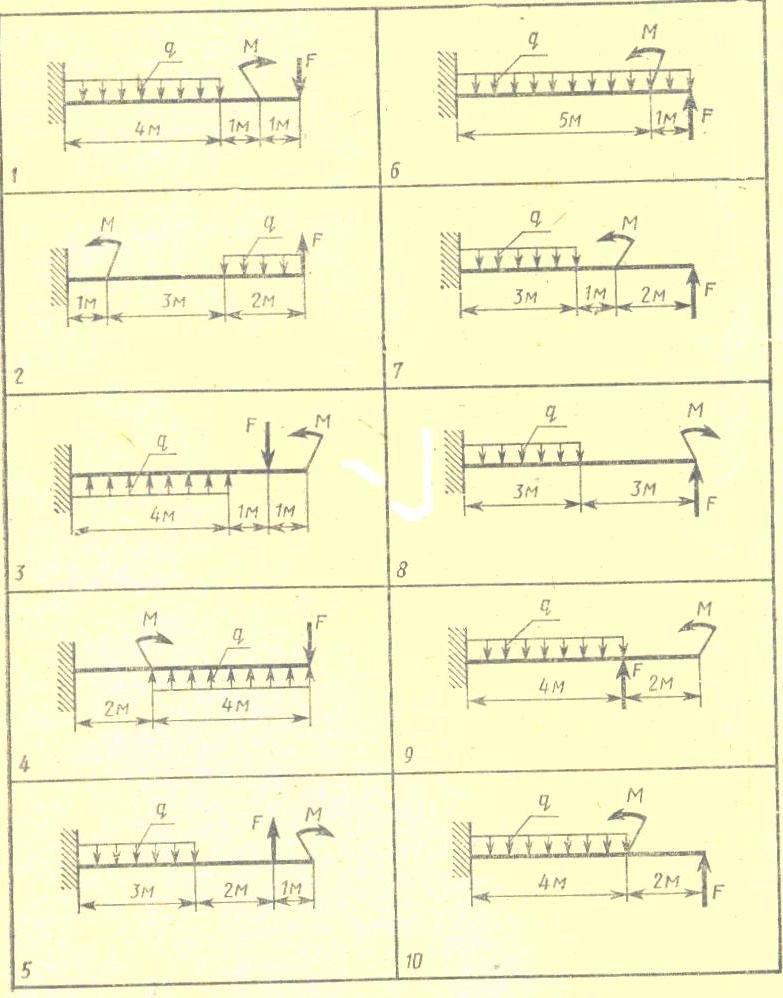
Рисунок 14

Таблица 5

№ задачи № схемы на рис.13	Вариант				, рад/с	№ задачи № схемы на рис.13	Вариант				, рад/с
		кВт						кВт
81; 1	00 12 25 30 41 52 68 71 82 99	35 150 40 110 40 75 90 65 140 120	20 100 25 60 15 40 60 35 110 80	15 50 20 30 25 15 25 20 60 40	20 45 25 35 30 20 30 25 45 35	82; 2	01 1 24 33 44 55 69 70 89 98	130 100 90 120 80 110 85 72 75 120	90 65 45 30 55 50 45 54 60 40	40 25 20 30 35 40 40 36 45 20	45 35 20 20 25 20 30 18 15 20
83; 3	02 15 27 32 43 54 66 73 85 91	15 75 55 45 80 50 70 55 65 40	10 80 65 50 65 40 60 40 55 30	35 25 25 35 45 30 40 18 35 30	16 40 20 23 30 18 25 32 35 16	84; 4	03 14 26 35 46 57 67 72 88 90	60 150 95 110 130 70 85 100 90 140	40 100 70 85 90 45 50 65 70 110	20 75 45 50 55 30 25 30 35 50	20 55 35 300 40 18 20 25 25 45
85; 5	05 17 29 34 45 56 64 75 81 93	100 50 40 100 90 30 5 110 80 95	18 15 120 80 25 100 95 20 50 45	50 25 20 65 40 25 20 60 35 20	20 18 20 25 20 30 25 15 25 18	86; 6	04 16 28 37 48 59 65 74 84 92	60 45 50 20 15 35 80 25 35 45	150 100 110 85 65 90 130 80 95 120	80 60 75 35 25 45 90 40 50 60	55 30 30 20 15 20 45 18 20 30

Продолжение таблицы 5

№ задачи № схемы на рис.13	Вариант				, рад/с	№ задачи № схемы на рис.13	Вариант				, рад/с
		кВт						кВт
87; 7	07 19 21 36 47 58 62 77 80 95	18 16 20 60 35 16 80 32 24 30	35 30 35 90 50 30 100 50 38 55	40 45 100 120 80 35 150 110 55 70	10 12 25 45 40 12 50 40 18 25	88; 8	06 18 20 38 49 51 63 79 87 94	20 40 65 18 70 18 20 60 30 40	50 115 140 40 150 60 65 120 100 110	30 55 80 25 95 42 38 65 45 50	10 16 35 8 40 12 10 40 15 18
89; 9	09 11 23 39 40 50 60 76 83 97	52 30 35 50 65 75 25 42 50 24	100 80 95 120 160 150 60 75 110 50	60 45 50 65 80 95 42 50 75 38	32 15 18 20 30 30 10 15 22 9	90; 10	08 10 22 31 42 53 61 78 86 96	80 75 42 35 58 50 45 32 18 16	95 120 60 75 100 130 150 50 55 35	75 90 55 40 86 95 70 42 30 20	25 30 18 20 25 30 40 14 8 7

Таблица 6

№ задачи № схемы на рис.15	Вариант				№ задачи № схемы на рис.15	Вариант
		кН	кН∙м				кН	кН∙м
91; 1	00 13 27 33 41 59 64 73 85 96	20 30 40 50 60 80 80 90 90 90	10 20 10 10 10 10 20 20 20 30	10 20 20 20 20 30 40 40 50 60	92; 2	01 15 26 32 42 51 65 77 88 99	10 30 40 40 50 60 70 80 90 70	40 30 30 30 30 30 30 30 30 30	10 20 20 30 30 40 40 50 50 50
93; 3	02 14 29 35 49 53 62 74 82 98	20 30 10 10 20 30 40 50 50 60	10 10 10 10 10 10 10 10 10 10	10 10 10 20 20 20 20 20 30 30	94; 4	03 17 28 34 40 52 63 72 86 91	20 30 40 50 60 30 60 70 80 90	10 10 10 10 10 10 10 10 10 10	10 10 20 20 20 30 30 30 30 30
95; 5	05 16 21 37 44 50 60 70 83 90	10 10 20 30 40 50 20 30 40 40	10 10 10 10 10 10 10 10 10 10	10 20 20 20 20 20 30 30 30 40	96; 6	04 19 20 36 43 54 61 78 89 93	30 40 50 50 60 70 80 90 80 90	10 10 10 10 10 10 10 10 10 10	10 10 10 20 20 20 20 20 30 30

Продолжение таблицы 6

№ задачи № схемы на рис.15	Вариант				№ задачи № схемы на рис.15	Вариант
		кН	кН∙м				кН	кН∙м
95; 5	05 16 21 37 44 50 60 70 83 70	10 10 20 30 40 50 20 30 40 40	10 10 10 10 10 10 10 10 10 10	10 20 20 20 20 20 30 30 30 40	96; 6	04 19 20 36 43 54 61 78 89 93	30 40 50 50 60 70 80 90 80 90	10 10 10 10 10 10 10 10 10 10	10 10 10 20 20 20 20 20 30 30
97; 7	07 18 23 38 46 55 67 79 81 92	10 20 20 30 40 40 50 30 20 50	10 10 10 10 10 10 10 10 10 10	10 10 20 20 20 30 30 30 30 40	98; 8	06 11 22 30 45 56 66 75 84 95	10 20 20 30 40 40 50 50 60 80	10 10 20 20 20 20 20 20 20 20	10 10 20 20 20 30 40 30 30 40
99; 9	09 10 25 31 48 57 69 76 80 94	20 30 30 40 50 50 60 70 50 60	10 10 10 10 10 10 10 10 10 10	10 10 20 20 20 30 30 30 40 40	100; 10	08 12 24 39 47 58 68 71 87 97	10 20 30 30 20 40 40 50 50 60	10 10 10 10 10 10 10 10 10 10	10 10 10 20 20 20 30 30 40 40

КРИТЕРИИ ОЦЕНКИ

Отметка в баллах	Показатели оценки
1 (один)	Узнает отдельные термины, явления, определения, величины, детали, сборочные единицы, соединения, передачи и т.п.
2 (два)	Различает термины, определения, механические явления и величины, детали, сборочные единицы, соединения, передачи, виды нагрузок и деформаций. Конспектирует дословно излагаемый материал. Выпол­няет отдельные действия по указанию преподавателя в практических и лабораторных работах.
3 (три)	Дает неполные определения отдельных теорем, величин, понятий, яв­лений, в том числе с подсказкой и своими словами. Выполняет реше­ние задач, лабораторных и др. работ по образцу.
4 (четыре)	Недостаточно осознанно воспроизводит большую часть теоретическо­го материала по программе. Знает основные законы (Ньютона, Гука, Амонтона-Кулона) и теоремы механики. Производит сложение сил и моментов, определяет реакции связей, знает основные законы движе­ния точки и твердого тела, принципы расчета на прочность и жест­кость при растяжении (сжатии), кручении, сдвиге, изгибе (поперечном, чистом, продольном), переменных нагрузках и решает соответствую­щие задачи по образцу. Дает общую характеристику изучаемых пере­дач, соединений, деталей и сборочных единиц. При этом делает еди­ничные существенные ошибки.
5 (пять)	Осознанно воспроизводит большую часть теоретического материала по программе. Знает основные законы и теоремы механики. Произво­дит сложение сил и моментов, определяет реакции связей, знает ос­новные законы движения точки и твердого тела, принципы расчета на прочность и жесткость при растяжении (сжатии), кручении, сдвиге, изгибе (поперечном, чистом, продольном), переменных нагрузках и решает соответствующие задачи по образцу. Характеризует все изу­чаемые передачи, соединения и сборочные единицы. Однако при этом допускает несущественные ошибки.
6 (шесть)	Демонстрирует полное знание и осознанное воспроизведение всего программного учебного материала. Владеет программным учебным материалом в знакомой ситуации: описывает и объясняет объекты изучения каждой темы, выявляет и обосновывает закономерные связи между механическими явлениями и величинами, приводит примеры из практики, в том числе в области автомобильной техники, выполняет упражнения, задачи и задания по соответствующим темам учебной программы по образцу, на основе предписаний. Допускает несущест­венные ошибки.
7 (семь)	Демонстрирует полное, прочное знание и воспроизведение всего про­граммного учебного материала. Владеет программным учебным мате­риалом в знакомой ситуации: дает развернутое описание и объяснение объектов изучения каждой темы, раскрывает сущность механических явлений и процессов, обосновывает связи и закономерности, приводит доказательства теоретических положений и выводов, формулирует вы­воды по изучаемой теме, выполняет соответствующие практические задания (недостаточно самостоятельно). Допускает единичные несущественные ошибки

8 (восемь)	Демонстрирует полное, прочное, глубокое знание и воспроизведение всего программного учебного материала Оперирует программным учебным материалом в знакомой ситуации: дает развернутое описание и объяснение объектов изучения каждой темы, раскрывает сущность механических явлений и процессов, обосновывает связи и закономер­ности, приводит доказательства теоретических положений и выводов, подтверждает положения и выводы соответствующими аргументами и фактами, формулирует выводы по изучаемой теме, выполняет само­стоятельно практические задания. Допускает единичные несуществен­ные ошибки.
9 (девять)	Демонстрирует полное, прочное, глубокое, системное знание всего программного учебного материала. Оперирует программным учебным материалом в частично измененной ситуации: применяет учебный ма­териал на основе известных правил, предписаний, а также осуществля­ет поиск нового знания, новых закономерностей, способов решения задач, выдвигает свои предположения и гипотезы. Анализирует мате­риал, прогнозирует те или иные связи, положения, проявляет творче­ство и рационализм, свободно пользуется справочной литературой, выбирает способы выполнения практических заданий.
10 (десять)	Свободно оперирует программным учебным материалом. Применяет знания и умения в незнакомой ситуации: самостоятельно производит действия по описанию, объяснению объектов изучения каждой темы, формулированию правил, построению алгоритмов для выполнения практических заданий, демонстрирует рациональные способы решения задач, выполняет творческие работы и задания повышенной сложно­сти, в том числе для студентов вузов.

36