2.4. Виды погрешностей
Все первичные (элементарные) погрешности обработки можно разделить на систематические постоянные, систематические переменные и случайные.
Систематическими постоянными погрешностями называют такие, которые при обработке партии заготовок постоянны по значению и знаку. Систематическая постоянная погрешность появляется, например, вследствие погрешности в размере режущего инструмента (зенкера, развертки и др.) или в результате неточности профиля фасонного резца, протяжки и др.
Систематическими переменными погрешностями называют такие, которые в процессе обработки закономерно изменяются по времени, т. е. в зависимости от числа изготовленных изделий. К этой группе относится погрешность, вызываемая износом режущего инструмента, и погрешность, обусловленная тепловыми деформациями элементов технологической системы в период работы станка.
Случайными погрешностями называют такие, которые для заготовок данной партии имеют различные значения, причем появление таких погрешностей и точное их значение заранее предсказать невозможно. К случайным погрешностям относятся погрешность установки заготовки, погрешность установки режущего инструмента при наладке станка, погрешность, обусловленная упругими смещениями элементов технологической системы. Например, изменения значений упругих смещений элементов зависят от неравномерной твердости заготовок, от колебаний припуска на обработку, которые носят случайный характер.
2.5. Вероятностно-статистический метод оценки точности [2]
Этот
метод основан на проведении обработки
опытной партии заготовок с измерением
интересующего размера шкальным
инструментом (микрометром или другим
в зависимости от требуемой точности
измерений). Результаты измерений
математически обрабатывают, после чего
строят кривую распределения исследуемого
размера. Для этого в полученном ряде
размеров выявляют предельные значения.
Разность
между наибольшим
и
наименьшим
действительными размерами заготовок
в данной партии называют размахом
распределения или полем рассеяния
размеров:
=
(2.1)
Полученное значение разбивают на равные интервалы и определяют частость повторения отклонений размеров в каждом интервале:
, (2.2)
где m число заготовок, фактический размер которых находится в пределах данного интервала; n общее число деталей в партии.
Далее
строят график (полигон) распределения
размеров. По оси абсцисс откладывают
фактические размеры заготовок (или
интервалы размеров), а по оси ординат
частость их повторения w.
Например, для графика, приведенного на
рис. 2.1, а, общее число деталей в исследуемой
партии составляет 100 шт. Поле рассеяния
размеров
= 0,16 мм. Для построения полигона размеров
принято восемь размерных групп с
интервалом в 0,02 мм. В первой размерной
группе оказалось 5 деталей, т. е. частость
=
0,05, во второй группе
13, т. е. частость
= 0,13, и т. д. Полученные точки соединяют
прямыми.
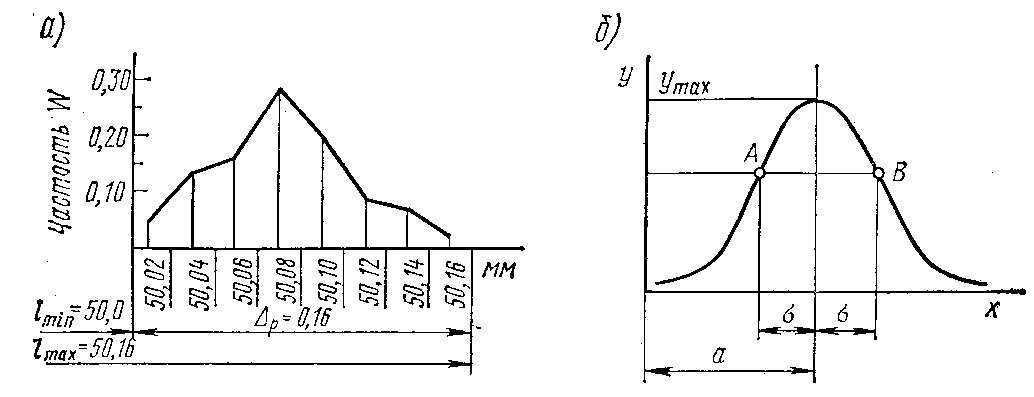
Рис. 2.1. Кривые распределения: а – полигон распределения; б – кривая нормального распределения
Если увеличить число размерных групп (например, принять интервал в 0,01 мм) и увеличить общее число обрабатываемых деталей, то ломаная линия становится более плавной.
Экспериментально установлено, что при обработке заготовок на металлорежущих станках способом автоматического получения размеров точность обработки подчиняется в большей или меньшей степени закону нормального распределения, который изображается математической кривой Гаусса (рис. 2.1, б), уравнение которой
y=
, (2.3)
где σ среднее квадратичное отклонение аргумента; е основание натуральных логарифмов; параметр а является центром группирования значения аргумента и в то же время его средней арифметической.
Среднее квадратичное отклонение σ определяют по результатам измерений партии заготовок по формуле
=
(2.4)
где n
число произведенных измерений;
значение текущего измерения; х
среднее арифметическое данных измерений:
=
(2.5)
Число измерений n следует брать 50 или более. При меньшем значении n погрешность определения σ превышает ± 10 %.
Кривая
нормального распределения симметрична.
Ордината вершины кривой
будет при х
=
а;
она определяется из выражения
=
(2.6)
Кривая имеет точки перегиба на расстояниях х = ± Их ординаты равны:
=
=
0,6
. (2.7)
Величина
характеризует
форму кривой распределения и является
мерой точности данного метода обработки;
при увеличении
вершина кривой снижается, но ветви
кривой растягиваются, т. е. поле рассеяния
размеров растет. При уменьшении
ордината
кривой возрастает, а поле рассеяния
сужается. На рис. 2.2, а
схематически
показаны кривые распределения
диаметральных размеров при обработке
партии заготовок последовательно после
предварительного точения (кривая
),
чистового точения (кривая
)
и
шлифования (кривая
),
причем при правильном построении этапов
процессов необходимо выполнение условия
>
>
.
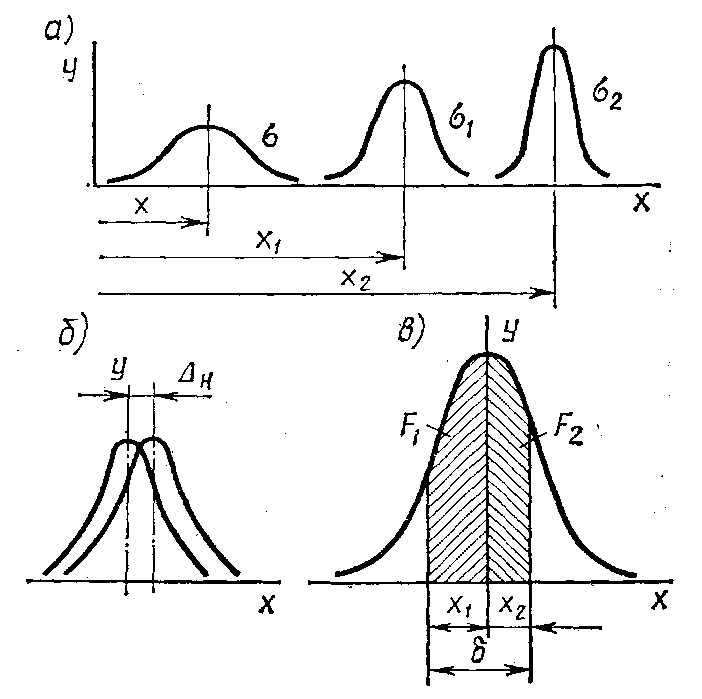
Рис. 2.2. Анализ точности обработки с помощью кривых распределения
Если
обрабатываются две партии одноименных
заготовок, то появляется систематическая
постоянная погрешность, связанная с
погрешностью настройки станка на размер
или с различными отклонениями размеров
режущего инструмента. В этом случае
кривые распределения погрешностей при
обработке первой и второй партий будут
смещены одна относительно другой на
размер постоянной погрешности
(рис. 2.2, б).
Изучение
кривых распределения погрешностей
позволяет выявить соотношение между
числом годных и бракованных деталей.
Предположим, что на обработку заготовок
установлен допуск δ. На оси абсцисс
(рис. 2.2, в)
этот
допуск определяется величинами
и
от
положения центра группирования.
Заштрихованный участок соответствует
числу заготовок, находящихся в пределах
поля допуска. Отношение площади этого
участка к общей площади, ограниченной
кривой, определяет вероятность получения
годных заготовок, так как площадь,
ограниченная кривой нормального
распределения, соответствует общему
числу заготовок в партии.
Площади
и
рассчитывают по формулам:
. (2.8)
При изучении точности обработки кроме закона нормального распределения (закон Гаусса) встречаются и другие законы распределения размеров. Если размер обработки зависит только от действия одного фактора, изменяющегося по закону прямой, то распределение размеров подчиняется закону равной вероятности. Например, в верхней части рис. 2.3, а показано, что возрастание размера х обработанной поверхности в результате постепенного износа режущего инструмента происходит по закону прямой х = аτ, где τ время резания, а постоянная величина, характеризующая интенсивность изнашивания резца; в нижней части этого рисунка приведена кривая распределения размеров в виде прямоугольника, соответствующая закону равной вероятности.
В том случае, когда размер х интенсивно возрастает в начальный период резания, затем его рост замедляется и вновь увеличивается (в конце стойкости режущего инструмента), что показано в верхней части рис. 2.3, б, кривая распределения размеров, показанная в нижней части этого рисунка, соответствует закону треугольника (закону Симпсона).
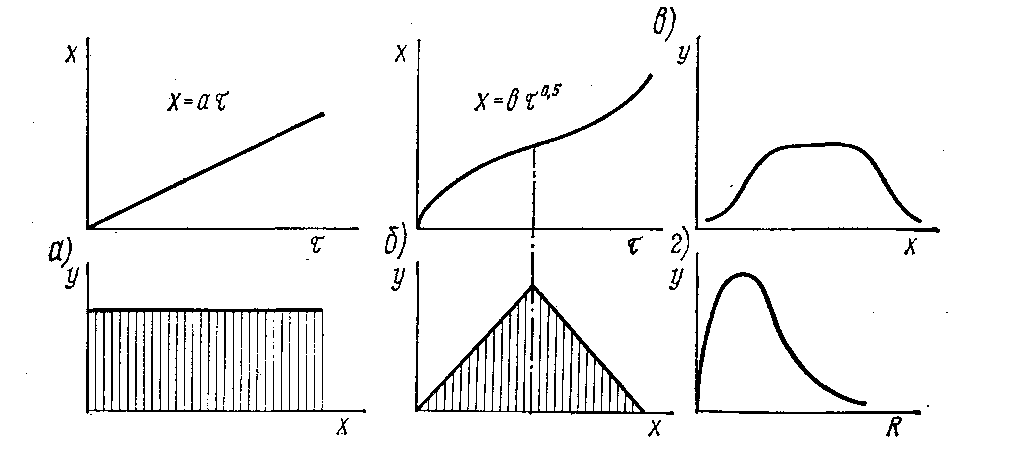
Рис. 2.3. Разновидности кривых распределения
В случае совместного влияния на точность обработки закономерно изменяющейся погрешности, например, износа режущего инструмента, подчиняющегося закону равной вероятности, и случайных погрешностей, подчиняющихся закону Гаусса, кривая распределения искажается. На рис. 2.3, в в качестве примера показана композиция кривой Гаусса и кривой равной вероятности.
Рассеяние значений эксцентриситета, биения, дисбаланса и т. п. подчиняется закону Максвелла. Эти погрешности являются положительными величинами, изменяясь от нуля до определенного значения. На рис. 2.3, г показана кривая распределения эксцентриситетов ступенчатых валов. Форма этой кривой несимметричная.
Метод оценки точности на основе кривых распределения универсален и позволяет объективно оценить точность механической обработки, сборочных, контрольных и других операций. Недостаток метода невозможность выявить изменение изучаемого параметра во времени, т. е. последовательности обработки заготовок, что не позволяет осуществить регулирование хода технологического процесса. Кроме того, переменные систематические погрешности нельзя отделить от случайных; это затрудняет выявление и устранение причин погрешностей.