5. Интервал между событиями. Пространство Минковского. 4-векторы. 4-скорость, 4-импульс. Закон сохранения энергии-импульса.

Л юбое событие определяется местом (совокупностью координат x, y, z) и моментом времени, когда оно произошло. Пусть в инерциальной системе отсчета К произошли два события А(x,y,z,t) B(x+dx,y+dy,z+dz,t+dt). Интервалом между событиями называется величина, квадрат которой в системе К равен:

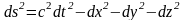. (1)

В системе К^/ квадрат интервала между этими же событиями:

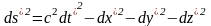. (2)

Покажем, что 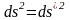. Т.к. dy=dy ^/, dz=dz^/, то надо доказать

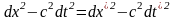. (3)

Используя обратные преобразования Лоренца:

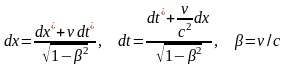(4)

получим соотношение (3). Итак, при переходе от системы К к системе К^/ квадрат интервала является инвариантом.

В СТО трехмерное пространство и время объединяются в одно четырехмерное пространство, которое называют пространством Минковского. События в пространстве Минковского называют мировыми точками, а линии в этом пространстве – мировыми линиями. Участки мировых линий, вдоль которых ds² >0 называются времениподобными, при ds² = 0 светоподобными, при ds² <0 – пространственноподобными.

Опр. Собственным временем частицы называется время, измеренное по часам, связанным с движущейся частицей.

Пусть в системе К скорость частицы 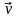. В этой системе приращения координат и времени обозначим dx, dy, dz, dt. Пусть в системе К^/ эта частица покоится, тогда для нее приращение координат и времени будут: 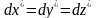=0, d. Запишем инвариантное значение квадрата интервала:

,

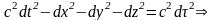
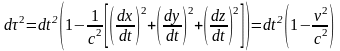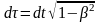(5)

В четырехмерном пространстве определим координаты события

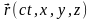– 4 радиус-вектор, приращение 4 радиус-вектора: 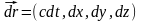. Более компактная запись: , .

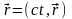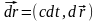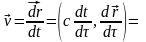
4-скорость определим следующим образом: 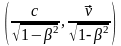. В СТО масса покоя частицы m₀ является инвариантной величиной. По аналогии с классической механикой определим 4-импульс как

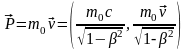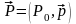. Сокращенная запись: , где 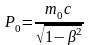, – релятивистский трехмерный импульс. Вычислим выражение .

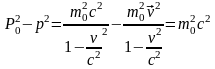Т.е. 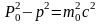является инвариантом. (6)

В СТО энергия тела определяется как величина, равная

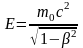. (7)

Каждое тело в состоянии покоя (v=0) обладает энергией 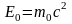. Отметим, что это очень большая энергия. Например, тело массой 1 кг обладает энергией покоя Е₀ =1 кг(310⁸ м/с)² =910¹⁶ Дж.

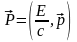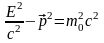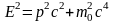Учитывая соотношение (7) и выражение для Р₀, выражение для 4-импульса запишем в виде: . С учетом этой записи инвариант (6) будет иметь вид: или . (8)

(8) является главной прикладной формулой СТО, она заменяет ньютоновскую формулу, связывающую кинетическую энергию с импульсом: E_кин = 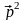/(2m). Из формулы Эйнштейна следует, что при 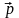= 0 E₀ = m₀c². Смысл этой знаменитой формулы в том, что массивная частица обладает определенной энергией покоя Е₀, однозначно связанной с массой этой частицы. Эйнштейн постулировал, что эта энергия вполне реальна и при изменении массы частицы может переходить в другие виды энергии и это является основой ядерных реакций. Соотношение Эйнштейна выражает всеобщий закон эквивалентности и взаимопревращения массы и энергии.

6. Уравнения Максвелла для системы зарядов в вакууме, их физический смысл.

Система уравнений Максвелла – основа электродинамики и является обобщением экспериментальных данных. Уравнения Максвелла записывают в интегральной и дифференциальной форме.

Дифференциальная форма Интегральная форма

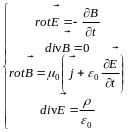
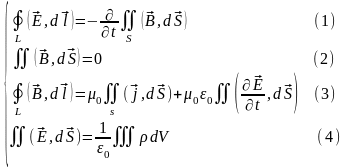
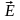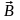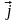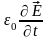где – напряженность электрического поля, – вектор индукции магнитного поля, – плотность токов проводимости, – плотность токов смещения, – плотность зарядов. В уравнения входят константы ₀ =410^–7Вс/(Ам) – магнитная постоянная, ₀= 8,8510^–12 Ф/м – электрическая постоянная.

Уравнения (1) – (4) устанавливают связь между векторами электромагнитного поля, плотностью зарядов и плотностью токов в любой точке пространства в любой момент времени.

Дифференциальная форма уравнений позволяет рассчитать электромагнитное поле по распределению зарядов и токов в пространстве. Но это достаточно сложная задача с точки зрения математики, поэтому часто при решении конкретных задач используют интегральную форму. Кроме того, интегральная форма нагляднее физически.

Для примера рассмотрим дифференциальное уравнение (4). Выделим в пространстве некоторый объем V, ограниченный поверхностью S. Пусть внутри объема находятся заряды, распределенные с плотностью . Проинтегрируем данное уравнение по объему V:

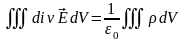(5)

Применим к левой части (5) теорему Остроградского:

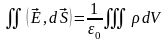(6)

Интеграл 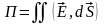определяет поток вектора напряженности через поверхность S, окружающую заряд 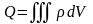Соотношение (6) называют теоремой Гаусса.

Для наглядности поле вектора изображают с помощью силовых линий. Число линий, пересекающих поверхность, перпендикулярную к ним, равно потоку П вектора напряженности .

Физический смысл уравнений (4). Источниками электрического поля являются электрические заряды. Поток вектора напряженности электрического поля через замкнутую поверхность S определяется суммарным электрическим зарядом, находящимся внутри данной поверхности. С уравнениями (4) связан закон Кулона.

Уравнения (1) связаны с законом Фарадея для электромагнитной индукции. Физический смысл уравнений: вихревое электрическое поле порождается переменным магнитным полем. Величина 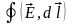определяет э.д.с индукции, а 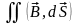– поток вектора магнитной индукции через поверхность S. Э.д.с. индукции, возникающая в замкнутом проводнике L, определяется изменяющимся магнитны потоком, пронизывающим контур проводника.

Уравнения (2) показывают, что отсутствуют магнитные заряды и силовые линии магнитного поля всегда замкнуты. Сколько силовых линий выходит из объема V, столько и заходит в этот объем. Можно также сказать, что силовые линии магнитного поля либо замкнуты, либо приходят из бесконечности и уходят на бесконечность.

В уравнениях (3) , – плотности токов проводимости и токов смещения, а и 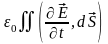– токи проводимости и токи смещения, + – полный ток. Физический смысл уравнений (3): вихревое магнитное поле порождается полным током.

Уравнения Максвелла (1)-(4) применимы для исследования потоков элементарных частиц или ионов в пустоте (например, плазма, ионные пучки). В ряде случаев, когда окружающие тела не влияют на электромагнитное поле, данные уравнения применяют и для расчета полей в веществе. Например, поле малых заряженных тел в воздухе рассчитывается как поле точечных зарядов в вакууме, магнитное поле линейного проводника с током – как поле тока в вакууме.

Из уравнений Максвелла выводится ряд фундаментальных законов и следствий, подтверждаемых экспериментом, например, закон сохранения заряда, закон сохранения энергии и импульса электромагнитного поля и т.д.

Покажем, как закон сохранения заряда получается из уравнений Максвелла.

Вычислим дивергенцию от обеих частей уравнения (3), при этом используем свойство цикличности перестановок в смешанном произведении: 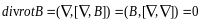, тогда 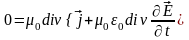или

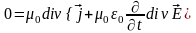(7)

Подставив в (7) (4), получим закон сохранения заряда в дифференциальной форме:

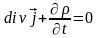(8).