4. Экспериментальные основания сто. Постулаты Эйнштейна. Преобразования Лоренца и их кинематические следствия.

Классическая механика основывалась на двух фундаментальных принципах:

1) все инерциальные системы отсчета равноправны, т.е. любое механическое явление протекает одинаково во всех инерциальных системах;

2) взаимодействия между телами распространяются мгновенно, т.е. возможны любые значения скорости распространения, вплоть до бесконечно больших.

Во второй половине ХIХ века стали бурно развиваться оптика и электродинамика, которые подтвердили выполнение первого принципа не только для механических, но и электромагнитных процессов и опровергли второй принцип для случая распространения электромагнитных волн. В 1676 г. Рёмер впервые измерил скорость света. Наблюдения затмений спутников Юпитера показали, что наблюдаемый период их обращения уменьшается, когда Земля приближается к Юпитеру, и увеличивается, когда Земля удаляется от него. Рёмер понял, что этот эффект является следствием конечной скорости света и измерил эту скорость. Он получил результат, близкий к современному. В 1860 году Физо поставил опыт по измерению скорости света в движущейся среде. Один из лучей света двигался по течению жидкости, другой – против. Результатом опыта был вывод, что скорость света и скорость течения жидкости не складываются по законам классической механики. После работ Юнга, установившего принцип интерференции и работ Френеля по теории дифракции в оптике прочно установилась волновая теория света, согласно которой свет как волна распространялся в неподвижном эфире. Скорость движения любого тела относительно эфира была названа абсолютной. Майкельсон попытался вычислить абсолютную скорость движения Земли относительно эфира. Идея опыта Майкельсона состояла в том, чтобы сравнить время прохождения светом двух путей, один из которых совпадает с направлением движения Земли в эфире, а другой ему перпендикулярен. Результатом этого опыта явилось доказательство отсутствия среды, названной эфиром, и был сделан вывод о независимости скорости распространения света от скорости движения источника света.

Все перечисленные эксперименты привели к пересмотру классических представлений и созданию специальной теории относительности.

Основу специальной теории относительности составляют два постулата:

1) все инерциальные системы отсчета равноправны, т.е. любое явление природы (не только механическое) протекает одинаково во всех инерциальных системах;

2) взаимодействия между телами распространяются с конечной скоростью. Максимальная скорость распространения физических сигналов (взаимодействий) не зависит от движения источника и совпадает со скоростью света в вакууме с = 310⁸м/с.

Физический процесс – это последовательность событий. Любое событие определяется местом (т.е. совокупностью координат x, y, z) и моментом времени, когда оно произошло.

Р ассмотрим две инерциальные системы отсчета К и К^/. Пусть система К^/ движется со скоростью v относительно неподвижной системы К.

Связь между координатами двух систем устанавливают преобразования Лоренца:

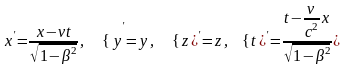, (1) где 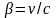. Если решить (1) относительно x,y,z, то получим обратные преобразования Лоренца:

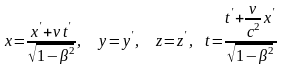(2)

Формулы (1) и (2) устанавливают связь между координатами одного и того же события в двух инерциальных системах отсчета. Из данных преобразований вытекают следующие следствия.

1. Разноместные одновременные события в системе К не являются таковыми в системе К^/.

Пусть в момент времени t в системе К произошли одновременно два события в точках х₁  х₂. Определим моменты времени этих событий в системе К^/, используя (1):

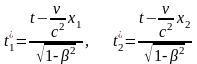так как х₁  х₂, то

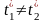
2. Относительность длины.

Пусть в системе К длина неподвижной линейки 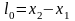, где х₁, х₂ – координаты концов линейки. В системе К^/ в момент времени t^/ измеряются координаты концов этой линейки и определяется её длина: 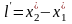. Этим координатам в системе К в соответствии с (2) отвечают значения:

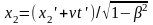, , тогда

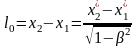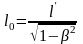или , т. е. 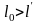– длина предмета в системе, где он покоится наибольшая. Длина предмета в системе, где он покоится, называется собственной длиной.

3. Относительность промежутков времени.

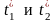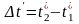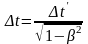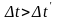Пусть в системе К^/ в неподвижной точке х^/ произошли события в моменты времени . Промежуток времени между ними: . В системе К эти события произошли в моменты времени . Интервал времени между событиями в системе К: , т.е. . Мы получили, что движущейся системе К^/ промежуток времени наименьший. Иногда этот результат выражают словами: в движущемся теле процессы замедляются.